FP

Funkcijsko programiranje

Author

RAPTOR_6

Funkcijsko programiranje

2024-25

Ultimate edition

RAPTOR_6

Vključuje:

predavanja (vse + koda s predavanj)
vaje (vse)
seminarske naloge (vse)
izpite in kolokvije (od 2024/25 1. rok pa do 2018/19 1. kolokvij: 12 skupaj)

Desno zgoraj je toggle za rešitve, da se jih lahko skrije.

1 Predavanja

Vsebina predmeta - uvod

Funkcijsko programiranje

SML:

uvod v Standardni ML
sestavljeni podatkovni tipi
konteksti spremenljivk
ujemanje vzorcev, gnezdenje vzorcev
funkcije višjega reda, map/reduce/filter
ovojnice, delne aplikacije, currying
skrivanje kode v programskih modulih

Racket:

zakasnjena evalvacija
memoizacija
uporaba makro sistema
močna/šibka, dinamična/statična tipizacija
implementacija interpreterja

Python:

funkcijsko programiranje v mešano-paradigemskem okolju?
primerjava z objektno-usmerjenim progr.

Snov

1.1 Uvod, funkcijsko programiranje, prvi koraki v SML

1.1.1 Funkcijsko programiranje

Algoritem - opis postopka za reševanje problema.

Načini opisovanja problemov v sodobnih programskih jezikih:

proceduralno: program je zaporedje navodil (C, Pascal, skriptni jeziki, Basic)
deklarativno: program je specifikacija, ki opiše problem; jezik izvede reševanje (SQL, Prolog)
objektno-usmerjeno: programi manipulirajo zbirke objektov s stanji in metodami (C++, Java, Python)
funkcijsko: program je zapisan kot zaporedje funkcij. Te imajo vhode in izhode, ne hranijo in spreminjajo pa notranjega ali globalnega stanja (spremenljivk) (Standardni ML, OCaml, Haskell, Lisp, Racket, Scheme, Clean, Mercury, Erlang).

Mešano-paradigemski jeziki (npr. Python, R, …).

Večji programi -> večja kompleksnost kode. Potreba po večji abstrakciji kode, izogibanje pretiranim podrobnostim.

Analogija - babičin recept:

Yes, dear, to make pea soup you will need split peas, the dry kind. And you have to soak them at least for a night, or you will have to cook them for hours and hours. I remember one time, when my dull son tried to make pea soup. Would you believe he hadn’t soaked the peas? We almost broke our teeth, all of us. Anyway, when you have soaked the peas, and you’ll want about a cup of them per person, and pay attention because they will expand a bit while they are soaking, so if you aren’t careful they will spill out of whatever you use to hold them, so also use plenty water to soak in, but as I said, about a cup of them, when they are dry, and after they are soaked you cook them in four cups of water per cup of dry peas. Let it simmer for two hours, which means you cover it and keep it barely cooking, and then add some diced onions, sliced celery stalk, and maybe a carrot or two and some ham. Let it all cook for a few minutes more, and it is ready to eat.

⬇️

Per person: one cup dried split peas, half a chopped onion, half a carrot, a celery stalk, and optionally ham.

Soak peas overnight, simmer them for two hours in four cups of water (per person), add vegetables and ham, and cook for ten more minutes.

1.1.1.1 Prvi koraki po abstrakciji

Ostanimo pri proceduralnem (imperativnem) programiranju

abstraktnejši pristop k programiranju,
zmanjšanje količine nepotrebnih podrobnosti z namenom povečanja preglednosti programa

Primer:

`def sestej1(stevila): i = 0 sum = 0 meja = len(stevila) while i < meja: sum += stevila[i] i += 1 return sum`	“Imamo neko spremenljivko i, ki začne šteti pri 0 in šteje do velikosti polja, ki mu rečemo meja, ter za vsako vrednost i poiščemo ustrezen element v seznamu stevila in ta element prištejemo skupni vsoti…”
`def sestej2(stevila): sum = 0 for x in stevila: sum += x return sum`	“Za vsak element seznama števila prištej ta element k skupni vsoti”

Želimo iti še dlje? DA! Funkcijsko programiranje:

zapis programa kot evalvacija matematičnih funkcij,
fokus: KAJ izračunati namesto KAKO izračunati

1.1.1.2 Funkcijsko programiranje - jezik

Lastnosti funkcijskih jezikov:

funkcije so objekti
podpora funkcijam višjega reda (funkcije, ki se izvajajo na funkcijah, ki se izvajajo na funkcijah, ki se izvajajo na …)
uporaba rekurzije namesto zank
poudarek na delu s seznami
izogibanje “stranskim učinkom” programa (spreminjanje globalnega stanja, lokalne spremenljivke)
- do največjega deleža programskih napak pridemo, kadar spremenljivke med izvajanjem programa dobijo nepričakovane vrednosti. Rešitev: Izognimo se prirejanjem!

Prednosti funkcijskih programov:

lažji formalni dokaz pravilnosti programa
idempotentne funkcije (ne spreminjajo stanja po večkratni zaporedni uporabi) -> lažje testiranje (unit test) in razhroščevanje
ni definiran vrsti red evalvacije funkcij, možna lena (pozna) evalvacija (lazy evaluation)
sočasno procesiranje -> boljša paralelizacija
pomagajo boljše razumeti programerske stile

1.1.2 Standardni ML

Jezik ML: uporabljali bomo SML/NJ (Standard ML of New Jersey) http://www.smlnj.org/.

Program v ML:

REPL - Read-Eval-Print Loop: branje-evalvacija-izpis rezultatov, ki se izvaja v zanki
SML ni interpreter, temveč prevajalnik. REPL torej v ozadju prevede vsak ukaz v strojno kodo

Preprosti izrazi:

- (* jaz sem komentar *)
- 12;       (* celoštevilska vrednost *)
- true;     (* logična vrednost *)
- 3.14;     (* realna vrednost *)

1.1.2.1 Sintaksa in semantika

SINTAKSA = kako program pravilno zapišemo

SEMANTIKA = kaj program pomeni:

preverba pravilnosti podatkovnih tipov, angl. type-checking (pred izvajanjem)
evalvacija - izračun vrednosti (med izvajanjem)

ML preverja semantiko z uporabo statičnega in dinamičnega okolja:

statično okolje hrani podatke o programu, potrebne za preverjanje njegove pravilnosti pred izvajanjem. Hrani npr. podatkovne tipe obstoječih spremenljivk.
dinamično okolje hrani podatke o programu, ki so potrebne za preverjanje pravilnosti med izvajanjem. To so npr. vrednosti obstoječih spremenljivk.

Poglejmo si primere…

val x = 3;
(* staticno okolje: x -> int *)
(* dinamicno okolje: x -> 3 *)

val y = 5;
(* staticno okolje: y -> int, x -> int *)
(* dinamicno okolje: y -> 5, x -> 3 *)

val z = x + y;
(* staticno okolje: z -> int, y -> int, x -> int *)
(* dinamicno okolje: z -> 8, y -> 5, x -> 3 *)

val uspesno = if z > 5 then true else false;
(* staticno okolje: uspesno -> bool, ... *)
(* dinamicno okolje: uspesno -> true, ... *)

1.1.2.1.1 Vezava spremenljivk

V splošnem:

val 𝘅 = 𝗲

x je spremenljivka:

sintaksa: zaporedje črk, številk in znakov _, ki se ne prične s številko
pravilnost tipa: preveri, ali je že prisotna v statičnem okolju
evalvacija: preberi vrednost iz dinamičnega okolja

e je izraz:

sintaksa: vrednost ali sestavljeni izraz
semantika: vsaka vrednost ima svoj “vgrajeni tip” in se evalvira sama vase

Vezava spremenljivk ni enako prirejanju vrednosti spremenljivki! Spremenljivko je možno vezati večkrat. Nova vezava zasenči (angl. shadow) prejšnjo vezavo (slaba programerska praksa).

1.1.2.1.2 Program v SML?

Program je zaporedje vezav (angl. binding, spremenljivko povežemo z njeno vrednostjo), primer:

val x = 3       (* vezava spremenljivke x *)
val y = 5       (* podpičja lahko izpustimo *)
val z = x + y   (* matematična operacija *)
val uspesno = if z > 5 then true else false   (* pogojni stavek *)

1.1.2.1.3 Seštevanje

SINTAKSA

e1 + e2

e1 in e2 sta vgnezdena izraza (podizraza)

SEMANTIČNA PRAVILA

Pravilnost tipov

če je e1 tipa int in je e2 tipa int, je rezultat tipa int
Način evalvacije

če je vrednost izraza e1 enaka v1
in vrednost izraza e2 enaka v2,
je vrednost izraza e1+e2 enaka v1+v2

1.1.2.1.4 Pogojni stavki

SINTAKSA

if e1 then e2 else e3

e1, e2 in e3 so vgnezdeni izrazi

SEMANTIČNA PRAVILA

Pravilnost tipov

e1 mora biti tipa bool
e2 in e3 morata biti enakega tipa (!!!) - imenujmo ga t
rezultat celega izraza je tipa t
Način evalvacije

evalviraj e1 v vrednost v1
če je v1 enako true, evalviraj e2 v v2; v2 je rezultat
če je v1 enako false, evalviraj e3 v v3; v3 je rezultat

1.1.2.1.5 Programske napake

Kakšni so primeri tipičnih napak?

sintaktične napake
napake preverjanja tipov
napake pri evalvaciji

Poglejmo si primere…

(* PRIMERI SINTAKTIČNIH, TIPSKIH in EVALVACIJSKIH NAPAK *)

> val x = 34
val x = 34 : int

> val y = x + 1
val y = 35 : int

> val z = if y=1 then 34 else 4
val z = 4 : int

> val q = if y > 0 then 0 else 1
val q = 0 : int

> val a = ~5
val a = ~5 : int

> val w = 0
val w = 0

> val fun1 = 34
val fun1 = 34 : int

> val v = x * w
val v = 0 : int

> val fourteen = 7 - 7
val fourteen = 0 : int

(* prikaz senčenja *)

> val a = 3
> val b = 2*a
> val a = 5
val a = <hidden-value> : int
val b = 6 : int
val a = 5 : int

> val a = a + 1
val a = 6 : int

(* END prikaz senčenja *)

1.1.2.1.6 Funkcije

Kot jih že poznamo: imajo argumente in vračajo rezultat.

Deklaracija funkcije:

fun obseg(r: real) =
   2.0 * Math.pi * r

Funkcija se hrani kot vrednost, ki slika vhodni argument v izhodnega:

val obseg = fn : real -> real

Klic funkcije:

obseg(2.5);
obseg (2.5);
obseg 2.5;

1.1.2.1.6.1 Primeri funkcij

Pogojni stavek (vejanje) poznamo, kako pa doseči ponavljanje (zanko)?

konstrukta za zankanje programa (for, while, repeat) nimamo
odgovor: s klicem funkcije (same sebe - rekurzija)!

Napiši funkcije, ki izračunajo:

obseg krožnice pri podanem polmeru,
potenco xy (x in y sta podani naravni števili),
faktorielo podanega števila n,
vsoto naravnih števil od 1 do n,
vsoto naravnih števil od a do b.

fun obseg (r: real) = 
    2.0 * Math.pi * r

fun potenca (x: int, y: int) =
    if y=0
    then 1
    else x * potenca(x, y-1)

fun faktoriela (n: int) =
    if n=0
    then 1
    else n * faktoriela(n-1)

fun sestej1N (n: int) =
    if n=1
    then 1
    else sestej1N(n-1) + n

fun sestejAB (a: int, b: int) =    (* sestejemo vsa naravna stevila od a do b *)
    if a=b
    then a
    else sestejAB(a, b-1) + b

fun sestej1N_easy (n: int) =
    sestejAB (1, n)

1.1.2.1.6.2 Podrobno o funkcijah

Funkcije se obravnavajo kot vrednosti, ki se evalvirajo kasneje (ob klicu).
Znak * v zapisu tipov argumentov funkcije (int * int -> int) ne pomeni množenja ampak loči argumente funkcije.
Funkcije lahko kličejo samo funkcije, ki so že definirane v kontekstu (torej definirane prej ali same sebe).
Oznake tipov lahko pogosto izpustimo in pustimo, da SML sam sklepa na njih.

(* SML obvlada tudi sklepanje na podatkovne tipe iz stat. konteksta *)
    
fun obseg2 r = 
    2.0 * Math.pi * r

fun faktoriela2 n =
    if n=0
    then 1
    else n * faktoriela(n-1)

1.1.2.1.6.3 Formalno - Deklaracija funkcije

SINTAKSA

fun x0 (x1: t1, ... , xn: tn) = e

argument xi je tipa ti; telo funkcije je izraz e

SEMANTIČNA PRAVILA

Pravilnost tipov

uspešno, če ob klicu v statičnem okolju velja x1: t1, ..., xn: tn
in x0 : (t1 * ... * tn) -> t (za rekurzijo)
Način evalvacije

vezava doda x0 v okolje (da lahko funkcijo kličemo)

1.1.2.1.6.4 Formalno - Klic funkcije

SINTAKSA

e0 (e1, ... , en)

SEMANTIČNA PRAVILA

Pravilnost tipov

uspešno, če ima e0 tip (t1 * ... * tn) -> t
in velja e1: t1, ..., en: tn
tedaj: e0(e1,...,en) ima tip t
Način evalvacije

evalviraj e0 v fun x0 (x1 : t1, ... , xn : tn) = e
evalviraj argumente e1, ..., en v vrednosti v1, ..., vn
evalviraj telo e, pri čemer preslikaj x1 v v1, ..., xn v vn
telo e naj vsebuje x0

1.2 Podatkovni tipi, vezave, vzorci, polimorfizem, izjeme

Ponovimo

prednosti funkcijskega programiranja
vezave spremenljivk in funkcij
statično in dinamično okolje
enostavni izrazi (seštevanje, if-then-else)
sintaktična in semantična evalvacija konstruktov programskega jezika
podatkovni tipi:
- int
- bool
- real
- int * int -> int
uporaba rekurzije

Pregled

sestavljeni podatkovni tipi
- terke (angl. tuples)
- seznami (angl. lists)
- zapisi (angl. records)
vezave v lokalnem okolju
podatkovni tip „opcija“ (angl. option)
sinonimi za podatkovne tipe
izdelava lastnih podatkovnih tipov
ujemanje vzorcev s stavkom case
definicija seznama in opcije
polimorfizem podatkovnih tipov
ujemanje vzorcev pri deklaracijah
rekurzivno ujemanje vzorcev
sklepanje na podatkovni tip
izjeme

1.2.1 Sestavljeni podatkovni tipi

1.2.1.1 Terka (angl. tuple)

Podatkovni tip nespremenljive dolžine, sestavljen iz komponent različnih podatkovnih tipov.

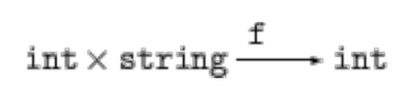
Zapis terke:

(e1, e2, ..., en)

če je podatkovni tip e1: t1, ..., en: tn,
je terka tipa t1 * t2 * ... * tn

Dostop do elementov terke e:

#n e

kjer je n številka zaporedne komponente, e pa izraz-terka

Primeri uporabe terk

Napiši funkcije, s katerimi:

seštej števili, predstavljeni s terko (parom)
```
fn : int * int -> int
```
obrni komponenti terke
```
fn : int * int -> int * int
```

prepleti dve trimestni terki

fn : (int * int * int) * (int * int * int)
-> int * int * int * int * int * int

sortiraj komponenti terk po velikosti
```
fn : int * int -> int * int
```

(* sestej stevili, podani v terki *)
fun vsota (stevili: int*int) =
    (#1 stevili) + (#2 stevili)

(* obrni elementa terke-para *)
fun obrni (stevili: int*int) =
    (#2 stevili, #1 stevili)

(* prepleti dve trimestni terki *)
fun prepleti (terka1: int*int*int, terka2: int*int*int) =
    (#1 terka1, #1 terka2, #2 terka1, #2 terka2, #3 terka1, #3 terka2)

(* sortiraj par stevil v terki po velikosti *)
fun sortiraj_par (terka: int*int) =
    if #1 terka < #2 terka
    then terka
    else (#2 terka, #1 terka)

1.2.1.2 Seznam (angl. list)

Podatkovni tip poljubne dolžine, sestavljen iz komponent enakih podatkovnih tipov.

flowchart LR
   1[1] --> 2[2] --> 5[5] --> 5_2[5] --> 3[3] --o END:::hidden

Zapis seznama s komponentami:

[v1, v2, ..., vn]

vsi elementi so istega podatkovnega tipa t

Zapis seznama s sintakso:

glava::rep

če je glava vrednost v0 in rep vrednost [v1, v2, ..., vn],
ima zapis glava::rep vrednost [v0, v1, ..., vn]
pozor: glava je element, rep je seznam!

Podatkovni tipi seznama:

int list, real list,(int * bool) list, int list list, ...

Dostop do elementov seznama:

null e

vrne true, če je seznam prazen – [ ]
```
fn : 'a list -> bool
```
hd e

vrne glavo seznama (element)
```
fn : 'a list -> 'a
```
tl e

vrne rep seznama (ki je seznam)
```
fn : 'a list -> 'a list
```

hd in tl prožita izjemo (exception), če je seznam prazen

Primeri seznamov

Naloge:

preštej število elementov v seznamu
```
fn : int list -> int
```
izračunaj vsoto elementov v seznamu
```
fn : int list -> int
```
vrni n-ti zaporedni element seznama
```
fn : int list * int -> int
```
združi dva seznama
```
fn : int list * int list -> int list
```
prepleti elemente obeh seznamov (do dolžine krajšega seznama)
```
fn : int list * int list -> (int * int) list
```
izračunaj vsote elementov v terkah (parih števil) v seznamu
```
fn : (int * int) list -> int list
```
filtriraj seznam predmetov glede na pozitivno oceno izpita
```
fn : (string * int) list -> string list
```

(* stevilo elementov v seznamu *)
fun stevilo_el(sez: int list) =
   if null sez
   then 0
   else 1 + stevilo_el(tl sez)

(* vsota elementov v seznamu *)
fun vsota_el(sez: int list) =
   if null sez
   then 0
   else hd sez + vsota_el(tl sez)

(* n-ti element seznama *)
fun n_ti_element(sez: int list, n: int) =
   if n=1
   then hd sez
   else n_ti_element(tl sez, n-1)

(* konkatenacija seznamov - append *)
fun zdruzi_sez(sez1: int list, sez2: int list) =
   if null sez1
   then sez2
   else (hd sez1)::zdruzi_sez(tl sez1, sez2)

(* prepletemo seznama v terke do dolzine krajsega od seznamov *)
fun prepleti_sez(sez1: int list, sez2: int list) =
   if null sez1 orelse null sez2
   then []
   else (hd sez1, hd sez2)::prepleti_sez(tl sez1, tl sez2)

(* vsota parov elementov v terkah vzdolz seznama *)
fun vsota_parov(sez: (int*int) list) =
   if null sez
   then []
   else (#1 (hd sez) + #2 (hd sez))::vsota_parov(tl sez)

(* filtiranje imen predmetov, kjer smo dobili pozitivno oceno *)
fun filter_poz_ocen(sez: (string*int) list) =
   if null sez
   then []
   else if #2 (hd sez) > 5 
         then (#1 (hd sez))::filter_poz_ocen(tl sez)
         else filter_poz_ocen(tl sez)

1.2.2 Lokalno okolje (vezave v lokalnem okolju)

Funkcije uporabljajo globalno statično/dinamično okolje ➔ potrebujemo konstrukt za izvedbo lokalnih vezav v funkciji:

lepše programiranje
potrebne so samo lokalno
zaščita pred spremembami izven lokalnega okolja
v določenih primerih: nujno za performanse (sledi…)!

Izraz „let“:

je samo izraz, torej je lahko vsebina funkcije
sintaksa:
```
let d1 d2 ... dn in e end
```
preverjanje tipov: preveri tip vezav d1, ..., dn in telesa e v zunanjem statičnem okolju. Tip celega izraza let je tip izraza e.
evalvacija: evalviraj zaporedoma vse vezave in telo e v zunanjem okolju. Rezultat izraza let je rezultat evalvacije telesa e.

Novost: uvedemo pojem dosega spremenljivke (angl. scope). V lokalnem okolju imamo lahko tudi vezave lokalnih funkcij.

fun sestej(c: int) =
   let
      val a = 5
      val b = a+c+1
   in
      a+b+c
   end

- val sestej = fn : int -> int

(* uporaba notranje pomozne funkcije *)
fun povprecje(sez: int list) =
   let
      fun stevilo_el(sez: int list) =
         if null sez
         then 0
         else 1 + stevilo_el(tl sez)
      fun vsota_el(sez: int list) =
         if null sez
         then 0
         else hd sez + vsota_el(tl sez)
      val vsota = Real.fromInt(vsota_el(sez))
      val n = Real.fromInt(stevilo_el(sez))
   in
      vsota/n
   end

- val povprecje = fn : int list -> real

Notranje funkcije lahko uporabljajo zunanje vezave, odvečne (podvojene) reference lahko torej odstranimo.

(* primer: odstranitev odvecnih parametrov *)
fun sestej1N (|arrow_start||n: int|color:cornflowerblue|) =    
                           |b je vedno enak n in se med rekurzijo ne spreminja!|color:cornflowerblue|
   let
      fun sestejAB (a: int, |arrow_end||b: int|color:red|) = (* pomozna funkcija *)
         if a=|b|color:red| then a else a + sestejAB(a+1,|b|color:red|)
   in
      sestejAB(1, |n|color:cornflowerblue|)
   end

Še lepše:

(* primer: odstranitev odvecnih parametrov *)
fun sestej1N (n: int) =
    let
        fun sestejAB (a: int) = (* odstranimo parameter b *)
            if a=n then a else a + sestejAB(a+1)
    in
        sestejAB(1)
    end

- val sestej1N = fn : int -> int

1.2.2.1 (Ne)učinkovitost rekurzije

Težave lahko nastopijo pri večkratnih rekurzivnih klicih.

fun najvecji_el (sez : int list) =
    if null sez
    then 0 (* maksimum praznega seznama je 0? *)
    else if null (tl sez)
         then hd sez
         else if hd sez > |najvecji_el(tl sez)|color:red|
               then hd sez
               else |najvecji_el(tl sez)|color:red|

(Brez težav) izvedba v primeru klica:

najvecji_el [30,29,28,27,26,...,7,6,5,4,3,2,1]

Vedno se kliče samo prvi rekurzivni klic (glava je večja od maksimuma v repu), torej:

najvecji_el[30,...,1] ➔ najvecji_el[29,...,1] ➔ najvecji_el[28,...,1] ➔ ... ➔ najvecji_el[1] ➔ konec

1.2.2.2 Učinkovitost rekurzije

fun najvecji_el (sez : int list) =
    if null sez
    then 0 (* maksimum praznega seznama je 0? *)
    else if null (tl sez)
         then hd sez
         else if hd sez > |najvecji_el(tl sez)|color:red|
               then hd sez
               else |najvecji_el(tl sez)|color:red|

Kaj pa izvedba v primeru klica:

najvecji_el [1,2,3,4,5,6,7,8,9,10,...,26,27,28,29,30]

Vedno se kličeta oba rekurzivna klica, torej:

najvecji_el [1,2,...,30]
➢  najvecji_el [2,...,30]
    ➢  najvecji_el [3,...,30]
        ➢  ...
        ➢  ...
    ➢  najvecji_el [3,...,30]
        ➢  ...
        ➢  ...
➢  najvecji_el [2,...,30]
    ➢  ...
        ➢  ...

Namesto 30 klicev jih imamo … koliko?

V primeru seznama dolžine n = 30 se zaradi dvojnega rekurzivnega klica (označenega z rdečo) funkcija obnaša eksponentno.

Za vsak element v seznamu se funkcija pokliče dvakrat, kar vodi do drevesa klicev, kjer se na vsakem nivoju število klicev podvoji. Torej:

Nivo 1: 1 klic
Nivo 2: 2 klica
Nivo 3: 4 klici
Nivo 4: 8 klicev
…itd.

Za seznam dolžine 30 to pomeni:

Število nivojev = 30 (globina rekurzije)
Na vsakem nivoju: $2^{(nivo-1)}$ klicev
Skupno število klicev = $2^0 + 2^1 + 2^2 + ... + 2^{29}$

To je geometrijska vrsta s količnikom 2, katere vsota je:

$2^{30} - 1 = 1,073,741,823$ klicev

Torej namesto linearnih 30 klicev imamo preko milijardo klicev! To je izjemno neučinkovito.

(TODO: verify)

Rešitev: uporaba lokalne spremenljivke, ki hrani rezultat rekurzivnega klica.

fun najvecji_el (sez : int list) =
    if null sez
    then 0
    else if null (tl sez)
         then hd sez
         else |let val max_rep = najvecji_el (tl sez)|bg:pink|
              |   in                                 |bg:pink|
              |       if hd sez > max_rep            |bg:pink|
              |       then hd sez                    |bg:pink|
              |       else max_rep                   |bg:pink|
              |   end                                |bg:pink|

Problem

V premislek:

Kateri je minimalni element praznega seznama?
Katero je zaporedno mesto (pozicija v seznamu) podanega elementa, ki ga v seznamu ni?

Kaj vrniti kot odgovor?

-1?
[ ]?
null?
prožiti izjemo?

Rešitev v SML: opcija, vezana na podatkovni tip:

SOME <rezultat>, če rezultat obstaja
NONE, če rezultat ni veljaven

1.2.3 Opcije (podatkovni tip „opcija“ (angl. option))

Tip t option (npr. int option, string option, …)

podobno kot “list” v primerih: int list, (int*bool) list itd.

Zapis opcije

SOME e ➔ če je e tipa t, je SOME e tipa t option
NONE ➔ je tipa 'a option

Dostop do opcije

isSome: preveri, ali je opcija v obliki SOME
```
val it = fn : 'a option -> bool
```
valOf: vrne vrednost e opcije SOME e
```
val it = fn : 'a option -> 'a
```

Izboljšava iskanja elementa

Primer: iskanje prve lokacije podanega elementa

(* poiscemo prvo lokacijo pojavitve elementa el *)
(* (int list * int) -> int option *)

fun najdi(sez: int list, el: int) =
   if null sez
   then |NONE|color:green|
   else if (hd sez = el)
         then |SOME 1|color:green|
         else let val preostanek = najdi (tl sez, el)
            in if |isSome|color:green| preostanek
               then |SOME (1 + valOf preostanek)|color:green|
               else |NONE|color:green|
            end

- val najdi = fn : int list * int -> int option

Podatkovni tipi – do sedaj

enostavni PT
- int
- bool
- real
- string
- char

sestavljeni (kompleksni) podatkovni tipi
- terke (e1, e2, ..., en) – tip t1 * t2 * ... *tn
- seznami [e1, e2, ..., en] – tip 'a list
- opcije SOME e, NONE – tip 'a option
- zapisi: NASLEDNJA TEMA

izdelava lastnih podatkovnih tipov?: NASLEDNJA TEMA

1.2.4 Zapis (angl. record)

Podatkovni tip s poljubnim številom imenovanih polj, ki hranijo vrednosti (lahko različnih podatkovnih podtipov).

JS primer:

{
   name: "sue", // |<--- field: value|color:cornflowerblue|
   age: 26,     // |<--- field: value|color:cornflowerblue|
   status: "A"  // |<--- field: value|color:cornflowerblue|
}

Zapis zapisa:

{polje1 = e1, polje2 = e2, ..., poljen = en}

če je podatkovni tip komponent enak e1: t1, ..., en: tn, ima celotni zapis podatkovni tip {polje1: t1, ..., poljen: tn}
- vrstni red polj ni pomemben (SML prikaže v abecednem vrstnem redu)
- tipi so lahko enostavni ali sestavljeni
- podani so lahko izrazi, ki se pri deklaraciji evalvirajo v vrednosti
- SML implicitno deklarira novi tip zapisa (ni treba tega narediti nam)

Dostop do elementov zapisa e:

#ime_polja e

Primer uporabe zapisa

> val zapis = {ime="Dejan", starost=21, absolvent=false, 
    ocene=[("angl",8),("ars",10)] }
val zapis =
  {absolvent=false,ime="Dejan",ocene=[("angl",8),("ars",10)],starost=21}
  : {absolvent:bool, ime:string, ocene:(string * int) list, starost:int}
    
> #absolvent zapis;
val it = false : bool

> #ocene zapis;
val it = [("angl",8),("ars",10)] : (string * int) list

> (#ime zapis) ^ " je star " ^ Int.toString(#starost zapis) ^ " let."
val it = "Dejan je star 21 let." : string

S predavanj:

> fun izpis_studenta (zapis: {absolvent:bool, ime:string, ocene:(string * int) list, starost:int}) =
   (#ime zapis) ^ " je star " ^  Int.toString(#starost zapis) ^ " let."
val izpis_studenta = fn
  : {absolvent:bool, ime:string, ocene:(string * int) list, starost:int}
    -> string

1.2.4.1 Sinonimi za podatkovne tipe

Pogosto uporabljene in kompleksne (dolge) nazive podatkovnih tipov lahko poimenujemo z lastnim imenom in si poenostavimo delo.

type novo_ime = tip

fun izpis_studenta (zapis: {absolvent:bool, ime:string, 
    ocene:(string * int) list, starost:int}) =
    
    (#ime zapis) ^ " je star " ^ Int.toString(#starost zapis) ^ " let."

⬇

type student = {absolvent:bool, ime:string,
    ocene:(string * int) list, starost:int}

fun izpis_studenta2 (zapis: student) =
    (#ime zapis) ^ " je star " ^ Int.toString(#starost zapis) ^ " let."

Obe imeni tipov sta ekvivalentni. SML lahko pri zapisovanju funkcij uporablja novo ali staro (dolgo) ime tipa (nepomembno).

val izpis_studenta2 = fn : student -> string

Dodaten primer:

(* primer 2: artikli v trgovini *)
type artikel = string * int

fun najmanj2mleka (a: artikel) =
   (#1 a = "mleko") andalso (#2 a >=2)   

fun prestejizdelke(sa: artikel list): int =
   if null sa
   then 0
   else #2 (hd sa) + prestejizdelke(tl sa)

1.2.4.2 Terke in zapisi

Poglejmo si zanimiv primer…

                                    |arrow_start||deklaracija novega zapisa|color:cornflowerblue|

val test = {1="Zivjo", 2="adijo"|arrow_end|}; (* enakovredno terki *)

- val test = ("Zivjo","adijo") : string *|arrow_start| string

                                          |arrow_end||rezultat je podatkovni tip terke?|color:red|

Poseben tip “terka” torej v programskem jeziku ne obstaja! Terka je torej samo sintaktična olepšava/bližnjica za posebno obliko zapisa:

zapis (e1,...,en) namesto {1=e1,...,n=en}
zapis podatkovnega tipa t1*...*tn namesto {1:t1, ..., n:tn}

Terka – naslavljanje po vrstnem redu argumentov; zapis – naslavljanje po imenih argumentov

Kdaj pri programiranju uporabljamo enega in drugega?

Kdaj uporabiti terke:

Ko imamo manjše število povezanih vrednosti (običajno 2-3)
Ko je vrstni red elementov naraven ali očiten (npr. koordinate x,y)
Ko je struktura podatkov začasna ali lokalna
V primerih kjer je sintaksa bolj berljiva s terko

Kdaj uporabiti zapise:

Ko imamo več povezanih vrednosti
Ko želimo jasno dokumentirati pomen posameznih polj
Ko vrstni red polj ni intuitiven
Za kompleksnejše podatkovne strukture
Ko se struktura uporablja širše v programu

// TODO: verify

Terke ali polja?

pri majhnem številu elementov nam ni potrebno pomniti imen polj,
pri velikem številu elementov lažje pomnimo komponente po imenu kot po vrstnem redu

1.2.5 Izdelava lastnih podatkovnih tipov

Deklaracija novega podatkovnega tipa, ki predstavlja alternativo med podatkovnimi tipi, iz katerih je sestavljen:

datatype prevozno_sredstvo = |Bus|color:cornflowerblue| of int
                           | |Avto|color:cornflowerblue| of string * string
                           | |arrow_end||Pes|color:cornflowerblue|     |<-------------> <-vsebina podatkovnega tipa|color:cornflowerblue|

                           |arrow_start||konstruktorji|color:cornflowerblue|

- datatype prevozno_sredstvo = Avto of string * string | Bus of int | Pes

Ali obstaja kaj podobnega v drugih programskih jezikih?

V drugih programskih jezikih obstajajo podobni koncepti za definiranje lastnih podatkovnih tipov.

Npr.: Rust - Enums (najbolj podobno ML):

enum PrevoznoSredstvo {
   Bus(i32),
   Avto(String, String),
   Pes
}

Imajo pa tudi ostali jeziki (Kotlin, Java, Python, itd.).

Rezultat:

v okolju definiramo novi podatkovni tip prevozno_sredstvo
v okolju definiramo konstruktorje za izdelavo novih podatkovnih tipov: Bus, Avto in Pes

1.2.5.1 Vrednosti lastnih podatkovnih tipov

Vrednost novega podatkovnega tipa je vedno sestavljena z oznako konstruktorja (+ vrednost), npr:

Bus 1
Avto ("fiat", "modri")
Pes

Konstruktorja Bus in Avto sta funkciji, ki vrneta vrednost novega podatkovnega tipa:

fn : int -> prevozno_sredstvo
fn : string * string -> prevozno_sredstvo

Konstruktor Pes ne potrebuje argumenta in že sam predstavlja vrednost:

val it = Pes : prevozno_sredstvo

Vrednost novega pod. tipa lahko opredelimo tudi z izrazom, npr. Bus (1+5)

1.2.5.2 Prednosti?

Omogoča definiranje različnih alternativ za zapis podatka:

Namesto redundantnih zapisov:

(* ce nacin =1 glej polje bus;
   ce = 2, glej avto; ce je 3 glej pes *)
{ nacin: int, 
   bus: int,
   avto: string*string,
   pes: boolean}

Ustvarimo eleganten (izključujoč) podatkovni tip:

datatype prevozno_sredstvo = Bus of int
                           | Avto of string * string
                           | Pes

Omogoča rekurzivno definiranje tipa (pomembno za sezname, kasneje podrobno o tem…)

1.2.5.3 Delo z lastnimi podatkovnimi tipi

Lastni podatkovni tipi predstavljajo alternativne komponente.

(Teoretično) imamo dve možnosti načina uporabe:

Pri programiranju sproti preverjati, s katerim podtipom dejansko delamo (ali je tip prevozno_sredstvo dejansko vrste Bus, Avto ali Pes?)
- uporaba funkcij, kot bi bile isBus, isAvto (podobno kot isSome in null), in pridobiti podatke npr. z getBusInt, getAvtoStrStr
  (podobno kot hd, tl, valOf)
- tak način je pogosto prisoten v dinamično tipiziranih jezikih (kako je s tem pri Javi?)
Podatek primerjati z različnimi vzorci:
- SML uporablja sistem primerjanja z vzorci!
- stavek case ⬅ ☺

1.2.6 Stavek case

primerja podani izraz e0 za ujemanje z vzorci p1, ..., pn
rezultat je (samo eden) izraz na desni strani vzorca, s katerim se e0 ujema
vse veje e1, ..., en morajo biti istega podatkovnega tipa

case e0 of
    |p1|color:cornflowerblue| => e1
  || p2|color:cornflowerblue| => e2
    ...
  ||arrow_end|| pn|color:cornflowerblue| => en

    |arrow_start||vzorci|color:cornflowerblue|

Primer:

naši vzorci so možne alternative podatkovnega tipa (konstruktor + spremenljivka)
spremenljivke v vzorcu dobijo dejanske vrednosti glede na podani argument

fun obdelaj_prevoz x =
    case x of
        Bus i => i+10
        | Avto (s1,s2) => String.size s1 + String.size s2
        | Pes => 0

Prednosti ujemanja vzorcev (in stavka case)?

okolje nas opozori, če pozabimo na primer vzorca
okolje nas opozori, če podvojimo vzorec
izognemo se okoliščinam, ko na podatkovnem tipu uporabimo napačno metodo za pridobitev vrednosti (npr. valOf na vrednosti NONE ali hd na seznamu [])
lažje delo s funkcijami ➔ sledi v nadaljevanju

Kdaj vendarle uporabiti funkcije za preverjanje PT in ekstrakcijo podatkov (null, hd, tl)?

v argumentih funkcijskih klicev
kadar je preglednost programa večja

Primer: aritmetični izrazi

Definirajmo izraz kot rekurzivni (!) podatkovni tip:

datatype izraz = Konstanta of int
                | Negiraj of izraz
                | Plus of izraz * izraz
                | Minus of izraz * izraz
                | Krat of izraz * izraz
                | Deljeno of izraz * izraz
                | Ostanek of izraz * izraz

Primer izraza:

Plus (Konstanta 3, Ostanek(Konstanta 18, Konstanta 4)

Izraze lahko predstavimo z drevesno strukturo:

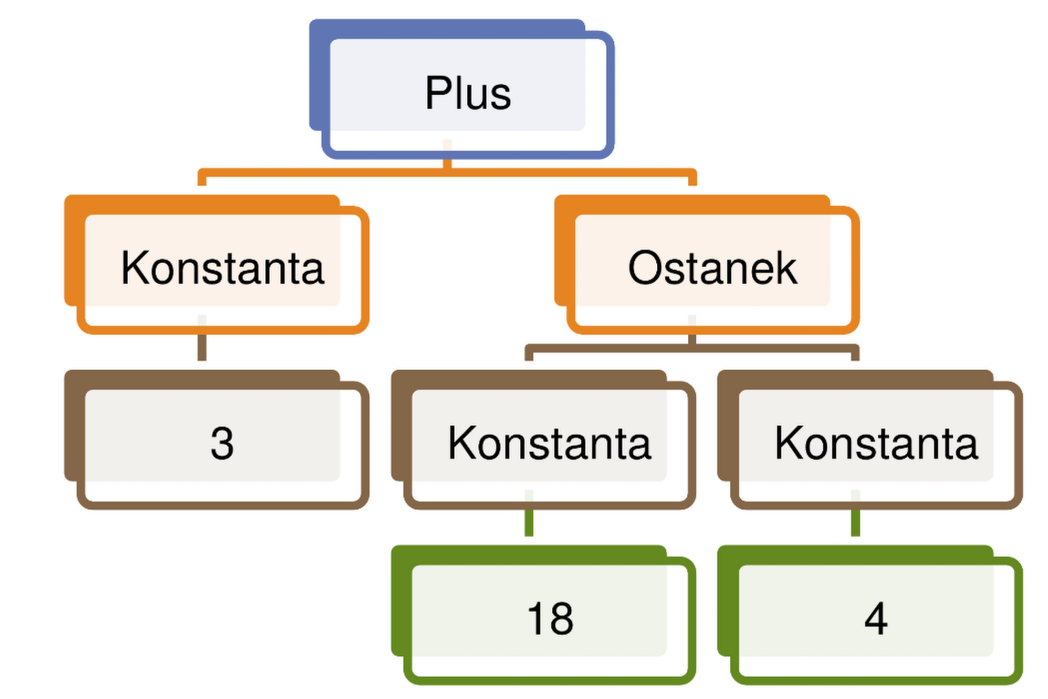
Naloge: aritmetični izrazi

Napiši funkcije tipa fn : izraz -> int, s katerimi:

evalviraj vrednost aritmetičnega izraza
preštej število negacij v izrazu
poišči maksimalno konstanto v izrazu (domača naloga za vajo)
poišči število primerov, kjer je ostanek pri deljenju enak 0 (domača naloga za vajo)

datatype izraz =  Konstanta of int 
      | Negiraj of izraz
      | Plus of izraz * izraz
      | Minus of izraz * izraz
      | Krat of izraz * izraz
      | Deljeno of izraz * izraz
      | Ostanek of izraz * izraz

val izraz1 = Konstanta 3
val izraz2 = Negiraj (Konstanta 3)
val izraz3 = Plus (Konstanta 3, Ostanek(Konstanta 18, Konstanta 4))
val izraz4 = Deljeno (izraz3, Negiraj izraz2)

fun eval e =
   case e of
      Konstanta i => i
      | Negiraj e  => ~ (eval e)
      | Plus(e1,e2) => (eval e1) + (eval e2)
      | Minus(e1,e2) => (eval e1) - (eval e2)
      | Krat(e1,e2) => (eval e1) * (eval e2)
      | Deljeno(e1,e2) => (eval e1) div (eval e2)
      | Ostanek(e1,e2) => (eval e1) mod (eval e2)

fun stevilo_negacij e =
   case e of
      Konstanta i => 0
      | Negiraj e  => (stevilo_negacij e) + 1
      | Minus(e1,e2) => (stevilo_negacij e1) + (stevilo_negacij e2)
      | Krat(e1,e2) => (stevilo_negacij e1) + (stevilo_negacij e2)
      | Deljeno(e1,e2) => (stevilo_negacij e1) + (stevilo_negacij e2)
      | Ostanek(e1,e2) => (stevilo_negacij e1) + (stevilo_negacij e2)

// TODO:

1.2.7 Definicija seznama in opcije

1.2.7.1 Resnica o seznamih in opcijah

Le sintaktična olepšava v programskem jeziku (niso nujno potrebna komponenta).
Definirana sta kot rekurzivna podatkovna tipa.

Iz dokumentacije SML:

SEZNAM

               |arrow_start||dodatni parameter za polimorfizem tipa|color:cornflowerblue|

datatype 'a|arrow_end| list = nil
                  | :: of 'a * 'a list

OPCIJA

datatype 'a option = NONE
                    | SOME of 'a

1.2.7.2 Seznami kot rekurzivni podatkovni tip

datatype 'a list = nil
                  | :: of 'a * 'a list

'a list = potrebno za polimorfizem (več o tem kasneje)

nil = prazen seznam (enakovredno zapisu [ ] )

:: = konstruktor

'a * 'a list =

'a = glava
'a list = rep

Posebnost: konstruktor :: je definiran kot infiksni operator (izjema), zato ne moremo zapisati ::(glava, rep), temveč pišemo glava::rep:

> 3::5::1::nil;
val it = [3,5,1] : int list

Ker seznami uporabljajo konstruktorje, lahko tudi na njih izvajamo ujemanje vzorcev (namesto uporabe hd, tl, null). Funkcije hd, tl in null znamo sedaj sprogramirati sami!

1.2.7.3 Opcija kot rekurzivni podatkovni tip

datatype 'a option = NONE
                    | SOME of 'a

'a option = potrebno za polimorfizem (več o tem kasneje)

NONE = konstruktor za “ni podatka”

SOME = konstruktor za podan podatek tipa 'a

'a = vrednost

Tudi pri opcijah lahko sedaj uporabimo ujemanje vzorcev. Funkcije valOf in isSome znamo sedaj sprogramirati sami!

S predavanj:

(* definicija lastnega seznama *)
datatype mojlist = konec
                  | Sez of int * mojlist

(* definicija lastne opcije *)
datatype intopcija = SOME of int
                     | NONE


(* SEZNAM - ujemanje vzorcev *)
fun glava sez =
   case sez of
      [] => 0 (* !!! kasneje: exception *)
      | prvi::ostali => prvi

fun prestej_elemente sez =
   case sez of
      [] => 0
      | glava::rep => 1 + prestej_elemente rep


(* OPCIJE - ujemanje vzorcev *)
fun vecji_od_5 opcija =
   case opcija of
      NONE => false
      | SOME x => (x>5)

1.2.8 Polimorfizem podatkovnih tipov

Novi podatkovni tip lahko uporablja poljuben drugi (vgnezdeni) podatkovni tip. Zahtevamo konsistentno rabo vgnezdenega tipa (pri vseh pojavitvah predstavlja 'a isti tip; enako velja za 'b, 'c itd.)

datatype |'a list|bg:orange| = nil
                  | :: of 'a * 'a list

datatype |'a option|bg:orange| = NONE
                     | SOME of 'a

Primer: izdelajmo lasten polimorfen podatkovni tip: seznam, ki hrani dva različna tipa podatkov:

datatype ('a, 'b) seznam =
        Elementa of ('a * ('a, 'b) seznam)
        | Elementb of ('b * ('a, 'b) seznam)
        | konec

Podatkovni tip ('a, 'b) seznam v Standard ML (SML) je rekurzivni tip, ki predstavlja seznam z elementi dveh različnih tipov ('a in 'b). Vsak element je označen s konstruktorjem Elementa (za tip 'a) ali Elementb (za tip 'b), konca seznama pa označuje konstruktor konec.

Struktura tipa:

Elementa of ('a * ('a, 'b) seznam):
- Predstavlja vozlišče s podatkom tipa 'a in repom, ki je nadaljevanje seznama.
- Primer: Elementa(5, ...) shrani celo število 5 in kaže na preostanek seznama.
Elementb of ('b * ('a, 'b) seznam):
- Predstavlja vozlišče s podatkom tipa 'b in repom, ki je nadaljevanje seznama.
- Primer: Elementb("abc", ...) shrani niz "abc".
konec
- Prazni seznam, ki označuje konec.

Značilnosti:

Heterogenost: Seznam lahko vsebuje elemente dveh različnih tipov ('a in 'b), ki se lahko poljubno izmenjujejo.
Rekurzivna definicija: Rep seznama je vedno tipa ('a, 'b) seznam.
Tipovna varnost: SML zagotovi, da so vsi elementi označeni s pravim konstruktorjem (npr. Elementa ne more vsebovati 'b).

Primer seznama:

val primer = Elementa(1, Elementb("dva", Elementa(3, konec)))

Tip: (int, string) seznam.
Struktura: 1 -> "dva" -> 3 -> konec.

Funkcije za delo s seznamom:

Primer funkcije, ki prešteje vse elemente:

fun dolzina konec = 0
  | dolzina (Elementa(_, xs)) = 1 + dolzina xs
  | dolzina (Elementb(_, xs)) = 1 + dolzina xs

Rezultat za primer je 3.

Primer funkcije, ki sešteje vse Elementa (če je 'a = int):

fun vsota_a konec = 0
  | vsota_a (Elementa(x, xs)) = x + vsota_a xs
  | vsota_a (Elementb(_, xs)) = vsota_a xs

Rezultat za primer je 4 (1 + 3).

Uporaba:

Takšen tip je uporaben za mešane sezname (npr. kombinacije števil in nizov), kjer je pomembno ločevati med tipi. Primeri:
- Zaporedje operacij (npr. število + nizovni ukaz).
- Razširljivi vnosni podatki (npr. številke in besedila).

(* s predavanj *)

(* fn: seznam -> (int * int) *)
fun prestej sez =
   case sez of
      Elementa(x, preostanek) => let val vp = prestej(preostanek)
                                 in (1 + (#1 vp), #2 vp)
                                 end
      | Elementb(x, preostanek) => let val vp = prestej(preostanek)
                                 in (#1 vp, 1 + (#2 vp))
                                 end
      | konec => (0,0)

1.2.9 Resnica o deklaracijah (ujemanje vzorcev pri deklaracijah)

Deklaracije spremenljivk in funkcij dejansko uporabljajo ujemanje vzorcev na mestu, kjer smo navajali ime spremenljivke:

val vzorec = e
fun ime vzorec = e

Zgornje pomeni, da vsaka funkcija sprejema natanko en argument, ki ga primerja z vzorcem ekvivalentna zapisa:

fun sestej1 (trojcek: int*int*int) =
    let val (a,b,c) = trojcek
    in a+b+c
    end

fun sestej2 (a,b,c) =   (* vzorec *)
    a + b + c

Dodatni primeri s predavanj:

> val (a,b,c) = (1,2,3);
val a = 1 : int
val b = 2 : int
val c = 3 : int

> val (a,b) = (3,(true,3.14));
val a = 3 : int
val b = (true,3.14) : bool * real

> val (a,(b,c)) = (3,(true,3.14));
val a = 3 : int
val b = true : bool
val c = 3.14 : real

> val {prva=a, tretja=c, druga=b} = {prva=true, druga=false, tretja=3};
val b = false : bool
val a = true : bool
val c = 3 : int

> val glava::rep = [1,2,3,4];
stdIn:5.5-5.27 Warning: binding not exhaustive
          glava :: rep = ...
val glava = 1 : int
val rep = [2,3,4] : int list

> val prvi::drugi::ostali = [1,2,3,4,5];
stdIn:6.5-6.38 Warning: binding not exhaustive
          prvi :: drugi :: ostali = ...
val prvi = 1 : int
val drugi = 2 : int
val ostali = [3,4,5] : int list

Je kakšna razlika med zapisom z vzorcem in zapisom “funkcije s tremi argumenti”?

Ključno spoznanje: Med zapisoma NI NOBENE semantične razlike!

Razlogi:

V SML vse funkcije sprejmejo natančno EN argument
Prvi zapis je samo sintaktični sladkorček (syntactic sugar) za drugi zapis
Ko napišemo f (x,y,z), je (x,y,z) v resnici vzorec, ki se ujema s trojčkom
SML prevajalnik oba zapisa obravnava popolnoma enako

(* s predavanj *)
fun povecaj (a,b,c) = (a+1,b+1,c+1) (* funkcije sprejemajo samo 1 argument *)

Kaj smo se danes naučili?

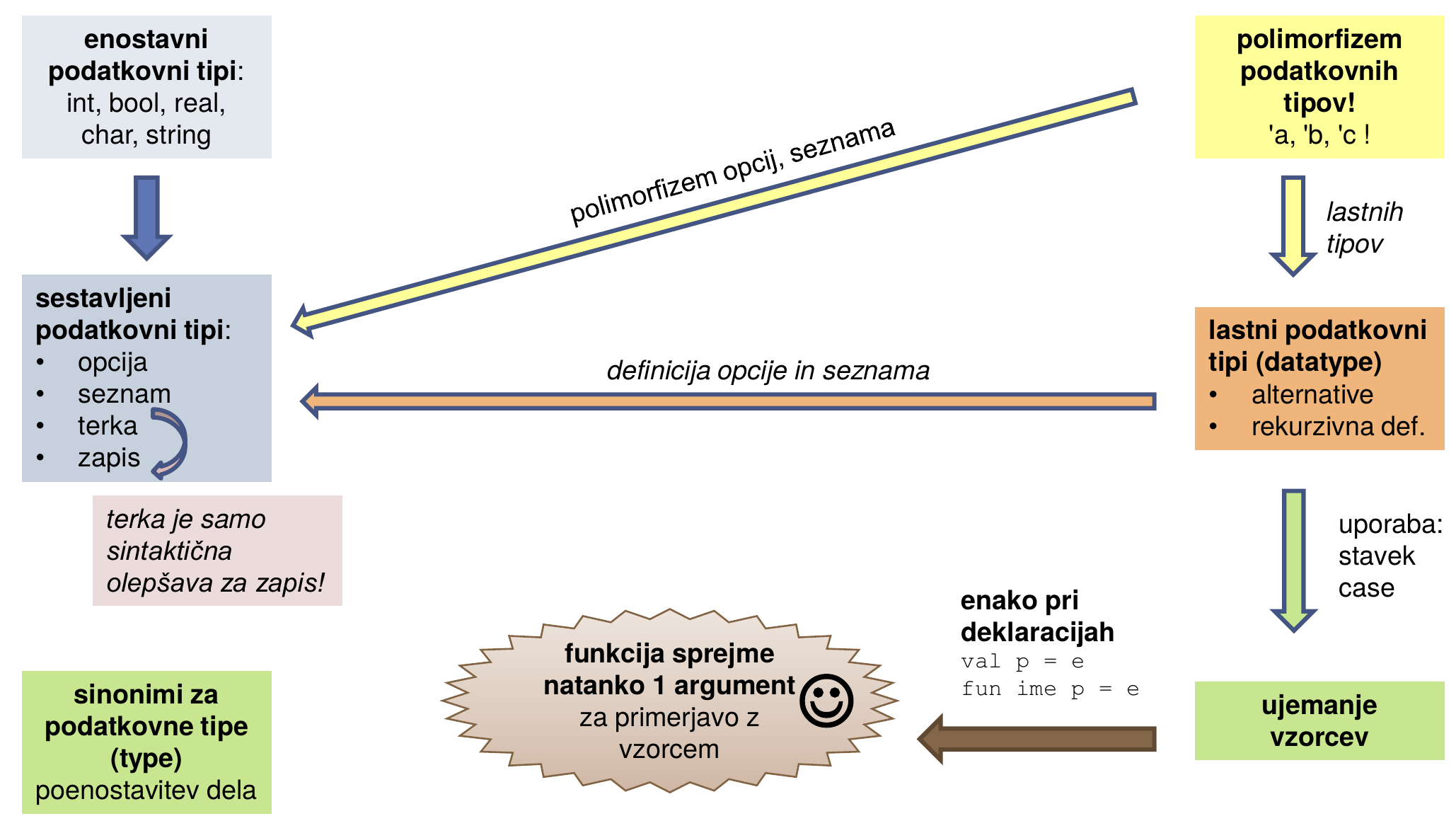
1.2.10 Rekurzivno ujemanje vzorcev

Namesto vgnezdenih stavkov case lahko vgnezdimo vzorce v vzorce (pri gnezdenju se tudi spremenljivke prilagodijo pravim vrednostim):

(glava1::rep1, glava2::rep2)
(glava::(drugi::(tretji::rep)))
((a1,b1)::rep)
...

Pri zapisovanju vzorcev lahko uporabimo anonimno spremenljivko _, ki se prilagodi delu izraza, ne veže pa rezultata na ime spremenljivke:

fun dolzina (sez:int list) =
    case sez of
        [] => 0
        | _|arrow_end|::rep => 1 + dolzina rep (* "_" NAMESTO: glava::rep *)

            |arrow_start|(* anonimna spremenljivka (pri računanju dolžine seznama
                  vrednosti elementov niso pomembne) *)

Primeri gnezdenja

Napiši naslednje programe:

Podana sta seznama sez1 in sez2. Seštej njune istoležne komponente v novi seznam. Da program uspe, morata biti oba seznama enako dolga.
```
fn : int list * int list -> int list
```
Podan je seznam, ki predstavlja zaporedje, izračunano po Fibonaccijevem zakonu. Preveri, ali je seznam veljavno takšno zaporedje.
```
fn : int list -> bool
```
Napiši program, ki za dve celi števili pove, ali je rezultat po njunem seštevanju sodo število, liho število ali ničla.
```
fn : int * int -> sodost
```

(***************************************************************)
(* 1. PRIMER *)
(* seštevanje dveh seznamov po elementih; seznama morata biti enako dolga *)

(* SLAB NACIN: *)
exception LengthProblem

fun sestej_seznama (sez1, sez2) =
   case sez1 of
      [] => (case sez2 of
               [] => []
               | glava::rep => raise LengthProblem)
      | glava1::rep1 => (case sez2 of
                           [] => raise LengthProblem
                           | glava2::rep2 => (glava1+glava2)::sestej_seznama(rep1,rep2))

(* BOLJSI NACIN z gnezdenjem vzorcev*)
fun sestej_seznama2 seznama =
   case seznama of
      ([], []) => []
      | (glava1::rep1, glava2::rep2) => (glava1+glava2)::sestej_seznama(rep1,rep2)
      | _ => raise LengthProblem


(***************************************************************)
(* 2. PRIMER *)
fun check_fibonacci sez =
    case sez of
      (glava::(drugi::(tretji::rep))) => (tretji = (glava+drugi)) andalso check_fibonacci (drugi::(tretji::rep))
      | _ => true


(***************************************************************)
(* 3. PRIMER *)
datatype sodost = S | L | N
- datatype sodost = L | N | S

fun sodost_sestevanje (a,b) = 
   let 
      fun sodost x = if x=0 then N
                     else if x mod 2 = 0 then S 
                     else L
   in
      case (sodost a, sodost b) of
         (S,L) => L
         | (S,_) => S
         | (L,L) => S
         | (L,_) => L
         | (N,x) => x
   end
- val sodost_sestevanje = fn : int * int -> sodost

1.2.11 Sklepanje na podatkovni tip

SML ima vgrajen sistem za sklepanje na podatkovni tip funkcije, tudi če ročno ne navajamo vhodnega in izhodnega tipa.

Pogoj za delovanje sistema:

uporabljati moramo ujemanje vzorcev, s katerim opredelimo vse spremenljivke, ki nastopajo v programski kodi
povedano drugače: v programu ne smemo naslavljati komponent spremenljivke z #zap_št ali #ime_polja (v primeru uporabe #… je potrebno eksplicitno navajanje tipov)

Zakaj?

SML zahteva eksplicitno navajanje tipov pri uporabi konstrukcij, kot so #zap_št ali #ime_polja, ker te konstrukcije ne zagotavljajo dovolj informacij za samodejno sklepanje tipov.

Ujemanje vzorcev pa omogoča, da sistem za sklepanje tipov deluje brez težav, saj jasno opredeli strukturo podatkov in vse njene komponente.

- fun sestej stevili = #1 stevili + #2 stevili;
|stdIn:4.1-5.28 Error: unresolved flex record|color:red|
   |(need to know the names of ALL the fields in this context)|color:red|

(* moramo opredeliti podatkovni tip *)
- fun sestej2 (stevili:int*int) =
-   #1 stevili + #2 stevili

(* sklepanje na tip deluje pri uporabi vzorcev *)
- fun sestej3 (s1, s2) =
-   s1 + s2
val sestej = fn : int * int -> int

1.2.11.1 Polimorfizem pri sklepanju na tip

Lahko se zgodi, da SML ugotovi, da so napisane funkcije bolj splošne, kot smo želeli. Tip je bolj splošen kot drugi tip, če lahko v njemu konsistentno zamenjamo bolj splošne tipe ('a, 'b, 'c) z manj splošnimi tipi (npr. vse 'a za int, vse 'b za string itd.)

(* ni polimorfna *)
fun vsota_el sez =
   case sez of
      [] => 0
      | glava::rep => glava + vsota_el rep

(* je polimorfna *)
fun zdruzi (sez1, sez2) =
    case sez1 of
        [] => sez2
        | glava::rep => glava::zdruzi(rep, sez2)

- val zdruzi = fn : |'a list|bg:orange| * |'a list|bg:orange| -> |'a list|bg:orange|

(* je polimorfna *)
fun sestej_zapis {prvi=a, drugi=b, tretji=c, cetrti=d, peti=e}
    = a+d

- val sestej_zapis = fn : {cetrti:int, drugi:|'a|bg:orange|, peti:|'b|bg:orange|, prvi:int, tretji:|'c|bg:orange|} -> int

Primeri specifičnih tipov

Kateri od naslednjih tipov so bolj specifični od tipa?

'a list * ('b * 'a) list -> 'a

   string list * ((int*int) * string) list -> string

```
   int list * (int * int) list -> int
```

   (int*bool) list * (bool * (int*bool)) list -> (int*bool)

   int list list * (bool * int list ) list -> int list

   int option list * (bool * int list) option -> int list

```
   real list * string list -> real
```

Bolj specifični tipi kot 'a list * ('b * 'a) list -> 'a so:

✅ Veljaven
string nadomesti 'a, (int*int) nadomesti 'b
Struktura se ujema: list * list s tuple elementi v drugem seznamu.
✅ Veljaven
int nadomesti tako 'a kot 'b
Struktura ohranjena: int list * (int * int) list.
✅ Veljaven
(int*bool) nadomesti 'a, bool nadomesti 'b
Struktura se ujema: (int*bool) list * (bool * (int*bool)) list.
✅ Veljaven
int list nadomesti 'a, bool nadomesti 'b
Struktura ohranjena: int list list * (bool * int list) list.
❌ Neveljaven
Drugi argument je option namesto list (list bi moral biti ker je malo naprej 'a definiran kot int list) Neujemajoč konstruktor tipa ((bool * int list) option namesto zahtevane strukture seznama).
❌ Neveljaven
Drugi argument je string list (elementi niso tuple)
Krši zahtevano strukturo ('b * 'a) tuple v originalnem tipu.

Odgovor: Možnosti 1, 2, 3 in 4 so bolj specifične.

1.2.11.2 Primerjalni podatkovni tipi

Naslednja funkcija:

fun f1 (a,b,c,d) =
    if a=b
    then c
    else d

Je polimorfnega tipa:

val f1 = fn : |arrow_end||''a|color:cornflowerblue| * |''a|color:cornflowerblue| * 'b * 'b -> 'b

                  |arrow_start||dva apostrofa označujeta primerjalni podatkovni tip|color:cornflowerblue|

Primerjalni podatkovni tip (angl. eqtype):

Je tudi polimorfni podatkovni tip.
Zanj mora veljati sposobnost primerjanja enakosti z drugim tipom (posledica “if a=b”) v funkciji.
Ker 'a pomeni “poljuben tip”, ''a pa “poljuben primerjalni tip”, je 'a bolj splošna oznaka kot ''a.
Zapis tipa (''a) torej predstavlja dodatno omejitev, na katero opozarja programerja.

1.2.12 Izjeme

Sporočajo o neveljavnih situacijah, do katerih je prišlo med izvajanjem programa.

Definicija/vezava izjeme:

exception MojaIzjema
exception MojaIzjema of int

Proženje izjeme:

raise MojaIzjema
raise MojaIzjema(7)

Obravnava izjeme:

e1 handle MojaIzjema => e2
e1 handle MojaIzjema(x) => e2

Izjeme so podatkovnega tipa exn.

Uporabimo jih lahko tudi v argumentih funkcij:

izjema v argumentu še ne proži izjeme, temveč jo samo opredeli
primer tipa funkcije:
```
fn : int * exn -> int list
```

Stavek handle se uporablja za obravnavo izjem; uporablja lahko ujemanje vzorcev (kot stavek case) in ima lahko več različnih vej:

fun deli (a1, a2, napaka) =
    if a2 = 0
    then raise napaka
    else a1 div a2

fun naredinekaj (stevilo, moja_napaka) =
    deli(stevilo, 0, moja_napaka)
    handle moja_napaka => ~9999999

Primeri s predavanj:

(* prej - brez uporabe izjem *)
fun glava sez =
   case sez of
      [] => 0 (* !!! kasneje: exception *)
      | prvi::ostali => prvi


(* z uporabo izjem *)
exception PrazenSeznam

- exception PrazenSeznam

fun glava sez =
   case sez of
      [] => raise PrazenSeznam
      | prvi::ostali => prvi

- val glava = fn : 'a list -> 'a

(***************************************************************)
(* primer izjeme pri deljenju z 0 *)
exception DeljenjeZNic

fun deli1 (a1, a2) =
   if a2 = 0 
   then raise DeljenjeZNic
   else a1 div a2

fun tabeliraj1 zacetna =
   deli1(zacetna,zacetna-5)::tabeliraj1(zacetna-1)
   handle DeljenjeZNic => [999]


(***************************************************************)
(* še bolj splošno: prenos izjeme v parametru *)
(* fn : int * int * exn -> int *)
fun deli2 (a1, a2, napaka) =
   if a2 = 0 
   then raise (* SPREMEMBA *) napaka
   else a1 div a2

- val deli2 = fn : int * int * exn -> int

fun tabeliraj2 (zacetna, moja_napaka) =
   deli2(zacetna, zacetna-5, moja_napaka)::tabeliraj2(zacetna-1, moja_napaka)
   handle moja_napaka => [999]

- val tabeliraj2 = fn : int * exn -> int list

(***************************************************************)
(* izjema s parametrom *)
exception MatematicnaTezava of int*string

fun deli3 (a1, a2) =
   if a2 = 0 
   then raise MatematicnaTezava(a1, "deljenje z 0")
   else a1 div a2

fun tabeliraj3 zacetna =
   Int.toString(deli3(zacetna,zacetna-5)) ^ "  " ^ tabeliraj3(zacetna-1) 
   handle MatematicnaTezava(a1, a2) => a2 ^ " stevila " ^ Int.toString(a1)

1.3 Repna rekurzija, funkcije višjega reda, currying, delna aplikacija, mutacija, vzajemna rekurzija, moduli

Pregled

repna rekurzija
funkcije višjega reda
- funkcije kot argumenti funkcij
- funkcije, ki vračajo funkcije
- map/filter/fold
doseg vrednosti
currying, delna aplikacija
mutacija
določanje podatkovnih tipov
vzajemna rekurzija
moduli

1.3.1 Repna rekurzija

Repna rekurzija je bolj učinkovita od drugih oblik rekurzije.

Razlog:

(v splošnem): pri vsakem klicu funkcije se funkcijski okvir s kontekstom potisne na sklad; ko se funkcija zaključi, se kontekst odstrani s sklada
pri repni rekurziji se okvir samo zamenja z novim (prihranek na prostoru in času), ker kličoča funkcija konteksta ne potrebuje več

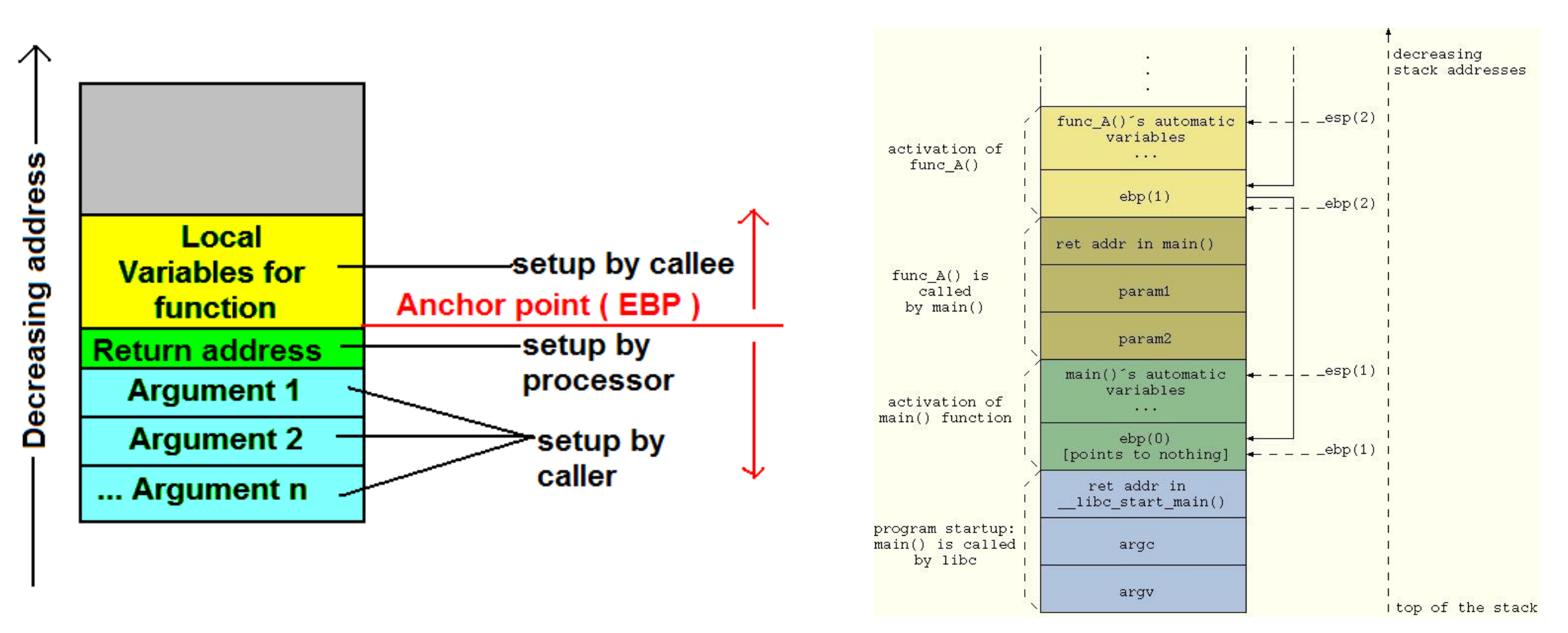
1.3.1.1 Izvedba rekurzije

Primer “navadne” rekurzije:

fun potenca (x,y)= if y=0 then 1 else x * potenca(x, y-1)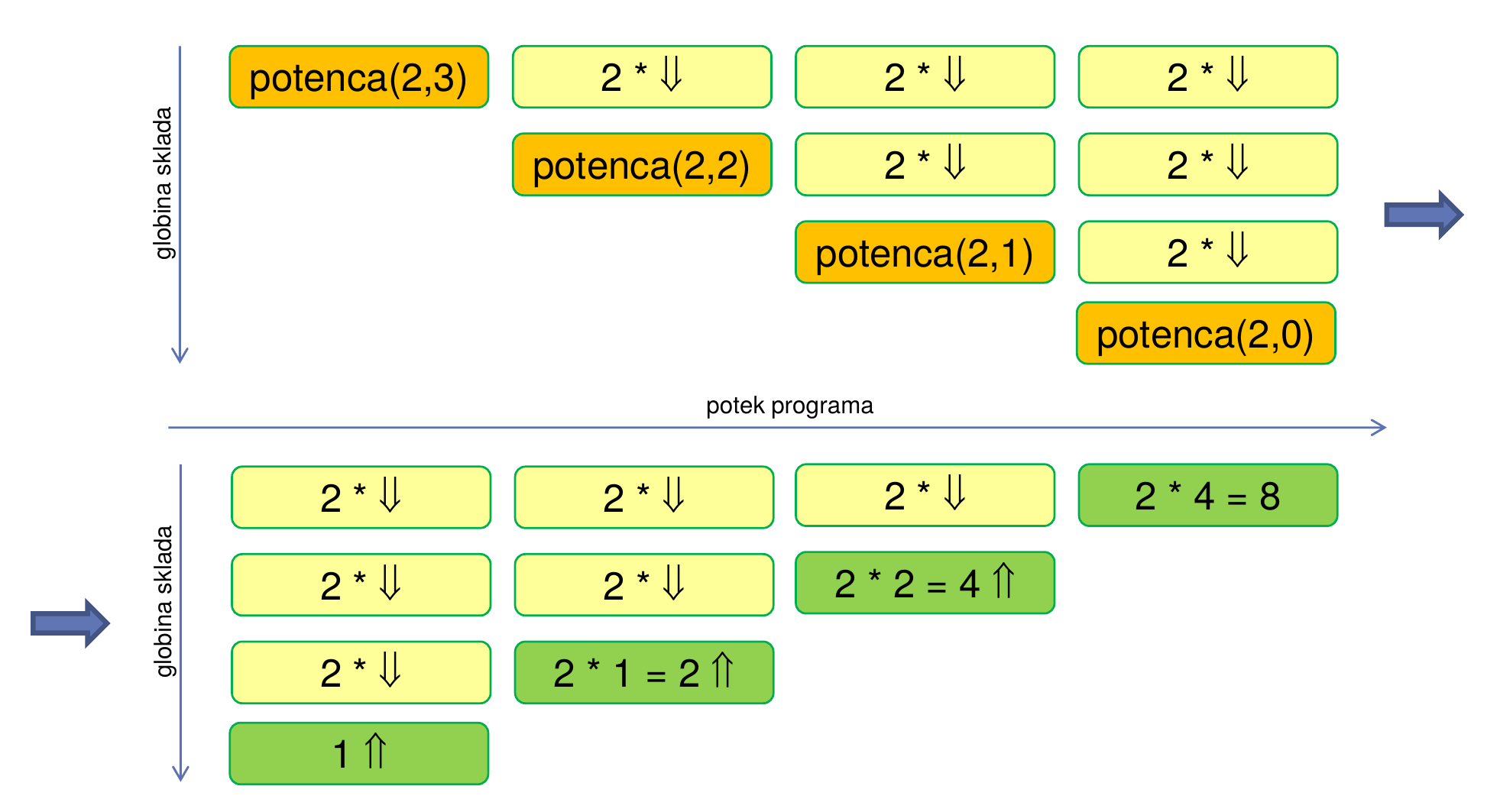

1.3.1.2 Drugačna implementacija

Alternativa: rekurzivna implementacija z lokalno pomožno funkcijo:

pomožna funkcija sprejema dodatni argument, imenovan akumulator
telo glavne funkcije vsebuje samo klic pomožne funkcije brez dodatnih operacij
klic pomožne funkcije v telesu glavne funkcije vsebuje začetno vrednost akumulatorja

fun potenca (x,y) =  
   if y=0 
   then 1 
   else x * potenca(x, y-1)

(* prevedba v repno rekurzijo *)
fun potenca_repna (x,y) =
   let
      fun pomozna (x,y,acc) =
         if y=0
         then acc
         else pomozna(x, y-1, acc*x)
   in
      pomozna(x,y,1)
   end

Izvedba programa:

1.3.1.3 Repna rekurzija - nadaljevanje

Repna rekurzija:

po izvedbi rekurzivnega klica v repu funkcije, ni potrebno izvesti več nobenih dodatnih operacij (množenje, seštevanje, …)
rep funkcije definiramo rekurzivno:
- v izrazu fun f p = e je telo e v repu
- v izrazu if e1 then e2 else e3 sta e2 in e3 v repu
- v izraz let b1 ... bn in e end je e v repu

Pri repni rekurziji programski jeziki optimizirajo izvajanje:

namesto hranjenja okvirja ga zamenjajo z okvirjem klicane funkcije
kličoča in klicana funkcija uporabljata isti prostor na skladu

Po učinkovitosti enakovredno zankam. Prevedba v repno rekurzijo ni vedno možna (obdelava dreves?).

Torej, dejanska izvedba funkcije z repno rekurzijo:

Primeri

Napiši naslednje funkcije, ki uporabljajo repno rekurzijo:

Funkcijo, ki obrne elemente v seznamu
Funkcijo, ki prešteje število pozitivnih elementov v seznamu
Funkcijo, ki sešteje elemente v seznamu

(***************************************************************)
(* 1. obrni elemente seznama *)
fun obrni sez =
   case sez of
      [] => []
      | x::rep => (obrni rep) @ [x] (* @ je operator za združevanje (konkatenacijo) seznamov *)

fun obrni_repna sez =
   let 
      fun pomozna(sez,acc) =
            case sez of
               [] => acc
               | x::rep => pomozna(rep, x::acc)
    in
        pomozna(sez,[])
    end

(***************************************************************)
(* 2. prestej pozitivne elemente *)
fun prestejpoz sez =
   case sez of
      [] => 0
      | g::rep => if g>=0 
                  then 1+ prestejpoz rep
                  else prestejpoz rep

fun prestejpoz_repna sez =
   let
      fun pomozna (sez, acc) =
         case sez of
            [] => acc
            | g::rep => if g>=0
                        then pomozna(rep, acc+1)
                        else pomozna(rep, acc)
   in
      pomozna(sez,0)
   end

// TODO: 3. primer

1.3.2 Funkcije višjega reda

Tudi funkcije so objekti (to pomeni: tudi funkcije so vrednosti, s katerimi lahko delamo enako kot z drugimi preprostimi vrednostmi)

koristno za ločeno programiranje pogostih operacij, ki jih uporabimo kot zunanjo funkcijo

> fun operacija1 x = x*x*x
> fun operacija2 x = x + 1
> fun operacija3 x = ~x
val operacija1 = fn : int -> int
val operacija2 = fn : int -> int
val operacija3 = fn : int -> int

funkcijam, ki sprejemajo ali vračajo funkcije, pravimo funkcije višjega reda (angl. higher-order functions)

> fun izvedi (pod, funkcija) =
      funkcija (pod+100)
val izvedi = fn : int * (int -> 'a) -> 'a

funkcije imajo funkcijsko ovojnico (angl. function closure) – struktura, v kateri hranijo kontekst, v katerem so bile definirane (vrednosti spremenljivk izven kličoče funkcije!)
```
> izvedi (2, operacija1);
val it = 1061208 : int
> izvedi (2, operacija2);
val it = 103 : int
> izvedi2 (2, operacija3);
val it = ~102 : int
```

1.3.2.1 Funkcije kot argumenti funkcij

Funkcije so lahko argumenti drugih funkcij ➔ bolj splošna programska koda.

fun nkrat (f, x, n) =
   if n=0
   then x
   else f(x, nkrat(f, x, n-1))

fun pomnozi(x,y) = x*y
fun sestej(x,y) = x+y
fun rep(x,y) = tl y

fun zmnozi_nkrat_kratka (x,n) = nkrat(pomnozi, x, n)
fun sestej_nkrat_kratka (x,n) = nkrat(sestej, x, n)
fun rep_nti_kratka (x,n) = nkrat(rep, x, n)

Brez funkcij kot argumenti funkcij:

(* ponavljajoca se programska koda: *)
fun zmnozi_nkrat (x,n) =  
   if n=0
   then x 
   else x * zmnozi_nkrat(x, n-1)

fun sestej_nkrat (x,n) =  
   if n=0 
   then x 
   else x + sestej_nkrat(x, n-1)

fun rep_nti (sez,n) =  
   if n=0 
   then sez 
   else tl (rep_nti(sez, n-1))

Funkcije višjega reda so lahko polimorfne (večja splošnost):

val nkrat = fn : ('a * 'a -> 'a) * 'a * int -> 'a

1.3.2.2 Funkcije, ki vračajo funkcije

Funkcije so lahko rezultat drugih funkcij.

Primer:

> fun odloci x =
      if x>10
      then (let fun prva x = 2*x in prva end)
      else (let fun druga x = x div 2 in druga end)

val odloci = fn : int -> int -> int

> odloci 12;
val it = fn : int -> int

> (odloci 12) 10;
val it = 20 : int

> (odloci 2) 20;
val it = 10 : int

Tip funkcije odloci je:

fn : int -> int -> int

Pri izpisu velja desna asociativnost, torej pomeni:

fn : int -> (int -> int)

1.3.2.2.1 Anonimne funkcije

Namesto ločenih deklaracij funkcij (fun), lahko funkcije deklariramo na mestu, kjer jih potrebujemo (brez imenovanja – anonimno).

Sintaksa predstavlja izraz in ne deklaracijo (fn namesto fun in => namesto =):

fn arg => telo

Primer uporabe: pri podajanju argumenta funkcijam višjega reda.

Funkcija je lokalna, imena dejansko ne potrebujemo:

fun zmnozi_nkrat (x,n) =
   nkrat(|let fun pomnozi (x,y) = x*y in pomnozi end|bg:orange| , x, n)

⬇ enakovredno, lepši zapis

fun zmnozi_nkrat (x,n) =
   nkrat(|fn (x,y) => x*y|bg:orange|, x, n)

Anonimnih funkcij ne moremo definirati rekurzivno - zakaj?

Anonimne funkcije ne morejo biti rekurzivne, ker nimajo reference nase (self-reference). Rekurzija zahteva, da se funkcija lahko sklicuje na svoj identifikator znotraj svoje definicije, kar pri anonimni funkciji ni mogoče, saj po definiciji nima imena.

1.3.2.2.2 Funkcije višjega reda - nadaljevanje

Funkcije, ki sprejemajo/vračajo funkcije.

Refaktorizacija kode:

fun nkrat (f, x, n) =
   if n=0
   then x
   else f(x, nkrat(f, x, n-1))

fun zmnozi_nkrat_mega (x,n) = nkrat(fn (x,y) => x*y, x, n)
fun sestej_nkrat_mega (x,n) = nkrat(fn(x,y) => x+y, x, n)
fun rep_nti_mega (x,n) = nkrat(fn(_,x)=>tl x, x, n)

S predavanj:

(* primer na seznamu - anon. fun. in izogib ovijanju funkcij v funkcije *)
fun prestej sez =
   case sez of 
      [] => 0
      | glava::rep => 1 + prestej rep

fun sestej_sez sez =
   case sez of 
      [] => 0
      | glava::rep => glava + sestej_sez rep

(* faktorizacija *)
fun predelaj_seznam (f, sez) =
   case sez of
      [] => 0
      | glava::rep => (f sez) + (predelaj_seznam (f,rep))

fun prestej_super sez = predelaj_seznam (fn x => 1, sez)
fun sestej_sez_super sez = predelaj_seznam(hd, sez)   (* hd namesto fn x => hd x !!! *)

1.3.2.3 Map/filter/fold

1.3.2.3.1 Funkcija Map

Preslika seznam v drugi seznam tako, da na vsakem elementu uporabi preslikavo f (ciljni seznam ima torej enako število elementov):

fun map (f, sez) =
   case sez of
      [] => []
      | glava::rep => (f glava)::map(f, rep)

Podatkovni tip funkcije map:

val map = fn : ('a -> 'b) * 'a list -> 'b list

Primer:

- map (fn x => Int.toString(2*x)^"a", [1,2,3,4,5,6,7]);
val it = ["2a","4a","6a","8a","10a","12a","14a"] : string list

1.3.2.3.2 Funkcija Filter

Preslika seznam v drugi seznam tako, da v novem seznamu ohrani samo tiste elemente, za katere je predikat (funkcija, ki vrača bool) resničen:

fun filter (f, sez) =
   case sez of
      [] => []
      | glava::rep => if (f glava)
                     then glava::filter(f, rep)
                     else filter(f, rep)

Podatkovni tip funkcije filter:

val filter = fn : ('a -> bool) * 'a list -> 'a list

Primer:

- filter(fn x => x mod 3=0, [1,2,3,4,5,6,7,8,9,10]);
val it = [3,6,9] : int list

Primeri:

Z uporabo map in filter:

Preslikaj seznam seznamov v seznam glav vgnezdenih seznamov:

- nal1 [[1,2,3],[5,23],[33,42],[1,2,5,6,3]];
val it = [1,5,33,1] : int list

Preslikaj seznam seznamov v seznam dolžin vgnezdenih seznamov:

- nal2 [[1,2,3],[5,23],[33,42],[1,2,5,6,3]];
val it = [3,2,2,5] : int list

Preslikaj seznam seznamov v seznam samo tistih seznamov, katerih dolžina je daljša od 2:

- nal3 [[1,2],[5],[33,42],[1,2,5,6,3]];
val it = [[1,2],[33,42],[1,2,5,6,3]] : int list list

Preslikaj seznam seznamov v seznam vsot samo lihih elementov vgnezdenih seznamov:
```
- nal4 [[1,2,3],[5,23],[33,42],[1,2,5,6,3]];
val it = [4,28,33,9] : int list
```

(* preslikaj seznam seznamov v seznam glav vgnezdenih seznamov *)
fun nal1 sez = map(hd, sez)

(* preslikaj seznam seznamov v seznam dolžin vgnezdenih seznamov *)
fun nal2 sez = map(prestej, sez)

(* preslikaj seznam seznamov v seznam samo tistih seznamov, katerih dolžina je daljša od 2 *)
fun nal3 sez = filter(fn x => (prestej x) >= 2, sez)

(* preslikaj seznam seznamov v seznam vsot samo lihih elementov vgnezdenih seznamov *)
fun nal4 sez =
   map(sestej_sez,
      map(
         fn el => filter(fn x => x mod 2 = 1, el),
         sez
      )
   )

1.3.2.3.3 Funkcija Fold

Znana tudi pod imenom reduce. Združi elemente seznama v končni rezultat. Na elementih seznama izvede funkcijo f, ki upošteva trenutni rezultat in vrednost naslednjega elementa.

fold(f, acc, [a,b,c,d]) (* izračuna *) f(d,f(c,f(b,f(a,acc))))

Primer: seštevanje seznama

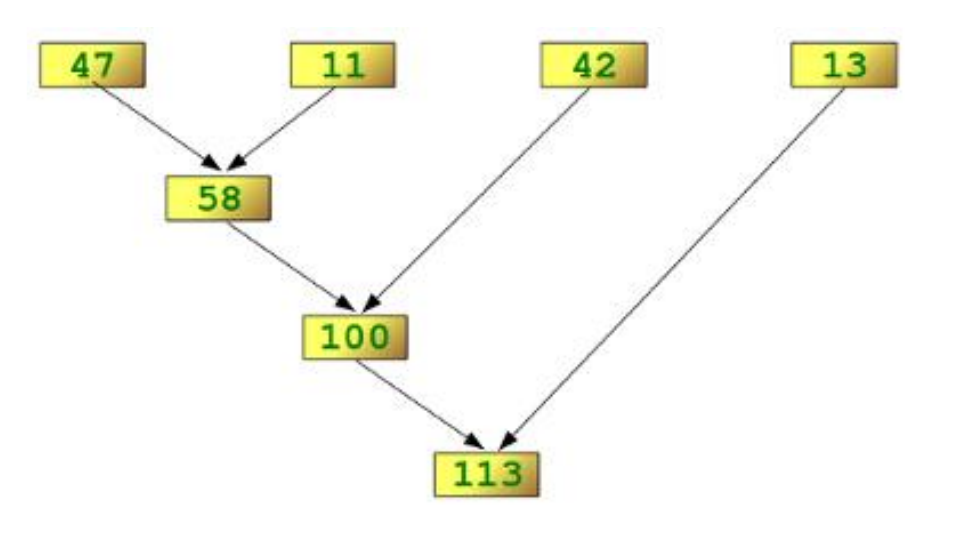
fun fold (f, acc, sez) =
   case sez of
      [] => acc
      | glava::rep => fold(f, f(glava, acc), rep)

Podatkovni tip funkcije fold:

val fold = fn : ('a * 'b -> 'b) * 'b * 'a list -> 'b

Primer (se navezuje na naslednje primere):

(* seštej elemente v seznamu *)
> fold(fn (x,y) => x+y, 0, [1,2,3,4,5]);
val it = 15 : int

(* dolžina seznama *)
> fold(fn (x,y) => y+1, 0, [1,2,3,4,5]);
val it = 5 : int

Primeri

Uporabi map/filter/fold za zapis naslednjih funkcij:

Seštej elemente v celoštevilskem seznamu.
```
fn : int list -> int
```
Preštej število elementov v seznamu.
```
fn : 'a list -> int
```
Vrni zadnji element v seznamu.
```
fn : 'a list -> 'a
```
Izračunaj skalarni produkt dveh vektorjev.
```
fn : int list list -> int
```
Vrni n-ti element v seznamu.
```
fn : int list * int -> int
```
Obrni elemente v seznamu.
```
fn : int list -> int list
```

(* PRIMER 1: vsota elementov *)
fun vsota_el sez = fold(fn (x,y) => x+y, 0, sez);  

(* PRIMER 2: dolžina seznama *) 
fun dolzina_sez sez = fold(fn (x,y) => y+1, 0, sez);

(* PRIMER 3: izberi zadnji element v seznamu *)
fun zadnji sez = fold (fn (x,y) => x, hd sez, sez)

(* PRIMER 4: skalarni produkt [a,b,c]*[d,e,f] = ab+be+cf *)
fun skalarni [v1, v2] =
   fold(fn (x,y) => x+y, 0, map(fn (e1,e2) => e1*e2, ListPair.zip(v1,v2)))
   | skalarni _ = raise Fail "napačni argumenti";

(* PRIMER 5: izberi nti element v seznamu *)
fun nti (sez, n) = 
   fold(fn((x,y),z) => y, ~1,
      filter(fn (x,y) => x=n,
         ListPair.zip (List.tabulate (List.length sez, fn x => x+1),
                     sez)
         )
      )

1.3.3 Doseg vrednosti

Funkcije kot prvo-razredni objekti so zmogljivo orodje. Definirati moramo semantiko pri določanju vrednosti spremenljivk v funkciji imamo dve možnosti:

1.3.3.1 Funkcijska ovojnica (angl. function closure)

Pri deklaraciji funkcije torej ni dovolj, da shranimo le programsko kodo funkcije, temveč je potrebno shraniti tudi trenutno okolje.

FUNKCIJSKA OVOJNICA = koda funkcije + trenutno okolje

Klic funkcije = evalvacija kode f v okolju env, ki sta del funkcijske ovojnice (f, env)

Vaja

Kaj je rezultat naslednjih deklaracij, upoštevajoč leksikalni in dinamični doseg?

val u = 1
fun f v =
   let
      val u = v + 1
   in
      fn w => u + v + w
   end
val u = 3
- val u = <hidden-value> : int
- val f = fn : int -> int -> int
- val u = 3 : int

val g = f 4 (* v=4 *)
- val g = fn : int -> int (* leksikalni: u=5; dinamičen: u=3 *)

val v = 5
- val v = 5 : int

val w = g 6 (* leksikalen: u=5, v=4; dinamičen: u=3, v=5; oboje: w=6 *)
- val w = 15 : int (* leksikalen: 5+4+6=15; dinamičen: 3+5+6=14 *)

leksikalni: 15

dinamični: 14 (TODO: verify)

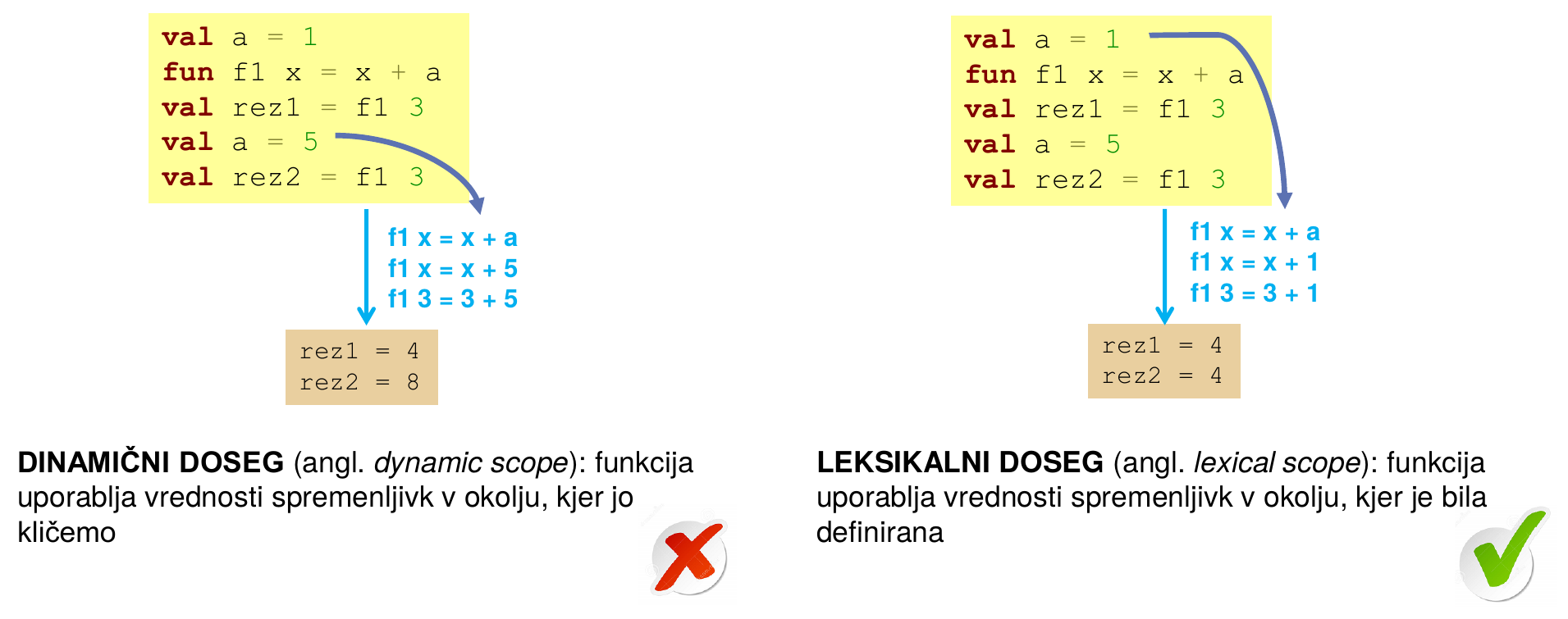
1.3.3.2 Leksikalni doseg

Funkcija uporablja vrednosti spremenljivk v okolju, kjer je definirana. V zgodovini sta bili v programskih jezikih uporabljeni obe možnosti, danes prevladuje odločitev, da uporabljamo leksikalni doseg.

Leksikalni doseg je bolj zmogljiv: ➔ razlogi v nadaljevanju

Dinamičen doseg:

pogost pri skriptnih jezikih (Lisp, bash, Logo, delno Perl)
včasih bolj primeren (proženje izjem, izpisovanje v statične datoteke, …)
nekateri sodobni jeziki imajo “posebne” spremenljivke, ki hranijo vrednosti v dinamičnem dosegu

1.3.3.2.1 Prednosti leksikalnega dosega

Imena spremenljivk v funkciji so neodvisna od imen zunanjih spremenljivk:

Drugače povedano: neodvisnost lokalnih spremenljivk od zunanjega okolja.

fun fun1 y =
   let val |x|color:red| = 3
   in fn z => |x|color:red| + y + z
   end

val a1 = (fun1 7) 4
val |x|color:red| = 42 (* nima vpliva *)
val a2 = (fun1 7) 4

Funkcija je neodvisna od imen uporabljenih spremenljivk

Drugače povedano: neodvisnost funkcije od argumentov.

fun fun1 y =
   let
      val |x|color:red| = 3
   in
      fn z => |x|color:red| + y + z
   end

⬌

fun fun2 y =
   let
      val |q|color:red| = 3
   in
      fn z => |q|color:red| + y + z
   end

Zgornji funkciji sta enakovredni

val x = 42 (* ne igra nobene vloge *)
val a1 = (fun1 7) 4
val a2 = (fun2 7) 4

Tip funkcije lahko določimo ob njeni deklaraciji:

Drugače povedano: podatkovni tip lahko določimo pri deklaraciji funkcije.

val x = 1
fun fun3 y = 
   let val x = 3
   in fn z => x+y+z end    (* int -> int -> int *)
val x = false              (* NE VPLIVA NA PODATKOVNI TIP KASNEJŠEGA KLICA! *)
val g = fun3 10            (* vrne fn, ki prišteje 13 *)
val z = g 11               (* 13 + 11 = 24 *)

Ovojnica shrani podatke, ki jih potrebuje za kasnejšo izvedbo:

Drugače povedano: ovojnica shrani (“zapeče”) interne podatke za klic funkcije.

fun filter (f, sez) =
   case sez of
      [] => []
      | x::rep => if (f x)
                     then x::filter(f, rep)
                     else filter(f, rep)
fun vecjiOdX x = fn y => y > x
fun brezNegativnih sez = filter(vecjiOdX ~1, sez)

Glej x in vecjiOdX ~1.

POZOR:

x je neodvisen od x-a v funkciji filter; če ne bi bil, bi primerjali elemente same s sabo (x, ki je argument predikata in x, ki nastopa kot glava v funkciji filter
prvi argument v klicu filter() — vecjiOdX ~1 — je ovojnica, ki hrani shranjen interni x, ki je neodvisen od x v filter()

1.3.4 Currying (delna aplikacija)

1.3.4.1 Currying

Currying – ime metode, naziv dobila po matematiku z imenom Haskell Curry.

Spomnimo se: funkcije sprejemajo natanko en argument, če želimo podati več vrednosti v argumentu, smo jih običajno zapisali v terko.

Alternativna možnost: če imamo več argumentov, naj funkcija sprejme samo en argument in vrne funkcijo, ki sprejme preostanek argumentov (nadaljevanje na enak način).

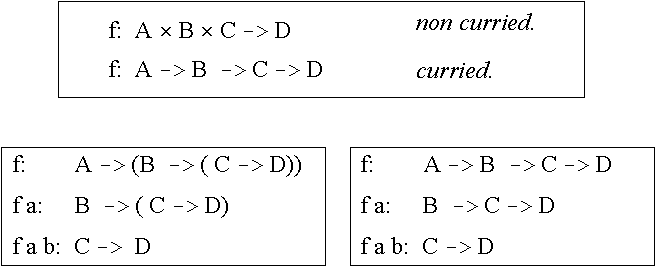
“Stari način”: funkcija, ki sprejema terko argumentov:

fun vmejah_terka (min, max, sez) =
   filter(fn x => x>=min andalso x<=max, sez)

Currying: funkcija, ki vrača funkcijo…

fun vmejah_curry min = (* različica, ki uporablja currying *)
   fn max =>
      fn sez =>
         filter(fn x => x>=min andalso x<=max, sez)

Klici:

vmejah_terka (5, 15, [1,5,3,43,12,3,4]);

(((vmejah_curry 5) 15) [1,5,3,43,12,3,4]);

1.3.4.1.1 Currying: sintaktične olepšave

Deklaracijo funkcije:

fun vmejah_curry min =
   fn max =>
      fn sez =>
         filter(fn x => x>=min andalso x<=max, sez)

lahko lepše zapišemo s presledki med argumenti:

fun vmejah_lepse min max sez =
   filter(fn x => x>=min andalso x<=max, sez)

Klic:

(((vmejah_curry 5) 15) [1,5,3,43,12,3,4]);

lahko lepše zapišemo brez oklepajev:

vmejah_curry 5 15 [1,5,3,43,12,3,4];

1.3.4.2 Delna aplikacija funkcij

Ko uporabljamo currying, lahko pri klicu funkcije podamo manj argumentov, kot jih funkcija ima.

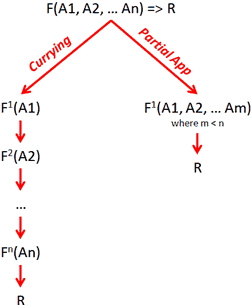
Rezultat: delna aplikacija funkcije oz. funkcija, ki “čaka” na preostale argumente.

Prednost: klic lahko posplošimo v drugo funkcijo.

Sintaksa: spomnimo se, da lahko zapišemo:

val f = g

če sta f in g funkciji; ta zapis je enakovreden (sintaktično slabše):

fun f x = g x

Primer:

(* PRIMER 1: vrne samo števila od 1 do 10 *)
val prva_desetica = vmejah_curry 1 10;

- prva_desetica [1,14,3,23,4,23,12,4];
val it = [1,3,4,4] : int list

(* PRIMER 2: obrne vrstni red argumentov *)
fun vmejah2 sez min max = vmejah_lepse min max sez;
(* določi zgornjo mejo fiksnega seznama *)
val zgornja_meja = vmejah2 [1,5,2,6,3,7,4,8,5,9] 1;

(* PRIMER 3. primeri z uporabo map/filter/foldl *)
val povecaj = List.map (fn x => x + 1);
val samoPozitivni = List.filter (fn x => x > 0);
val vsiPozitivni = List.foldl (fn (x,y) => y andalso (x>0)) true;  (* pozor, vrstni red arg v fn! *)

Zato, da lahko izvajamo delno aplikacijo, vgrajene funkcije List.map, List.filter in List.fold uporabljajo currying:

(* poveča vse elemente v seznamu za 1 *)
val povecaj = List.map (fn x => x + 1);

V SML/NJ je bolj učinkovita uporaba funkcij s terkami kot če uporabljamo currying. Zakaj?

V SML/NJ je uporaba funkcij s terkami bolj učinkovita, ker se curried funkcije interno prevedejo v gnezdene funkcije, kjer se za vsak delni klic ustvari nov closure na kopici (heap). Pri funkcijah s terkami se izvede samo en funkcijski klic brez dodatnih alokacij, medtem ko curried funkcije zahtevajo več klicev in alokacij.

Slednje ne velja nujno tudi za druge programske jezike (optimizacija kode v prevajalniku).

Pomoč v REPL glede argumentov funkcij:

> structure X = ListPair;  (* povprašamo po nazivu knjižnice *)
structure X : LIST_PAIR

> signature X = LIST_PAIR; (* zahtevamo izpis povzetka *)

Prevedba med zapisi funkcij

Zapis s terko ⬌ currying:

fun curry f x y = f (x,y)
fun uncurry f (x,y) = f x y

Zamenjava vrstnega reda argumentov:

fun zamenjaj f x y = f y x

1.3.5 Mutacija

1.3.5.1 Mutacija vrednosti

Kot prednost funkcijskega programiranja smo omenili izogibanje “stranskim učinkom” programa, kot je spreminjanje vrednosti spremenljivkam.

Wiki (side effects):

In the presence of side effects, a program’s behavior depends on history; that is, the order of evaluation matters. Understanding and debugging a function with side effects requires knowledge about the context and its possible histories.

Kje tiči prednost v tem?

preprosto ponovljivo testiranje funkcij (neodvisne od konteksta)
neodvisnost naše kode od implementacije algoritmov in podatkovnih struktur

1.3.5.2 Neodvisnost od implementacije

Primer: funkcija za združevanje dveh seznamov:

(* združi seznama sez1 in sez2 v skupni seznam *)
fun zdruzi_sez sez1 sez2 =
   case sez1 of
      [] => sez2
      | g::rep => g::(zdruzi_sez rep sez2)

val s1 = [1,2,3]
val s2 = [4,5]

val rezultat = zdruzi_sez s1 s2

Rešitev zadnjega klica je (očitno) seznam [1,2,3,4,5], vendar pa: ali je združevanje uporablja referenci na s1 in s2 ali kopira elemente?

referenca:
kopija:

Ali je to sploh pomembno? (v nadaljevanju)

SML sicer uporablja reference (varčevanje s prostorom), vendar to ni pomembno, ker brez mutacij ne moremo povzročiti nepričakovanih rezultatov, kot je ta:

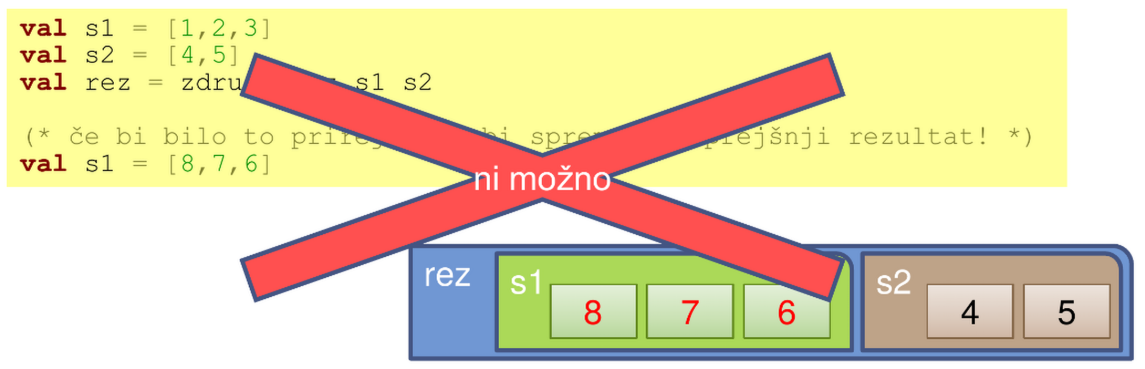
V jezikih z mutacijo je zgornje vir številnih nepredvidenih semantičnih napak (Java?)

Resnica: SML tudi lahko uporablja mutacijo!

1.3.5.3 Mutacija - nadaljevanje

Priročen pristop, kadar potrebujemo spremenljivo globalno stanje v programu za mutacijo vpeljemo novi podatkovni tip t ref (t je poljubni tip):

ref e    (* izdelava spremenljivke *)
e1 := e2 (* sprememba vsebine *)
!e       (* vrne vrednost *)

Primer:

> val x = ref 15;
val x = ref 15 : int ref

> val y = ref 2;
val y = ref 2 : int ref

> (!x)+(!y);
val it = 17 : int

> x:=7;
val it = () : unit

> (!x)+(!y);
val it = 9 : int


(* PRIMER: nepričakovani učinek *)

> val x = ref "zivjo";
val x = ref "zivjo" : string ref

> val y = ref 2013;
val y = ref 2013 : int ref

> val z = (x, y)
> val _ = x:="kuku";
val z = (ref "kuku",ref 2013) : string ref * int ref

> val w = (x,y);
val w = (ref "kuku",ref 2013) : string ref * int ref


(* PRIMER: uporaba mutacije *)
val zgodovina = ref ["zacetek"];
val sez = ref [1,2,3]

fun pripni element  =
  (zgodovina:= (!zgodovina) @ ["pripet " ^ Int.toString(element)]
  ;
      sez := (!sez)@[element] )

fun odpni () =
  case (!sez) of
      [] => []
      | g::r => (zgodovina:= (!zgodovina) @ ["odstranjen " ^ Int.toString(g)]
         ; sez := r
         ; [g])


(* *)
> pripni 2;
val it = () : unit

> pripni 242;
val it = () : unit

> zgodovina;
val it = ref ["zacetek","pripet 2","pripet 242"] : string list ref

> odpni ();
val it = [1] : int list

> odpni ();
val it = [2] : int list

> zgodovina;
val it = ref ["zacetek","pripet 2","pripet 242","odstranjen 1","odstranjen 2"]
  : string list ref

(* Pazi! *)
> val y = ref [];
stdIn:47.5-47.15 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val y = ref [] : ?.X1 list ref

Mutacije ne uporabljamo, razen če ni nujno potrebno: povzročajo stranske učinke in težave pri določanju podatkovnih tipov! (→ kasneje več o tem).

1.3.6 Določanje podatkovnih tipov (angl. type inference)

Cilj: vsaki deklaraciji (zaporedoma) določiti tip, ki bo skladen s tipi preostalih deklaracij.

Tipizacija glede na statičnost:

statično tipizirani jeziki (ML, Java, C++, C#): preverjajo pravilnost podatkovnih tipov in opozorijo na napake v programu pred izvedbo
dinamično tipizirani jeziki (Racket, Python, JavaScript, Ruby): izvajajo manj (ali nič) preverb pravilnosti podatkovnih tipov, večino preverjanj se izvede pri izvajanju

Tipizacija glede na implicitnost:

implicitno tipiziran jezik (ML, JavaScript): podatkovnih tipov nam ni potrebno eksplicitno zapisati (kdaj smo jih že morali pisati?)
eksplicitno tipiziran jezik (Java, C++, C#): potreben ekspliciten zapis tipov

Ker je ML implicitno tipiziran jezik, ima vgrajen mehanizem za samodejno določanje podatkovnih tipov.

1.3.6.1 Postopek

Postopek določanja podatkovnega tipa za vsako deklaracijo:

Za deklaracijo (val ali fun) naredi seznam omejitev.
Analiziraj omejitve in določi tipe.
Rezultat:
1. če so omejitve v protislovju → vrni napako
2. če iz presplošnih omejitev ni možno določiti konkretnega tipa → uporabi zanje spremenljivko (za polimorfizem: 'a, 'b, …)
3. uporabi omejitev vrednosti (angl. value restriction) (o tem kasneje)

Primer:

fun f (q, w, e) =          (* 1. f: 'a * 'b * 'c -> 'd *)
                           (* 3. f: ('f * 'g) list * 'b * 'c -> 'd *)
                           (* 5. f: ('f * 'g) list * bool list * 'c -> 'd *)
                           (* 8. f: ('f * int) list * bool list * 'c -> int *)
   let val (x,y) = hd(q)   (* 2. 'a = 'e list; 'e = ('f * 'g); 'a = ('f * 'g) list *)
   in if hd w              (* 4. 'b = 'h list; 'h = bool; 'b = bool list *)
      then y mod 2         (* 6. y: int; 'd = int *)
      else y*y             (* 7. skladno s 6 velja y: int; 'd = int *)
   end

Dodatna primera s predavanj:

(* PRIMER 1 *)
fun fakt x =                (* 1.   fakt: 'a -> 'b *)
                            (* 3.   fakt : int -> __ *)
                            (* 6.   fakt: int -> int *)
    if x = 0                (* 2.   x: 'a; 'a = int, zato da primerjava z 0 uspe *)
    then 1                  (* 4.   rezultat funkcije je 'b = int *)
    else x*(fakt (x-1))     (* 5.   mora biti skladno s 4; x: int, (fakt x): int, 'b = int *)


(* PRIMER 2 *)

(* fun compose (f,g) = fn x => f (g x)   *)
(* val koren_abs = compose (Math.sqrt, abs);
      je enakovredno kot
   val koren_abs2 = Math.sqrt o abs;  *)

fun compose1 (f,g) =   (* 1.  f: 'a -> 'b;  g: 'c -> 'd *; 
                              compose: ('a -> 'b) * ('c -> 'd) -> 'e                         *)
                       (* 6.  compose: ('a -> 'b) * ('c -> 'a) -> ('c -> 'b)                 *)
    fn x => f (g x)    (* 2.  x: 'c, 'e: 'c -> NEKAJ                                         *)
                       (* 3.                   g: 'c -> 'd;  g x: 'd                         *)
                       (* 4.                   f: 'a -> 'b;  f (g x) = 'b  --> velja 'd=='a! *)
                       (* 5.         'e: 'c -> 'b                                            *)

1.3.6.2 Premislek…

Če programski jezik izvaja določanje podatkovnega tipa, lahko uporablja spremenljivke tipov ('a, 'b, 'c, …) ali pa tudi ne.

Kakšna je prednost, če uporablja?

Glavna prednost uporabe spremenljivk tipov ('a, 'b, 'c, itd.) pri določanju podatkovnih tipov je podpora polimorfizmu, kar omogoča pisanje generičnih funkcij, ki lahko delujejo z različnimi tipi podatkov. To bistveno zmanjša potrebo po podvajanju kode, saj ena funkcijska definicija lahko dela z več različnimi tipi, hkrati pa ohranja tipno varnost, ker se skladnost tipov še vedno preverja v času prevajanja. Brez spremenljivk tipov bi morali pisati ločene funkcije za vsak podatkovni tip posebej.

Vendar pa: kombinacija polimorfizma in mutacije lahko prinese težave pri določanju tipov, če bi pomenila spremembo določenega podatkovnega tipa:

legalen primer (brez polimorfizma):

> val sez = ref [1,2,3];   (* sez je tipa int list ref *)
val sez = ref [1,2,3] : int list ref

> sez := (!sez) @ [4,5];
> !sez;
val it = [1,2,3,4,5] : int list

problematičen primer (uporablja polimorfen tip):

(* tole dejansko ne dela, ker je `ref []` dummy type *)
val sez = ref [];     (* sez je tipa 'a list ref *)
sez := !sez @ [5];    (* v seznam dodamo int *)     |cross|
sez := !sez @ [true]; (* |pokvari pravilnost tipa seznama!|color:red| *)

Rešitev: spremenljivka ima lahko polimorfen tip samo, če je na desni strani deklaracije vrednost (konstanta), spremenljivka ali nepolimorfna funkcija. To imenujemo omejitev vrednosti.

ref ni vrednost/spremenljivka, ampak funkcija (konstruktor)

1.3.6.3 Omejitev vrednosti

Deklaracije spremenljivk polimorfnih tipov dopustimo le, če je na desni strani vrednost (konstanta), spremenljivka ali nepolimorfna funkcija.

Odgovor ML:

ML določi spremenljivkam neveljaven tip (dummy type), ki ga ne moremo uporabljati za funkcijske klice

> val sez = ref [];
stdIn:10.5-10.17 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val sez = ref [] : ?.X1 list ref

Dve možni rešitvi:

ročna opredelitev podatkovnih tipov

ovijanje deklaracije vrednosti v deklaracijo funkcije (za njih ne velja omejitev vrednosti):

> val mojaf1 = map (fn x => 1);
stdIn:11.5-11.17 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)

> mojaf1 [1,2,3];
stdIn:18.1-18.15 Error: operator and operand don't agree [literal]
   operator domain: ?.X1 list
   operand:          int list

> fun mojaf2 sez = map (fn x => 1) sez;
val mojaf2 = fn : 'a list -> int list

> mojaf2 [1,2,3];
val it = [1,1,1] : int list

Koda s predavanj:

(*  *)
> val sez = ref [];                  (* NE DELUJE: omejitev vrednosti *)
stdIn:1.6-1.18 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val sez = ref [] : ?.X1 list ref

> val xx = ref NONE;                 (* NE DELUJE: omejitev vrednosti *)
stdIn:2.5-2.18 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val xx = ref NONE : ?.X1 option ref

> val xxx = ref []: int list ref;    (* REŠITEV 1: opredelimo podatkovne tipe *)
val xxx = ref [] : int list ref

> val mojaf = map (fn x => x+1);     (* ni polimorfna, deluje *)
val mojaf = fn : int list -> int list

> val mojaf1 = map (fn x => 1);      (* težava: polimorfizem + klic funkcije map *)
stdIn:5.5-5.29 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val mojaf1 = fn : ?.X1 list -> int list

> fun mojaf2 sez = map (fn x => 1) sez     (* REŠITEV 2: ovijemo vrednost v funkcijo *)
val mojaf2 = fn : 'a list -> int list

> mojaf [1,2,3]
val it = [2,3,4] : int list

> mojaf1 [1,2,3]
stdIn:10.1-10.15 Error: operator and operand do not agree [overload conflict]
  operator domain: ?.X1 list
  operand:         [int ty] list
  in expression:
    mojaf1 (1 :: 2 :: 3 :: nil)

1.3.7 Vzajemna rekurzija

Omogočati uporabo funkcij in podatkovnih tipov, ki so deklarirani za trenutno deklaracijo.

fun fun1 par1 = <telo>
|and|bg:red| fun2 par2 = <telo>
|and|bg:red| fun3 par3 = <telo>

datatype tip1 = <definicija>
|and|bg:red| tip2 = <definicija>
|and|bg:red| tip3 = <definicija>

Primer:

fun sodo x =
   if x=0
   then true
   else liho (x-1)
|and|bg:red| liho x =
   if x=0
   then false
   else sodo (x-1)

Primer s predavanj:

(* rekurzija v podatkovnih tipih *)
datatype zaporedje1 = A of zaporedje2 | Konec1
     and zaporedje2 = B of zaporedje1 | Konec2

A (B (A (B (A Konec2))));

(* ideja za končni avtomat, ki sprejema nize oblike [1,2,1,2,...] *)

V praksi uporabno za opisovanje stanj končnih avtomatov.

Izpitna naloga 2013/14

V jeziku SML napiši program check, ki preverja pravilnost vhodnega seznama sez. Za vhodni seznam morajo veljati naslednja pravila:

program naj sprejme prazen seznam,
seznam hrani vrednosti podatkovnega tipa datatype datum = A of int | B of int list
v seznamu se izmenjujeta podatka, narejena s konstruktorjem A in konstruktorjem B,
seznam se mora obvezno začeti z elementom, ki je narejen s konstruktorjem A in se lahko konča s poljubnim elementom (konstruktor A ali B),
seznami tipa int list, ki so argument konstruktorja B, vsebujejo elemente z vrednostima 3 in 4,
seznami tipa int list, ki so argument konstruktorja B, se morajo vedno končati na 4,njihov začetek pa ni pomemben.

Primeri:

- check [A 1, B [3,4], A 3];
val it = true : bool
- check [A 9, B [3,4], A 4, B [4,3,4,3,4], A 2, B [4]];
val it = true : bool
- check [B [3,4], A 1, B [4,3]];
val it = false : bool      (* has to start with A *)
- check [A 1, B [3,4,3]];
val it = false : bool      (* list given with B has to end with 4 *)

Rešitev:

datatype 'a podatek = A of int 
                      | B of int list

fun check nekej =
  case nekej of 
       A(_)::rep => check2 rep 
     | B(_)::_ => false
     | [] => true
and check2 nekej =
  case nekej of 
       [] => true
     | A(_)::_ => false
     | B(sez)::rep => check rep andalso check3 sez
and check3 seznam =
  check4 seznam andalso check5 seznam
and check4 seznam =
  case seznam of
      [] => false
     | glava::rep => if glava = 3 then true else check4 rep
and check5 seznam =
  case seznam of
      [] => false
     | zadnji::[] => if zadnji = 4 then true else false
     | _::rep => check5 rep

// TODO: verify

1.3.8 Moduli

Omogočajo:

organiziranje programske kode v smiselne celote
preprečevanje senčenja (isto ime je lahko deklarirano v več modulih)

Znotraj modula se sklicujemo na deklarirane objekte enako, kot smo se v prej v “zunanjem” okolju (brez posebnosti). Iz “zunanjega” okolja se na deklaracije v modulu sklicujemo z uporabo predpone “ImeModula.ime”.

Sintaksa za deklaracijo modula:

structure MyModule =
|struct|bg:red|
   <deklaracije val, fun, datatype, ...>
|end|bg:red|

structure Nizi =
struct
   val prazni_niz = ""
   fun prvacrka niz =
      hd (String.explode niz)
end

Primer s predavanj:

(* Modul za delo z nizi *)

structure Nizi =
struct
   val prazni_niz = ""

   fun dolzina niz =
      String.size niz

   fun prvacrka niz =
      hd (String.explode niz)

   fun povprecnadolzina seznam_nizov =
      Real.fromInt (foldl (fn (x,y) => (String.size x)+y) 0 seznam_nizov)
      /
      Real.fromInt (foldl (fn (_,y) => y+1) 0 seznam_nizov)
end

1.3.8.1 Javno dostopne deklaracije

Modulu lahko določimo, katere deklaracije so na razpolago “javnosti” in katere so zasebne (public in private v Javi?).

Seznam javnih deklaracij strnemo v podpis modula (signature), nato podpis pripišemo modulu.

signature PolinomP =          (* |deklaracija podpisa|color:cornflowerblue| *)
sig
   datatype polinom = Nicla | Pol of (int * int) list 
   val novipolinom : int list -> polinom
   val mnozi : polinom -> int -> polinom
   val izpisi : polinom -> string
end

(* |podpis pripišemo modulu; uporabimo operator :>|color:red| *)
structure Polinom |:> PolinomP|bg:orange| =
|struct|bg:orange|
   ... deklaracije ...
|end|bg:orange|

V podpisu določimo samo podatkovne tipe deklaracij (type, datatype, val, exception). Podpis mora biti skladen z vsebino modula, sicer preverjanje tipov ne bo uspešno.

Primera s predavanj:

(* Modul za delo s polinomi *)

(* podpisi *)
signature PolinomP2 =
sig
    type polinom
    val novipolinom : int list -> polinom
    val izpisi : polinom -> string
end

signature PolinomP3 =
sig
    type polinom
    val Nicla : polinom
    val novipolinom : int list -> polinom
    val izpisi : polinom -> string
end

1.3.8.2 Skrivanje implementacije

Uporaba podpisov modulov je koristna, ker z njim skrivamo implementacijo, kar je lastnost dobre in robustne programske opreme!

S skrivanjem implementacije dosežemo:

Uporabnik ne pozna načina implementacije operacij; lahko jo tudi kasneje spremenimo brez vpliva na preostalo kodo.
Uporabniku onemogočimo, da uporablja modul na napačen način.

Primer

Denimo, da specificiramo naslednje želje/zahteve glede uporabe:

za izdelavo novega polinoma naj se uporablja funkcija novipolinom
koeficienti polinoma so zapisani v padajočem vrstnem redu glede na potenco neodvisne spremenljivke
vse potence neodvisne spremenljivke so pozitivne
če je koeficient enak 0, ga ne hranimo
želimo, da funkcija za množenje ni vidna navzven, je pa na razpolago (morebitnim) internim funkcijam

signature PolinomP =
sig
   datatype polinom = Nicla | Pol of (int * int) list
   val novipolinom : int list -> polinom
   val mnozi : polinom -> int -> polinom  (* odstranimo? *)
   val izpisi : polinom -> string
end

Če odstranimo funkcijo mnozi iz podpisa, ali potem ta podpis ustreza zgornji specifikaciji?

žal ne… poglejmo si primer

(* modul *)
structure Polinom :> PolinomP3 =
struct

datatype polinom = Pol of (int * int) list | Nicla;

fun novipolinom koef = 
   let fun novi koef stopnja =
      case koef of
         [] => []
         | g::r => if g<>0
                  then (stopnja-1,g)::(novi r (stopnja-1))
                  else (novi r (stopnja-1))
   in
      Pol (novi koef (List.length koef))
   end

fun mnozi pol konst =
   case pol of
      Pol koef => if konst = 0
                  then Nicla
                  else Pol (map (fn (st,x) => (st,konst*x)) koef)
      | Nicla => Nicla

fun izpisi pol =
   case pol of
      Pol koef => let val v_nize = (map (fn (st,x) => (if st=0 
                                                      then Int.toString(x) 
                                                      else Int.toString(x) ^ "x^" ^ Int.toString(st))) koef)
                  in foldl (fn (x,acc) => (acc ^ " + " ^ x))
                           (hd v_nize)
                           (tl v_nize)
                  end
      | Nicla =>  "0"
end


(* *)
- Polinom.mnozi (Polinom.novipolinom [7,6,0,0,0,4]) 2;
val it = Pol [(5,14),(4,12),(0,8)] : Polinom.polinom
-  Polinom.mnozi (Polinom.novipolinom [7,6,0,0,0,4]) 0;
val it = Nicla : Polinom.polinom
- Polinom.mnozi (Polinom.Nicla) 3;
val it = Nicla : Polinom.polinom
- Polinom.izpisi (Polinom.mnozi (Polinom.novipolinom [7,6,0,0,0,4]) 2);
val it = "14x^5 + 12x^4 + 8" : string


(* uporabnik krši pravila uporabe *)
- Polinom.izpisi (Polinom.Pol [(3,1),(1,2),(16,0),(~5,3)]);
val it = "1x^3 + 2x^1 + 0x^16 + 3x^~5" : string

1.3.8.3 Skrivanje podrobnosti

Uporabnik lahko kvari delovanje, predvideno v specifikaciji (glej primer):

korak:

Skrijemo funkcijo za množenje:

signature PolinomP =
sig
   datatype polinom = Nicla
      | Pol of (int * int) list
   val novipolinom : int list -> polinom
   val izpisi : polinom -> string
end

korak:

Definiramo abstraktni podatkovni tip, ki ne razkriva podrobnosti implementacije uporabniku:
- skrijemo, da je polinom datatype
- uporabnik še vedno lahko računa s polinomi
```
signature PolinomP2 =
sig
   |type polinom|bg:red|
   val novipolinom : int list -> polinom
   val izpisi : polinom -> string
end
```

korak:

Vendar pa ni nič narobe, če razkrijemo samo del podatkovnega tipa (vrednost Nicla) in skrijemo samo konstruktor Pol:

signature PolinomP3 =
sig
   type polinom
   |val Nicla : polinom|bg:red|
   val novipolinom : int list -> polinom
   val izpisi : polinom -> string
end

1.3.8.4 Ustreznost modula in podpisa

Podpis lahko uspešno pripišemo modulu (Modul :> podpis), če velja:

Vsi ne-abstraktni tipi, ki smo jih navedli v podpisu, morajo biti implementirani v modulu (datatype).
Vsi abstraktnih tipi iz podpisa (implementirani s type) so implementirani v modulu (s type ali datatype).
Vsaka deklaracija vrednosti (val) v podpisu se nahaja v modulu (vendar pa je lahko v modulu bolj splošnega tipa).
Vsaka izjema (exception) v podpisu se nahaja tudi v modulu.

1.3.9 Dodatno (`infix`) (ni na prosojnicah)

V Standard ML (SML) je infix ključna beseda, ki se uporablja za deklaracijo, da se funkcija uporablja kot infiksni operator. To pomeni, da se funkcija kliče tako, da je nameščena med svojima argumentoma (namesto da bi jo zapisali v obliki predpone, npr. f(x, y)). To omogoča bolj naraven zapis za določene operacije, podobno kot pri aritmetičnih operatorjih (npr. +, *).

1.3.9.1 Delovanje

Deklaracija:

Z infix določimo, da se funkcija uporablja kot infiksni operator. Opcijsko lahko navedemo tudi prioriteto (število med 0 in 9; privzeto je 0). Višja števila pomenijo višjo prioriteto (npr. infix 7 *).
```
infix 5 add  (* Funkcijo 'add' uporabljajmo kot infiksni operator s prioriteto 5 *)
```
Uporaba:

Funkcijo lahko nato kličemo med argumentoma, ne da bi uporabili oklepaje ali vejice:
```
val rezultat = 3 add 5  (* Namesto add(3, 5) *)
```

Primer:

(* Definirajmo funkcijo, ki združi dva niza z "-" *)
fun combine (a, b) = a ^ "-" ^ b;

(* Deklarirajmo jo kot infiksni operator s prioriteto 6 *)
infix 6 combine;

(* Uporaba kot infiksnega operatorja *)
> val result = "hello" combine "world";
"hello-world"

Pomembne točke:

Prioriteta: Določa vrstni red izvajanja operacij. Na primer, infix 7 * pomeni, da ima operator * višjo prioriteto kot + (ki ima privzeto 0).
Asociativnost: Privzeto so infiksni operatorji levo asociativni (npr. 3 + 4 + 5 se obravnava kot (3 + 4) + 5). Za desno asociativnost uporabi infixr.
Uporaba brez deklaracije: Če funkcijo želito uporabiti kot infiksni operator samo enkrat, lahko uporabimo op (npr. 3 op + 4).

1.3.9.2 Uporabnost

Infiksni zapis je intuitivnejši za operacije, ki delujejo na dveh argumentih (npr. matematične operacije, združevanje struktur). Na primer, x + y je berljivejše od +(x, y). Z infix lahko svoje funkcije prilagodimo tej sintaksi.

1.4 Racket, dinamično tipiziranje, lokalno okolje, zakasnjena evalvacija, memoizacija, makro sistem

Pregled snovi do sedaj

paradigme programiranja (funkcijsko, objektno, usmerjeno, …)
sintaksa, semantika, preverjanje tipov
podatkovni tipi (seznami, terke, zapisi, opcije)
lokalno okolje, vezave, senčenje
sinonimi za podatkovne tipe
deklaracija lastnih alternativnih in rekurzivnih tipov
ujemanje vzorcev (tudi rekurzivno)
polimorfizem
izjeme
repna rekurzija, funkcijski sklad
funkcije višjega reda (kot argumenti ali rezultat funkcij), map/filter/fold
leksikalni doseg, funkcijske ovojnice, dinamični doseg
currying, delna aplikacija
statično/dinamično tipiziranje, implicitno/eksplicitno tipiziranje
mutacija
določanje podatkovnih tipov, omejitev vrednosti
vzajemna
moduli (organizacija in skrivanje programske kode)

Pregled

uvod v Racket
dinamično tipiziranje
lokalno okolje
zakasnjena evalvacija
- zakasnitvena funkcija
- zakasnitev in sprožitev
- tokovi
memoizacija
makro sistem

1.4.1 Uvod v Racket

1.4.1.1 Racket

Literatura: The Racket Guide

Tudi funkcijski jezik:

vse je izraz, ovojnice, anonimne funkcije, currying
je dinamično tipiziran: uspešno prevede več programov, vendar se večina napak zgodi šele pri izvajanju

Primeren za učenje novih konceptov:

zakasnjena evalvacija
tokovi
makri
memoizacija

Naslednik jezika Scheme.

Razvojno okolje: DrRacket

koda in REPL

1.4.1.2 Oklepaji

veliko jih je ☺
primerjava z značkami v sintaksi HTML
imajo poseben pomen: niso namenjeni samo prioriteti izračunov
uporabljamo lahko tudi [] namesto (),
morajo biti v pravih parih

Različni pomeni izrazov v odvisnosti od oklepajev:

e     ; izraz
(e)   ; klic funkcije e, ki prejme 0 argumentov
((e)) ; klic rezultata funkcije e, ki prejme 0 argumentov

(define (potenca x n)
   (if (= n 0)
      |1|bg:red|
      (* x (potenca x (- n 1)))))

≠

(define (potenca x n)
   (if (= n 0)
      |(1)|bg:red|
      (* x (potenca x (- n 1)))))

Omogočajo nedvoumno sintakso (opredeljujejo prioriteto operatorjev) in predstavitev v drevesni obliki (razčlenjevanje):

(define pristej1
   (lambda (x)
      (+ x 1)))

⬌

1.4.1.3 Osnove

; To je komentar

#|
To je večvrstični komentar
|#

modul je zbirka deklaracij
#lang racket na vrhu datoteke

#lang racket ; prva direktiva na vrhu datoteke

deklaracija:

(define x "Hello world")

; definicija spremenljivke
(define x "Hello world")   

; operacije
(define q 3)
(define w (+ q 2))
(define e (+ q 2 1 w))

deklaracija funkcije z besedo lambda (ali sintaktična olepšava):

(define sestej1
   (lambda (a b)
      (+ a b)))

⬌

; (sintaktična olepšava)
(define (sestej2 a b)
   (+ a b))

stavek if:

(if pogoj ce_res ce_nires)

;POGOJNI STAVEK (IF)
> (if (< 3 2) "a" 100)
100
> (if (< 3 12) "a" #t)
"a"

currying:

(define potenca2
   (lambda (x)
      (lambda (n)
         (potenca x n))))

; CURRYING
; izračun potence
(define (pot x n)
   (if (= n 0) 
      1
      (* x (pot x (- n 1)))))

; ovojna funkcija, ki izvaja currying argumentov
(define potenca2
  (lambda (x)
      (lambda (n)
         (pot x n))))

; oklepaji se uporabljajo za klicanje funkcije
> (potenca2 2)
> ((potenca2 2) 3) 

(define stiri_na (potenca2 4))
> (stiri_na 3)

Izrazi:

atomi (konstante in imena spremenljivk): 3.14, 5, #t, #f, x, y
rezervirane besede: lambda, if, define
zaporedja izrazov v oklepajih (e1 e2 ... en)
- e1 je lahko rezervirana beseda ali ime funkcije

Logične vrednosti:

#t in #f
vse vrednosti, ki niso #f, se obravnavajo kot #t (to v statično tipiziranih jezikih ni možno!)

> (if "lala" "DA" "NE")
"DA"
> (if null "DA" "NE")
"DA"
> (if "" "DA" "NE")
"DA"
> (if 0 "DA" "NE")
"DA"
> (if #f "DA" "NE")
"NE"

1.4.1.4 Seznami in pari

Seznami in pari se tvorijo z istim konstruktorjem (cons) ← prednost dinamično tipiziranega jezika (ne potrebujemo ločenih konstruktorjev, ki že pri prevajanju nakazujejo na pravilni tip podatka):

cons  ; konstruktor
null  ; prazen "element" (seznam)
null? ; ali je seznam prazen?
car   ; glava
cdr   ; rep
; funkcija za tvorjenje seznama
(list e1 e2 ... en)

Konstruktor cons oblikuje par (lahko je gnezden – potem par postane terka). Seznam je samo posebna oblika para/terke, ki ima na najbolj vgnezdenem mestu null:

> (cons "a" 1)
'("a" . 1)           ; par
> (cons "a" (cons 2 (cons #f 3.14)))
'("a" 2 #f . 3.14)   ; terka
> (cons "a" (cons 2 (cons #f (cons 3.14 null))))
'("a" 2 #f 3.14)     ; seznam
> (list "a" 2 #f 3.14)
'("a" 2 #f 3.14)     ; enak seznam (lepše)

Razpoznavanje seznama (angl. proper list) in parov (angl. pair):

(list? e)   ; vrne #t, če je e seznam
(pair? e)   ; vrne #t, če je e seznam ali par (karkoli narejenega s cons)

Kdaj uporabiti par in kdaj seznam?

podobno razmišljanje kot pri terkah/seznamih
par: hiter zapis števila elementov fiksnega tipa
seznam: zapis večjega števila elementov nedorečene velikosti

Dostop do elementov seznama:

(define p1 (cons "a" 1))
(define p2 (cons "a" (cons 2 (cons #f 3.14))))
(define l1 (cons "a" (cons 2 (cons #f null))))
(define l2 (cons "a" (cons 2 (cons #f (cons 3.14 null)))))
(define sez (list "a" 2 #f 3.14))

> (car sez)
"a"
> (cdr sez)
'(2 #f 3.14)
> (car (cdr (cdr sez)))
#f
> (car (cdr (cdr (cdr l2))))
3.14
> (null? (cdr (cdr (cdr (cdr l2)))))
#t

Primeri

Napiši funkcije za delo s seznami:

seštej elemente v seznamu
preštej elemente v seznamu
združi seznam
odstrani prvo pojavitev elementa v seznamu
odstrani vse pojavitve elementa v seznamu
vrni n-ti elementi
vrni vse elemente razen n-tega
map
filter
foldl (reduce)

; ******************** FUNKCIJE NAD SEZNAMI *********************

; 1. vsota seznama
(define (vsota_sez sez)
  (if (null? sez)
      0
      (+ (car sez) (vsota_sez (cdr sez)))))

; filter
(define (mojfilter f sez)
  (if (null? sez)
      null
      (if (f (car sez))
          (cons (car sez) (mojfilter f (cdr sez)))
          (mojfilter f (cdr sez)))))

; vgnezdeno štetje
(define a (list 1 2 5 "a"))
(define b (list (list 1 2 (list #f) "lala") (list 1 2 3) 5))

; vgnezdeno štetje - s stavkom IF
(define (prestej sez)
  (if (null? sez)
      0
      (if (list? (car sez))
          (+ (prestej (car sez)) (prestej (cdr sez)))
          (+ 1 (prestej (cdr sez))))))

; vgnezdeno štetje - s stavkom COND
(define (prestej1 sez)
  (cond [(null? sez) 0]
        [(list? (car sez)) (+ (prestej (car sez)) (prestej (cdr sez)))]
        [#t (+ 1 (prestej (cdr sez)))]))

1.4.2 Dinamično tipiziranje

Racket pri prevajanju ne preverja podatkovnih tipov:

slabost: uspešno lahko prevede programe, pri katerih nato pride do napake pri izvajanju (če programska logika pripelje do dela kode, kjer se napaka nahaja)
prednost: naredimo lahko bolj fleksibilne programe, ki niso odvisni od pravil sistema za statično tipiziranje
- fleksibilne strukture brez deklaracije podatkovnih tipov (npr. seznami in pari)
- primer spodaj:

(define (prestej sez)
   (if (null? sez)
      0
      (if (list? (car sez))
         (+ (prestej (car sez)) (prestej (cdr sez)))
         (+ 1 (prestej (cdr sez))))))

> (prestej (list (list 1 2 (list #f) "lala") (list 1 2 3) 5))
8

1.4.3 Pogojni stavek `cond`

Boljši stil namesto vgnezdenih if stavkov:

(cond [pogoj1 e1]
      [pogoj2 e2]
      ...
      [pogojN eN])

Semantika: če velja pogoj1, evalviraj izraz e1 itd.

Oglati oklepaji so le konvencija, niso obvezni (lahko so okrogli).

Smiselno je, da je pogojN = #t (“globalni” else):

(define (prestej1 sez)
   (cond [(null? sez) 0]
         [(list? (car sez)) (+ (prestej1 (car sez)) (prestej1 (cdr sez)))]
         [#t (+ 1 (prestej1 (cdr sez)))]))

1.4.4 Lokalno okolje

Različne vrste definiranj lokalnega okolja za različne potrebe:

let      ; izrazi se evalvirajo v okolju PRED izrazom let
let*     ; izrazi se evalvirajo kot rezultat predhodnih deklaracij (tako dela SML)
letrec   ; izrazi se evalvirajo v okolju, ki vključuje vse podane deklaracije (vzajemna rekurzija)
define   ; semantika ekvivalentna kot pri letrec, le drugačna sintaksa

Pozor: sintaksa (let ([..]…[..]) (telo)):

(define (test-let a|arrow_end|)
   (|let|bg:red| ([a 3]
            [b (+ a|arrow_start| 2)])
      (+ a b)))

> (test-let 10)
15

; 3 + (10+2) = 15

(define (test-let* a)
   (|let*|bg:red||arrow_end|    ([a 3]
            [b (+ a|arrow_start| 2)])
      (+ a b)))

> (test-let* 10)
8

; 3 + (3+2) = 8

letrec in define: podobno kot vzajemna rekurzija v SML (operator and).

Pozor: izrazi se vedno evalvirajo v vrstnem redu, takrat morajo biti spremenljivke definirane; izjema so funkcije: telo se izvede šele ob klicu funkcije.

(Globalne) deklaracije v programski datoteki se obnašajo kot letrec:

(define (test-letrec a)
   (letrec ([b 3]
            [c (lambda (x) (+ a b d x))]
            [d (+ a 1)])
   (c a)))

> (test-letrec 50)
154                  |check|

; 154   ; a=50, b=3, c=..., d= 51
; (c 50) = 50 + 3 + 51 + 50 = 154

⬍

enakovredno

(define (test-define a)
   (define b 3)
   (define c (lambda (x) (+ a b d x)))
   (define d (+ a 1))
   (c a))

(define (test-letrec2 a)
   (letrec ([b 3]
      [c (+ d|arrow_end| 1)]
      [d (+ a 1)])
   (+ a d)))   |arrow_start|

> (test-letrec2 50) |warning|
; d: undefined;
; cannot use before initialization

Nedelovanje: deklaracije se izvajajo zaporedno!

1.4.5 Zakasnjena evalvacija

1.4.5.1 Zakasnitvena funkcija

1.4.5.1.1 Takojšnja in zakasnjena evalvacija

Semantika programskega jezika mora opredeljevati, kdaj se izrazi evalvirajo.

Spomnimo se primera deklaracij (define x e):

če je e aritmetični izraz, se ta evalvira takoj ob vezavi, v x se shrani rezultat (takojšnja ali zgodnja evalvacija, angl. eager evaluation)
če je e funkcija, torej (lambda …), se telo evalvira šele ob klicu (x)(zakasnjena evalvacija, angl. delayed evaluation)

Kako je s pogojnim stavkom (if pogoj res nires)? Izraza res in nires se evalvirata šele po evalvaciji pogoj-a in vedno samo eden.

; sintaksa:
; (if pogoj res nires)

(define (potenca x n)|check|
   (if (= n 0)
      1
      (* x (potenca x (- n 1)))))

(define (moj-if pogoj res nires)
   (if pogoj res nires))
   
(define (potenca-moj x n)|warning|
   (moj-if (= n 0)
      1
      (* x (potenca-moj x (- n 1)))))

Primer, ki ne deluje - neskončna rekurzija.

Zakaj desni primer ne deluje?

moj-if je funkcija, zato Racket najprej ovrednoti vse argumente (tudi rekurzivni klic potenca-moj), preden preveri pogoj → neskončna rekurzija.

Ideja:

če želimo zakasniti evalvacijo, zapišemo izraz v funkcijo (lahko brez parametrov)
- (lambda () e)
kadar želimo izvesti evalvacijo izraza, funkcijo pokličemo

Angl. thunking.

thunk functional programming

web definitions

In computer science, a thunk is parameterless closure created to prevent evaluation of an expression until forced of a later time.

(define (moj-if-super pogoj res nires)
   (if pogoj |(res)|bg:purple| |(nires)|bg:red|))

(define (potenca-super x n)
   (moj-if-super (= n 0)
      |(lambda () 1)|bg:purple|
      |(lambda () (* x (potenca-super x (- n 1)))|bg:red|)))

1.4.5.1.2 Zakasnjena evalvacija

Za zakasnitev evalvacije, kodo ovijemo v funkcijo brez parametrov (angl. thunk); evalvacija se izvede ob klicu funkcije, koristno je vedeti, kolikokrat se bo izraz evalviral:

; izraz znotraj x se evalvira 0 krat
(define (fun1 x)
   (if #t "zivjo" (x)))

; izraz se evalvira 1 krat
(define (fun2 x)
   (if #f "zivjo" (x)))

; izraz se evalvira 1 krat|arrow_end|
(define (fun4 x)
   (let* ([t (x)])            |arrow_start|
   (begin               |kaj pa, če to|color:cornflowerblue|
      (if pogoj1 xxx t)   |sploh ni|color:cornflowerblue|
      (if pogoj2 xxx t)   |potrebno?|color:cornflowerblue|
         ...
      (if pogoj xxx t))))

; izraz se evalvira 0 do n|arrow_end| krat
(define (fun3 x)
   (begin                      |arrow_start|
      (if pogoj1 xxx (x))   |ponavljanje|color:cornflowerblue|
      (if pogoj2 xxx (x))      |iste|color:cornflowerblue|
      (if pogoj3 xxx (x))    |evalvacije|color:cornflowerblue|
         ...
      (if pogojn xxx (x))))

Ideja: izvedimo leno evalvacijo – naredimo mehanizem, ki evalvira izraz takrat, ko ga prvič potrebujemo. Pri nadaljnjih klicih vrnemo že evalvirano vrednost (izraz torej evalviramo največ enkrat – in sicer le v primeru potrebe po vrednosti).

Na predavanjih:

; funkcija za testiranje - vrne število x z zakasnitvijo (simulacija dolgega izračuna)
(define (dolga_operacija x)
  (begin
    (printf "Dolga operacija~n")
    (sleep 1)    ; počaka 1 sekundo
    x))


; ***************************************************************
; 1. PRIMER: osnovna verzija potence, eksponent zakasnjen *******

; izračuna x^n; n dobimo zakasnjeno (thunk) s klicem (klic_n)
(define (potenca x klic_n)
  (cond [(= x 0) 0]
        [(= x 1) 1]
        [(= (klic_n) 1) x]
        [#t (* x (potenca x (lambda () (- (klic_n) 1))))]))

(potenca 0   (lambda () (dolga_operacija 2)))    ; 0x evalvacija eksponenta  :)
(potenca 1   (lambda () (dolga_operacija 20))    ; 0x evalvacija eksponenta  :)
(potenca 200 (lambda () (dolga_operacija 1)))    ; 1x evalvacija eksponenta  :|
(potenca 2   (lambda () (dolga_operacija 4)))    ; 4x evalvacija eksponenta  :(


; ***************************************************************
; 2. PRIMER: uporabimo lokalno spremenljivko za eksponent *******

(potenca 0   (let ([rez (dolga_operacija 2)]) (lambda () rez)))   ; 1x evalvacija eksponenta  :(
(potenca 1   (let ([rez (dolga_operacija 2)]) (lambda () rez)))   ; 1x evalvacija eksponenta  :(
(potenca 200 (let ([rez (dolga_operacija 1)]) (lambda () rez)))   ; 1x evalvacija eksponenta  :|
(potenca 2   (let ([rez (dolga_operacija 4)]) (lambda () rez)))   ; 1x evalvacija eksponenta  :)

1.4.5.2 Zakasnitev in sprožitev

1.4.5.2.1 Potrebovali bomo…

Zaporedje izrazov:

zaporedje vrne vrednost zadnjega izraza v zaporedju

(begin e1 e2 ... en)

Par, katerega komponente lahko spreminjamo:

cons ne podpira mutacije
novi konstruktor mcons (mutable cons)

mcons       ; konstruktor
mcar        ; glava
mcdr        ; rep
mpair?      ; je par?
set-mcar!   ; nastavi novo glavo
set-mcdr!   ; nastavi novi rep

funkcij za navadne pare (cons) ne moremo uporabljati na mcons

1.4.5.2.2 Zakasnitev in sprožitev

Zakasnitev (angl. delay), sprožitev (angl. force).

Mehanizem je že vgrajen v Racket (mi ga sprogramiramo sami).

Delay prejme zakasnitveno funkcijo in vrne par s komponentama:

bool: indikator, ali je izraz že evalviran
zakasnitvena funkcija ali evalviran izraz

; ZAKASNITEV
(define (my-delay thunk)
   (mcons #f thunk))

; SPROŽITEV
(define (my-force prom)
   (if (mcar prom)
      (mcdr prom)
      (begin (set-mcar! prom #t)
            (set-mcdr! prom ((mcdr prom)))
            (mcdr prom))))

> (define md
     (my-delay
        (lambda () (+ 3 2))))

> md
(mcons #f #<procedure>)

> (my-force md)
5

> md
(mcons #t 5)

; ***************************************************************
; 3. PRIMER: uporabimo zakasnitev in sprožitev ******************

; ORODJE: delo s spremenljivimi seznami (MCONS)
(define msez (mcons 1 (mcons 2 3)))
msez
(mcar msez)
(mcdr msez)
(mcar (mcdr msez))
(set-mcar! msez 4)
msez
(set-mcdr! msez (mcons 5 6))
(set-mcar! (mcdr msez) 7)


; zakasnitev
(define (my-delay thunk) 
  (mcons #f thunk)) 

; sprožitev
(define (my-force prom)
  (if (mcar prom)
      (mcdr prom)
      (begin (set-mcar! prom #t)
             (set-mcdr! prom ((mcdr prom)))
             (mcdr prom))))

; primer delovanja zakasnitve in sprožitve  
> (define md (my-delay (lambda () (+ 3 2))))
> md
> (mcdr md)
> ((mcdr md))
> (my-force md)
> md
> (my-force md)
> (my-force md)
> md


(potenca 0 (let* ([rez (my-delay (lambda () (dolga_operacija 2)))]) 
             (lambda () (my-force rez))))                            ; 0x evalvacija eksponenta  :)
(potenca 1 (let* ([rez (my-delay (lambda () (dolga_operacija 2)))]) 
             (lambda () (my-force rez))))                            ; 0x evalvacija eksponenta  :)
(potenca 200 (let* ([rez (my-delay (lambda () (dolga_operacija 1)))]) 
               (lambda () (my-force rez))))                          ; 1x evalvacija eksponenta  :|
(potenca 200 (let* ([rez (my-delay (lambda () (dolga_operacija 3)))]) 
               (lambda () (my-force rez))))                          ; 1x evalvacija eksponenta  :)

1.4.5.3 Tokovi

Tok: neskončno zaporedje vrednosti (npr. naravna števila), ki ga ne moremo definirati s podajanjem vseh vrednosti.

Ideja: podajmo le (trenutno) vrednost in zakasnimo evalvacijo (thunk) za izračun naslednje vrednosti.

Definirajmo tok kot par:

'(vrednost . funkcija-za-naslednji)

V paru:

zakasnjena funkcija (thunk) generira naslednji element v zaporedju, ki je tudi par enake oblike,
zakasnjena funkcija lahko vsebuje tudi rekurzivni klic, ki se izvede šele ob klicu funkcije

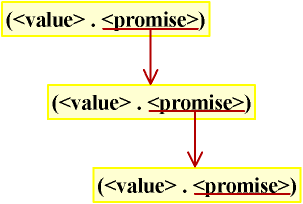
dostop do elementov:

(car s)                 ; prvi element
(car ((cdr s)))         ; drugi element
(car ((cdr ((cdr s))))) ; tretji element

Primeri

Definiraj naslednje tokove:

zaporedje samih enic
zaporedje naravnih števil
zaporedje 1, -1, 1, -1, …
zaporedje potenc števila 2

Zapiši funkcije za delo s tokovi:

izpiši prvih n števil v toku
izpisuj tok, dokler velja pogoj
izpiši, koliko števil je v toku, preden velja pogoj

(define enke (cons 1 (lambda () enke)))

(car enke)                    ; prvi element
(car ((cdr enke)))            ; drugi element
(car ((cdr ((cdr enke)))))    ; tretji element


(define naravna
   (letrec ([f (lambda (x)
      (cons x (lambda () (f (+ x 1)))))])
                  (f 1)))

(define plusminus
   (letrec ([f (lambda (x)
      (cons x (lambda () (if (= x 1) (f -1) (f 1)))))])
                  (f 1)))

(define potence
   (letrec ([f (lambda (x)
      (cons x (lambda () (f (* x 2)))))])
                  (f 2)))

; funkcije nad tokovi

; izpiši prvih n
(define (izpisi n tok)
  (if (> n 1) 
      (begin
        (displayln (car tok))
        (izpisi (- n 1) ((cdr tok))))
      (displayln (car tok))))

; izpisi dokler velja POGOJ
(define (izppog tok pogoj)
  (cond [(pogoj (car tok)) (begin
                             (displayln (car tok))
                             (izppog ((cdr tok)) pogoj))]
        [#t #t]))

1.4.6 Memoizacija

Če funkcija pri istih argumentih vsakič vrača isti odgovor (in nima stranskih učinkov), lahko shranimo odgovore za večkratno rabo.

Smotrnost?

ali je shranjevanje hitrejše od ponovnega računanja?
ali bodo shranjeni rezultati kdaj uporabljeni?

Primer: Fibonaccijeva števila, poenostavitev eksponentne časovne zahtevnosti?

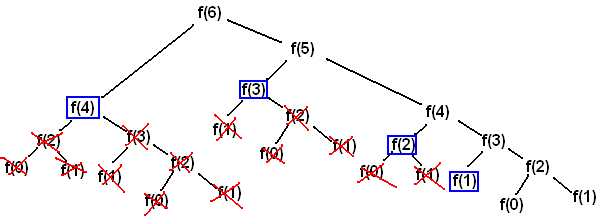
Implementacija:

uporabimo seznam parov dosedanjih rešitev '((arg1, odg1), ..., (argn, odgn))
- ne želimo, da je globalno dostopen
- ne sme biti v rekurzivni funkciji, ker bo spraznil z vsakim klicem
če rešitev obstaja, jo beremo iz seznama
- pomagamo si lahko z vgrajeno funkcijo assoc
če rešitve še ni, jo izračunamo → dopolnimo seznam rešitev
- za dopolnitev seznama potrebujemo mutacijo (set!)

(define fib3
   (letrec ([resitve null]
            [pomozna (lambda (x)
                     (let ([ans (assoc x resitve)])         ; poiscemo resitev
                     |(if ans       |bg:green|
                     |     (cdr ans)|bg:green|                        ; vrnemo obstojeco resitev
                           (let ([nova (cond [(= x 1) 1]    ; resitve ni
                                             [(= x 2) 1]
                                             [#t (+ (pomozna (- x 1))      ; izracun resitve
                                                   (pomozna (- x 2)))])])
                           |(begin                                          |bg:red|
                           |   (set! resitve (cons (cons x nova) resitve))  |bg:red|; shranimo resitev
                           |   nova)))))])                                  |bg:red|; vrnemo resitev
   pomozna))

Na predavanjih:

; rekurzivna rešitev
(define (fib1 x)
  (cond [(= x 1) 1]
        [(= x 2) 1]
        [#t (+ (fib1 (- x 1))
               (fib1 (- x 2)))]))

; rekurzivna rešitev z akumulatorjem
(define (fib2 x)
  (letrec ([pomozna (lambda (f1 f2 n)   ; n-to fib število se izračuna kot f1 + f2
                      (cond [(= n x) (+ f1 f2)]
                            [#t (pomozna f2 (+ f1 f2) (+ n 1))]))])
    (cond [(= x 1) 1]
          [(= x 2) 1]
          [#t (pomozna 1 1 3)])))      


; assoc
; (define resitve (list (cons 1 "a") (cons 2 "b") (cons 3 "c") (cons 4 "d")))
; (assoc 2 resitve)
; (assoc 4 resitve)
; (assoc 7 resitve)
; (assoc "b" resitve)


;(set! spremenljivka vrednost) ; spremeni vrednost x
;(define x 15)
;(set! x 9)                    ; mutacija

;(define resitve (list (cons 1 "a") (cons 2 "b") (cons 3 "c") (cons 4 "d")))
;(set! resitve 4)              ; spremeni podatkovni tip

;(car (car resitve))

;(set! (car (car resitve)) 5)  ; ne moremo spreminjati delov seznama

;(define resitve null)

1.4.7 Makro sistem

Makro definira, kako sintakso v programskem jeziku preslikamo v drugo sintakso:

orodje, ki ga ponuja programski jezik
razširitev jezika z novimi ključnimi besedami
implementacija sintaktičnih olepšav

Programski jeziki (Racket, C, …) imajo posebno sintakso za definiranje makrov.

Postopek razširitve makro definicij (angl. macro expansion) se izvede pred prevajanjem in izvajanjem programa.

Primeri:

lasten stavek if: (moj-if pogoj then e1 else e2)
trojni if: (if3 pog then e1 elsif pogoj2 then e2 else e3)
elementi toka: (prvi tok), (drugi tok), (tretji tok)
komentiranje spremenljivk: (anotiraj xyz "trenutni stevec")

1.4.7.1 Definicija makrov

Rezervirana beseda define-syntax.

Preostale ključne besede opredelimo s syntax-rules.

V [ ... ] podamo vzorce za makro razširitev.

Primeri:

(define-syntax if-trojni
   (syntax-rules (then elsif else)
   [(if-trojni e1 then e2 elsif e3 then e4 else e5)
      (if e1 e2 (if e3 e4 e5))]))

(define-syntax tretji
   (syntax-rules ()
      [(tretji e)
         (car ((cdr ((cdr e)))))]))

(define-syntax anotiraj
   (syntax-rules ()
      [(anotiraj e s)
         e]))

; PRIMERI MAKROV ***********************************************


; moj-if, ki uporablja besedi then in else
(define-syntax mojif             ; ime makra
  (syntax-rules (then else)       ; druge ključne besede
    [(mojif e1 then e2 else e3)  ; sintaksa makra
     (if e1 e2 e3)]))             ; razširitev makra

; trojni if z 2 pogojema in 3 izidi
(define-syntax if-trojni 
  (syntax-rules (then elsif else)
    [(if-trojni e1 then e2 elsif e3 then e4 else e5)
     (if e1 e2 (if e3 e4 e5))]))
; (if-trojni #t then 1 elsif #t then 2 else 3)
; (if-trojni #f then 1 elsif #t then 2 else 3)
; (if-trojni #f then 1 elsif #f then 2 else 3)

; prvi element toka
(define-syntax prvi 
  (syntax-rules ()
    [(prvi e)
     (car e)]))
; drugi element toka
(define-syntax drugi
  (syntax-rules ()
    [(drugi e)
     (car ((cdr e)))]))
; tretji element toka
(define-syntax tretji
  (syntax-rules ()
    [(drugi e)
     (car ((cdr ((cdr e)))))]))

;(define naravna
;  (letrec ([f (lambda (x) (cons x (lambda () (f (+ x 1)))))])
;    (f 1)))


; (prvi naravna)
; (drugi naravna)
; (tretji naravna)

;anotacija spremenljivk
(define-syntax anotiraj
  (syntax-rules ()
    [(anotiraj e s)
     e]))

; primer anotacije spremenljivk

(define fib4
  (letrec ([resitve (anotiraj null "zacetna resitev je prazna")]  
           [pomozna (lambda (x)
                      (let ([ans (assoc x resitve)])         
                        (if (anotiraj ans "odgovor ze obstaja") 
                            (anotiraj (cdr ans) "vrnemo obstojeco resitev")
                            (let ([nova (cond [(= x 1) 1]         ; resitve ni
                                              [(= x 2) 1]
                                              [#t (+ (pomozna (- x 1))      ; izracun resitve
                                                     (pomozna (- x 2)))])])
                              (begin 
                                (set! resitve (cons (cons x nova) resitve)) ; shranimo resitev
                                nova)))))])                                 ; vrnemo resitev
    pomozna))

Lastnosti:

definiramo lahko lastne rezervirane besede (then, elsif)
možne sintaktične napake:
- pri uporabi sintakse za makro
- pri uporabi sintakse, v katero se makro razširi

1.4.7.2 Lastnosti makrov

Makro zamenjuje ključne besede (sintaksne žetone) in ne posameznih črk (torej pravilo “or → uta” ne naredi zamenjave v izrazih “(+ c minor)” → “(+ c minuta)”).

Posebno pozornost je potrebno posvetiti:

ali je makro sploh potreben (morda zadošča funkcija)?
prioriteta izračunanih izrazov
način evalvacije izrazov v makrih
semantika dosega spremenljivk; uporabljamo dve okolji:
- okolje v definiciji makra,
- okolje, kjer se makro razširi v programsko kodo

1.4.7.2.1 1. Primernost uporabe/smotrnost uporabe

Primer: my-delay in my-force

Pri my-delay smo morali podati zakasnjeno funkcijo (thunk):

(my-delay (lambda () (+ 3 2)))

Denimo, da želimo ta zapis poenostaviti v zapis brez besede lambda ():

(my-delay (+ 3 2))

Brez makrov ne obstaja način, da ta zapis poenostavimo, saj se argumenti evalvirajo takoj ob klicu funkcije!

Rešitev: uporabimo makro

(define-syntax my-delaym
   (syntax-rules ()
      [(my-delaym e)
         (mcons #f (lambda() e))]))

my-force nima implementacijskih težav, primeren je v obliki funkcije

pravzaprav: makro ne bi deloval, kot želimo (o tem malo kasneje)! ☺

; primernost uporabe my-delay in my-force

; DEFINICIJA ZAKASNITVE IN SPROŽITVE
; zakasnitev 
(define (my-delay-fun thunk) 
  (mcons #f thunk)) 
; sprožitev
(define (my-force-fun prom)
  (if (mcar prom)
      (mcdr prom)
      (begin (set-mcar! prom #t)
             (set-mcdr! prom ((mcdr prom)))
             (mcdr prom))))

; uporaba makra
(define-syntax my-delaym
  (syntax-rules ()
    [(my-delaym e)
     (mcons #f (lambda() e))]))

(define md (my-delay (lambda () (+ 3 2))))
(define mdm (my-delaym (+ 3 2)))

> (my-force md)
> md
> (my-force mdm)
> mdm

1.4.7.2.2 2. Prioriteta izračunov

Primer makra v C++:

#define ADD(x,y) x+y

Ta makro opravi zamenjavo izraza:

ADD(1,2)*3 → 1+2*3

(rešitev je 7 in ne morda 9)

Za pravilno delovanje moramo makro definirati kot:

#define ADD(x,y) ((x)+(y))

Racket teh težav nima, ker uporabljamo prefiksno notacijo, ki jasno opredeljuje prioriteto operacij.

Primer:

Makro:

(sestej a b) → (+ a b)

Pravilno opravi raširitev izraza:

(* (sestej 1 2) 3) → (* (+ 1 2) 3)

1.4.7.2.3 3. Način evalvacije izrazov

Potrebno je posvetiti pozornost temu, kolikokrat se določen izraz evalvira.

Primer makrov, ki nista ekvivalentna:

(define-syntax dvakrat3
   (syntax-rules() [(dvakrat3 x)(+ x x)])) ; x se evalvira 2x

(define-syntax dvakrat4
   (syntax-rules()[(dvakrat4 x)(* 2 x)])) ; x se evalvira 1x

Večkratne evalvacije lahko preprečimo z uporabo lokalnih spremenljivk (stavek let):

(define-syntax dvakrat5
   (syntax-rules()
      [(dvakrat5 x)(let ([mojx x]) (+ mojx mojx))]))

; ekvivalentno
(define (dvakrat1 x) (+ x x)) ; dostopamo do x 2-krat, evalvira se le 1-krat
(define (dvakrat2 x) (* 2 x)) ; dostopamo do x 1-krat, evalvira se le 1-krat

; ni ekvivalentno
(define-syntax dvakrat3 
  (syntax-rules()
    [(dvakrat3 x)(+ x x)]))
(define-syntax dvakrat4 
  (syntax-rules()
    [(dvakrat4 x)(* 2 x)]))

; testiranje zgornjega s pomožno funkcijo
; samo izpiše in vrne vrednost
(define (vrni x)
  (begin
    (displayln x)
    x))

> (dvakrat3 (vrni 5))
5
5
10

> (dvakrat4 (vrni 3))
3
6

; rešitev: uporaba lokalnih spremenljivk
(define-syntax dvakrat5
  (syntax-rules()
    [(dvakrat5 x)(let ([mojx x]) (+ mojx mojx))]))

> (dvakrat5 (vrni 3))
3
6

1.4.7.2.4 4. Semantika dosega

Kaj se zgodi, če makro uporablja iste spremenljivke, ki nastopajo že v funkciji?

Naivna makro razširitev (uporabljata jo C/C++; je enakovredna find&replace) lahko povzroči nepričakovane rezultate.

Primer:

(define-syntax swap
   (syntax-rules ()
      ((swap x y)
         (let ([tmp x])
            (set! x y)
            (set! y tmp)))))

> (let ([tmp 5]
      [other 6])
   |(let ([tmp tmp])    |bg:gray|                 ;    naivna makro
   |   (set! tmp other) |bg:gray||arrow_end|      |arrow_start|           ;  razširitev klica
   |   (set! other tmp))|bg:gray|                 ;  (swap tmp other)
   (list tmp other))
'(5 6)

V sistemih z naivnimi razširitvami se to rešuje z uporabo redkih imen spremenljivk (čudna imena, samo velike črke).

Vendar pa makro definicije tudi uporabljajo leksikalni doseg (higiena makro sistema):

uporaba vrednosti spremenljivk v kontekstu, kjer je makro definiran
samodejno preimenovanje lokalnih spremenljivk

Naivna makro razširitev:

> (let [tmp 5]    |arrow_end|     |arrow_start|
      [other 6])
   (let ([tmp tmp])
      (set! tmp other)
      (set! other tmp))
   (list tmp other))
'(5 6)         |warning|

Racket:

> (let ([tmp 5]
      [other 6])
   (swap tmp other)
   (list tmp other))|arrow_end|     |arrow_start|
'(6 5)         |check|

; 1. primer: upoštevanje leksikalnega dosega
(define-syntax formula   ; prišteje 5
  (syntax-rules ()
    [(formula x)
     (let ([y 5])
       (+ x y))]))

; naivna razširitev
(define (f1 x y)
  (+ x y (let ([y 5])
           (+ y y))))
> (f1 1 2)
13

; upoštevanje leksikalnega dosega
(define (f2 x y)
  (+ x y (formula y)))

> (f2 1 2)
10


; 2. primer: zamenjava elementov
(define-syntax swap
  (syntax-rules ()
    ((swap x y)
     (let ([tmp x])
       (set! x y)
       (set! y tmp)))))

; naivna razširitev
(let ([tmp 5]
      [other 6])
  (let ([tmp tmp])
    (set! tmp other)
    (set! other tmp))
  (list tmp other))

- '(5, 6)

; upoštevanje leksikalnega dosega
(let ([tmp 5]
      [other 6])
  (swap tmp other)
  (list tmp other))

- '(6, 5)

1.5 Lastni podatkovni tipi, interpreter, argumenti funkcij, primerjava FP in OUP

1.5.1 Lastni podatkovni tipi

V ML smo definirali lastne podatkovne tipe.

Spomnimo se, da datatype v ML ponuja:

alternative podvrst tipa:

(datatype x = PRVO | DRUGO | TRETJE)

rekurzivno definicijo tipa:

(datatype x = PRVO of x | DRUGO)

Racket:

dinamično tipiziran, zato eksplicitna definicija alternativ ni potrebna
preprosta rešitev:
- simulacija alternativ s seznami oblike
```
(tip vrednost1 ... vrednostn)
```
- izdelava funkcij za preverjanje podatkovnega tipa in funkcij za dostop do elementov
  
  Primer:

; ***************************************************************
; siulacija s seznami (tip vrednost1 ... vrednostn) *************


; datatype prevozno_sredstvo = Bus of int
;                             | Avto  of string * string 
;                             | Pes

; konstruktorji
(define (Bus n) (list "bus" n))
(define (Avto tip barva) (list "avto" tip barva))
(define (Pes) (list "pes"))
(define (Segment cas sredstvo) (list "segment" cas sredstvo))
; testiranje podatkovnega tipa
(define (Bus? x) (eq? (car x) "bus"))
(define (Avto? x) (eq? (car x) "avto"))
(define (Pes? x) (eq? (car x) "pes"))
(define (Segment? x) (eq? (car x) "segment"))
; dostop do elementov
(define (Bus-n x) (car (cdr x)))
(define (Avto-tip e) (car (cdr e)))
(define (Avto-barva e) (car (cdr (cdr e))))
(define (Segment-cas e) (car (cdr e)))
(define (Segment-sredstvo e) (car (cdr (cdr e))))

; primer programa nad lastnim podatkovnim tipom
; avtobus: 40 km/h; avto: 80 km/h; pes: 5 km/h
(define pot (list (Segment 2 (Avto "fiat" "modri")) (Segment 1 (Bus 22))))

(define (prevozeno pot)  ; izračuna, koliko kilometrov smo prevozili
  (if (null? pot) 0
      (let ([prvi (car pot)])
        (+ (cond [(Bus? (Segment-sredstvo prvi))  (* 40 (Segment-cas prvi))]
                 [(Avto? (Segment-sredstvo prvi)) (* 80 (Segment-cas prvi))]
                 [(Pes? (Segment-sredstvo prvi))  (* 5 (Segment-cas prvi))]
                 [#t (error "Napačno prevozno sredstvo")])
           (prevozeno (cdr pot))))))

1.5.1.1 Nerodnost…

Rešitev ni praktična, dopušča veliko možnosti za napake:

pri konstruktorju podamo napačno vrednost

(Segment "kuku" (Avto "fiat" "modri"))
(define pot (list (Segment "kuku" (Avto "fiat" "modri")) (Segment 1 (Bus 22))))

preverjanje tipa povzroči napako, če ne upoštevamo načina implementacije
```
(define (Avto? x) (eq? (car x) "avto"))
(Avto? "zivjo")
```

dostop do elementov ne preveri, ali je vsebina pravega tipa

(define (Avto-barva e) (car (cdr (cdr e))))
(Avto-barva (Avto 3.14 2.71))
(Avto-tip (Bus 4))

sami izdelujemo lastne sezname brez uporabe konstruktorjev
```
(define x (list "avto" "porsche" "rdec"))
```
uporaba lastnih metod za dostop (obremenjevanje z implementacijo)
```
namesto (Avto-barva x) uporabimo (car (cdr x))
```

Breme izogibanja napakam pade na program in pomožne funkcije.

1.5.1.2 Boljši način: struct

Definicija lastnega tipa s komponentami

(struct ime (komp1 komp2 ... kompn) #:transparent|arrow_end|)

                                             |arrow_start|
                                    |atribut, ki omogoča|color:cornflowerblue|
                                       |izpis v REPL|color:cornflowerblue|

Rezultat je avtomatska izdelava funkcij:

(ime komp1 komp2 ... kompn) konstruktor novega tipa
(ime? e) preverjanje vrste tipa
(ime-komp1 e), ..., (ime-kompn e) dostop do komponent (ali napaka)

Prednosti:

implementacija tipa je popolnoma skrita
razširitev programa z novim podatkovnim tipom
samodejno preverjanje napak
podatka ne moremo izdelati drugače kot s konstruktorjem
do podatka ne moremo dostopati drugače kot s funkcijami za dostop
primeri:

; ***************************************************************
; simulacija z vgrajenim mehanizmom: struct *********************

(struct bus (n) #:transparent)
(struct avto (tip barva) #:transparent)
(struct pes () #:transparent)
(struct segment (cas sredstvo) #:transparent)

(define pot1 (list (segment 2 (avto "fiat" "modri")) (segment 1 (bus 22))))

(define (prevozeno1 pot)
  (if (null? pot) 0
      (let ([prvi (car pot)])
        (+ (cond [(bus? (segment-sredstvo prvi)) (* 40 (segment-cas prvi))]
                 [(avto? (segment-sredstvo prvi)) (* 80 (segment-cas prvi))]
                 [(pes? (segment-sredstvo prvi)) (* 5 (segment-cas prvi))]
                 [#t (error "Napačno prevozno sredstvo")])
           (prevozeno1 (cdr pot))))))

1.5.2 Interpreter

1.5.2.1 Definicija konstruktov

1.5.2.1.1 Interpreter ali prevajalnik?

Dve alternativi za implementacijo programskega jezika:

INTERPRETER za programski jezik X
- napišemo ga v programskem jeziku 0
- program je v sintaksi jezika X
- odgovor je v sintaksi jezika X
PREVAJALNIK za programski jezik X
- napišemo ga v programskem jeziku 0
- program je v sintaksi jezika X
- rezultat je program v jeziku P
- program v jeziku X in program v jeziku P imata ekvivalenten pomen

Narediti interpreter ali prevajalnik je le predmet implementacije, ne definicije programskega jezika.

Možne so tudi kombinacije prevajanja in interpretiranja:

Java je prevajalnik v JVM
delno prevajanje (optimizacija) in delno interpretiranje programa

1.5.2.1.2 Izvajanje programa

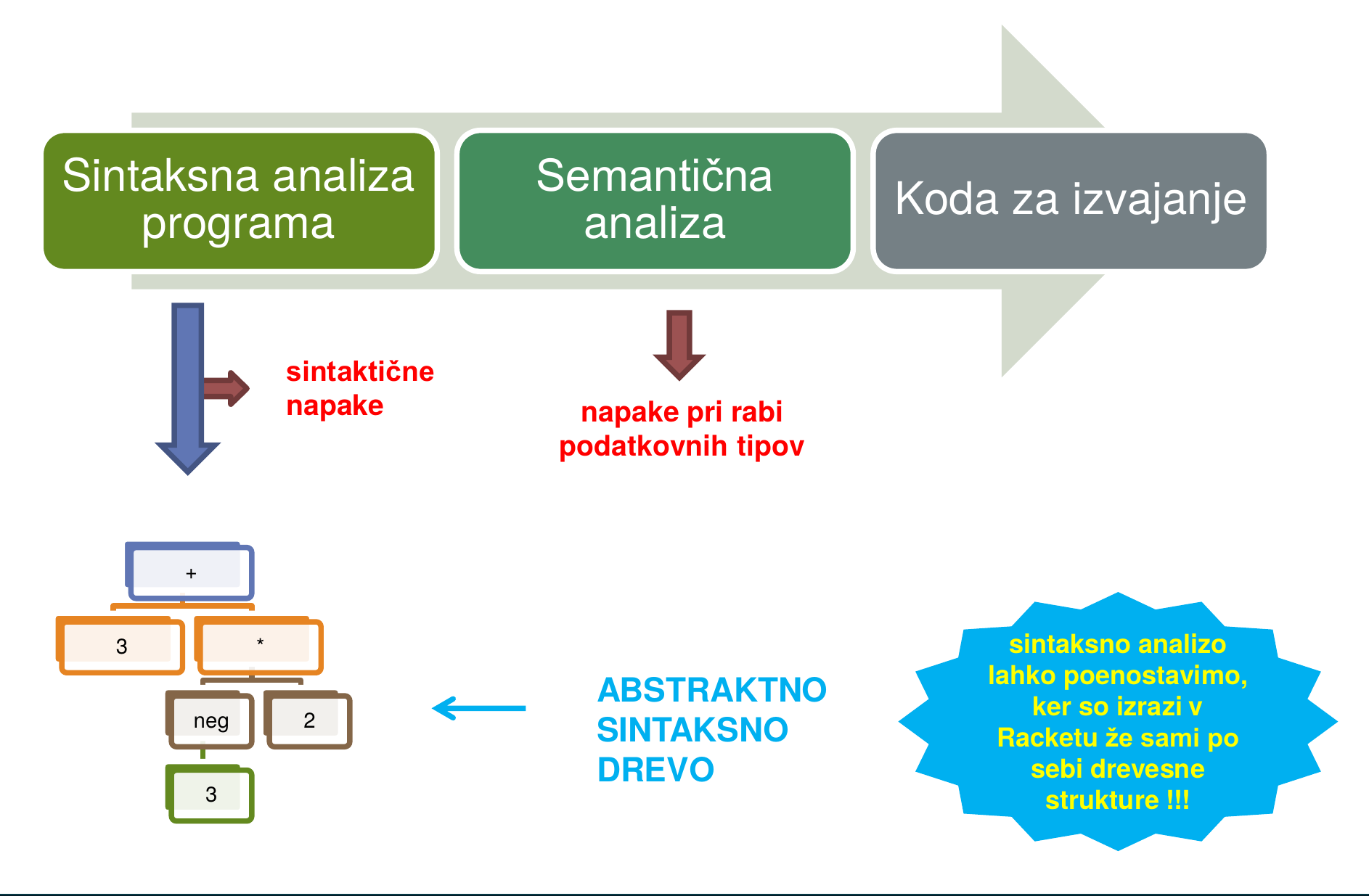
1.5.2.1.3 Naš pristop

Preskočimo fazo sintaksne analize in razčlenjevanja s podajanjem AST, ki je že v izvornem programskem jeziku 0.

Sintakso ciljnega jezika X lahko definiramo z uporabo lastnih podatkovnih tipov (struct).

Primer: JAIS (Jezik Aritmetičnih Izračunov v Slovenščini)

rekurzivna funkcija za računanje z izrazi
izrazi za:
- definicijo konstant (konst)
- definicijo logičnih vrednosti (bool)
- negacijo (negiraj)
- seštevanje (sestej)
- vejanje (ce-potem-sicer)

1.5.2.1.4 Preverjanje pravilnosti programa

Primer interpreterja za JAIS:

(define (jais e)
   (cond [(konst? e) e]      ; vrnemo izraz v ciljnem jeziku
         [(bool? e) e]             |preverjanje ustreznosti podatkovnih tipov|color:cornflowerblue|
         [(negiraj? e)                    |(semantika) že izvajamo|color:cornflowerblue|
         (let ([v (jais (negiraj-e e))])           |arrow_start|
            (cond 
               [|(konst? v)|color:cornflowerblue| (konst-int v)]
               [|(bool? v)|color:cornflowerblue| (not (bool-b v))]
               [#t (error "negacija nepričakovanega izraza")]))]
         
         [(sestej? e)
         (let ([v1 (jais (sestej-e1 e))]
               [v2 (jais (sestej-e2 e))])    |arrow_end|
            (if (and |(konst? v1)|color:cornflowerblue| |(konst? v2)|color:cornflowerblue|)
               (konst (+ (konst-int v1) (konst-int v2)))
               (error "seštevanec ni številka")))]
         [#t (error "sintaksa izraza ni pravilna")]))

Preverjanje ustreznosti podatkovnih tipov.

Preverjanje pravilne sintakse?

delno preverja že Racket (jais (negiraj 1 2 3))
napaka: (jais (negiraj (konst "lalala")))
potrebno dopolniti kodo, da preverja tudi pravilno sintakso konstant!

(struct konst (int) #:transparent)     ; konstanta; argument je število
(struct bool (b) #:transparent)        ; b ima lahko vrednost true or false
(struct negiraj (e) #:transparent)     ; e je lahko izraz
(struct sestej (e1 e2) #:transparent)  ; e1 in e2 sta izraza
(struct ce-potem-sicer (pogoj res nires) #:transparent) ; pogoj, res, nires hranijo izraze


(define (jais e)
  (cond [(konst? e) e]   ; vrnemo izraz v ciljnem jeziku
        [(bool? e) e]
        [(negiraj? e) 
         (let ([v (jais (negiraj-e e))])
           (cond [(konst? v) (konst (- (konst-int v)))]
                 [(bool? v) (bool (not (bool-b v)))]
                 [#t (error "negacija nepričakovanega izraza")]))]
        [(sestej? e) 
         (let ([v1 (jais (sestej-e1 e))]
               [v2 (jais (sestej-e2 e))])
           (if (and (konst? v1) (konst? v2))
               (konst (+ (konst-int v1) (konst-int v2)))
               (error "seštevanec ni številka")))]
        [(ce-potem-sicer? e) 
         (let ([v-test (jais (ce-potem-sicer-pogoj e))])
           (if (bool? v-test)
               (if (bool-b v-test)
                   (jais (ce-potem-sicer-res e))
                   (jais (ce-potem-sicer-nires e)))
               (error "pogoj ni logična vrednost")))]
        [#t (error "sintaksa izraza ni pravilna")]
        ))


; TESTI
;(jais (bool true))
;(jais (negiraj (bool true)))
;(jais (negiraj (konst 5)))
;(jais (sestej (konst 1) (ce-potem-sicer (bool true) (konst 5) (konst 10))))

;težava s sintakso
;(jais (negiraj (konst "lalala")))
;(jais (negiraj 1 2))

1.5.2.1.5 Razširitve

Razširitve preprostega jezika:

definiranje spremenljivk
definiranje lokalnih okolij
definiranje funkcij (funkcijskih ovojnic)
definiranje makrov

Potrebujemo znanje o delovanju teh elementov, ki ga pridobivamo od začetka predmeta.

1.5.2.2 Definicija spremenljivk in lokalnega okolja

Spremenljivko beremo vedno iz trenutnega okolja (torej potrebujemo okolje).

Okolje prenašamo v spremenljivki jezika 0, ki hrani vrednosti spremenljivk X:

okolje je na začetku prazno
primerna struktura je seznam parov (ime_spremenljivke . vrednost)
deklaracija nove spremenljivke doda v okolje nov par
shranjevanje najprej evalvira podani izraz, nato shrani vrednost

Dostop do spremenljivk:

preverjanje, ali je spremenljivka definirana
- če je, vrnemo vrednost
- sicer napaka

; dopolnimo interpreter tako, da imamo "register" - prostor za 
; eno samo spremenljivko, ki je evalviran poljuben izraz v jeziku JAIS

; dodamo deklaracijo 
(struct shrani (vrednost izraz) #:transparent)   ; shrani vrednost v register in evalvira izraz v novem okolju
(struct beri () #:transparent)                   ; bere register, ki je že evalviran v vrednost JAIS

; razširimo interpreter z okoljem, ki lahko hrani natanko eno spremenljivko in ki je od začetka prazno
(define (jais2 e) 
  (letrec ([jais (lambda (e env) 
                   (cond [(konst? e) e]   ; vrnemo izraz v ciljnem jeziku
                         [(bool? e) e]
                         ;[(shrani? e) (jais (shrani-izraz e) (shrani-vrednost e))]  ; ne zadošča, potrebna evalvacija vrednosti
                         [(shrani? e) (jais (shrani-izraz e) (jais (shrani-vrednost e) env))]
                         [(beri? e) env]
                         ; tukaj pride koda za negacijo
                         [(sestej? e) 
                          (let ([v1 (jais (sestej-e1 e) env)]
                                [v2 (jais (sestej-e2 e) env)])
                            (if (and (konst? v1) (konst? v2))
                                (konst (+ (konst-int v1) (konst-int v2)))
                                (error "seštevanec ni številka")))]
                         ; tukaj pride koda za ce-potem-sicer
                         [#t (error "sintaksa izraza ni pravilna")]))])
    (jais e null)))


; TESTI
;(jais2 (bool true))
;(jais2 (shrani (konst 5) (sestej (beri) (sestej (konst 1) (beri)))))
;(jais2 (shrani (konst 4) (konst 4)))
;(jais2 (shrani (konst 4) (beri)))
;(jais2 (shrani (sestej (konst 4) (konst 1)) (beri)))
;(jais2 (shrani (konst 4) (sestej (beri) (beri))))
; senčenje spremenljivk
;(jais2 (shrani (konst 4) 
;               (sestej (beri)
;                       (shrani (konst 2)
;                               (sestej (beri)
;                                       (sestej (konst 1) (beri)))))))

1.5.2.3 Definicija funkcij

Potrebujemo strukturo, ki bo hranila funkcijsko ovojnico (ne uporabljamo je v sintaksi programa, temveč samo pri izvajanju):

(struct ovojnica (okolje funkcija) #:transparent)

V okolje shranimo okolje, kjer je funkcija definirana (leksikalni doseg!), v funkcija pa funkcijsko kodo.

Kako izvesti funkcijski klic?

(klici ovojnica argument)

ovojnica mora biti funkcija, ki se je evalvirala v tip ovojnica, sicer napaka
argument mora biti vrednost (konstanta, boolean), ki je argument funkcije
izvajanje:
- ovojnica-funkcija evalviramo v okolju ovojnica-okolje, ki ga razširimo z:
- imenom in vrednostjo argumenta argument
- imenom funkcije, povezano z ovojnico (za rekurzijo)

; dopolnimo interpreter tako, da imamo interno strukturo za ovojnico,
; definicije spremenljivk in funkcijske klice
; omogočimo samo klice FUNKCIJ BREZ ARGUMENTOV

; struktura za ovojnico
(struct ovojnica (okolje fun) #:transparent)   ; funkcijska ovojnica: vsebuje okolje in kodo funkcije
; definicija funkcije v programu)
(struct funkcija (ime telo) #:transparent)     ; ime funkcije in telo
; funkcijski klic
(struct klici (ovojnica) #:transparent)        ; funkcijski klic


; razširimo interpreter z okoljem, ki je od začetka prazno
(define (jais3 e) 
  (letrec ([jais (lambda (e env) 
                   (cond [(funkcija? e) (ovojnica env e)]   ; definicijo funkcije shranimo kot ovojnico
                         [(klici? e) (let ([o (jais (klici-ovojnica e) env)])    ; potrebujemo klic interpreterja, ker je moramo funkcijo znotraj (klici...) preoblikovati v ovojnico
                                       (if (ovojnica? o)
                                           (jais (funkcija-telo (ovojnica-fun o))  ; izvedemo kodo, ki je v telesu funkcije
                                                 (ovojnica-okolje o))              ; kodo funkcije izedemo v okolju ovojnice (leksikalno)
                                                  ; okolje je potrebno še razširiti (glej predavanja)!!!
                                           (error "klic funkcije nima ustreznih argumentov")))]
                         [(konst? e) e]   ; vrnemo izraz v ciljnem jeziku
                         [(bool? e) e]
                         [(shrani? e) (jais (shrani-izraz e) (jais (shrani-vrednost e) env))]
                         [(beri? e) env]
                         ; tukaj pride koda za negacijo
                         [(sestej? e) 
                          (let ([v1 (jais (sestej-e1 e) env)]
                                [v2 (jais (sestej-e2 e) env)])
                            (if (and (konst? v1) (konst? v2))
                                (konst (+ (konst-int v1) (konst-int v2)))
                                (error "seštevanec ni številka")))]
                         ; tukaj pride koda za ce-potem-sicer
                         [#t (error "sintaksa izraza ni pravilna")]))])
    (jais e null)))


; TESTI
;(jais3 (funkcija "sestevanje" (sestej (beri) (konst 1))))                            ; samo prikaz interne predstavitve brez okolja
;(jais3 (shrani (konst 2) (funkcija "sestevanje" (sestej (beri) (konst 1)))))          ; samo prikaz interne predstavitve z okoljem
;(jais3 (klici (funkcija "sestevanje" (sestej (beri) (konst 1)))))  ; ni okolja
;(jais3 (shrani (konst 4) (klici (funkcija "sestevanje" (sestej (beri) (konst 1))))))
;(jais3 (shrani (konst 4) (shrani (funkcija "sestevanje" (sestej (beri) (konst 1))) 
;                                 (sestej (shrani (konst 1) (beri)) (klici (beri)))))) ; čeprav shrani povozi lokalno okolje, ima funkcija svoje v ovojnici

Možne razširitve:

rekurzivne funkcije
več formalnih argumentov
anonimne funkcije
optimizacija ovojnic

1.5.2.3.1 Optimizacija ovojnic

Okolje v ovojnici lahko vsebuje spremenljivke, ki jih funkcija ne potrebuje:

senčene spremenljivke iz zunanjega okolja
spremenljivke, ki so definirane v funkciji in senčijo zunanje
spremenljivke, ki v funkciji ne nastopajo

Ovojnice so lahko prostorsko zelo potratne, če so obsežne.

Rešitev: zmanjšamo število spremenljivk v okolju ovojnice na nujno potrebne.

Primeri nujno potrebnih spremenljivk:

(lambda (a) (+ a |b|bg:orange| |c|bg:orange|))

(lambda (a) (let ([b 5]) (+ a b |c|bg:orange|)))

(lambda (a) (+ |b|bg:orange| (let ([b |c|bg:orange|]) (* b 5))))

1.5.2.4 Definicija makrov

1.5.2.4.1 Implementacija makro sistema

Makro sistem:

nadomeščanje (neprijazne) sintakse z drugačno (lepšo)
širitev sintakse osnovnega jezika

V našem interpreterju (JAIS) lahko makro sistem implementiramo kar s funkcijami v jeziku Racket.

Primeri:

(define (in e1 e2)
   (ce-potem-sicer e1 e2 (bool #f)))

> (jais3 (in (bool #f) (bool #f)))
(bool #f)
> (jais3 (in (bool #f) (bool #t)))
(bool #f)
> (jais3 (in (bool #t) (bool #f)))
(bool #f)
> (jais3 (in (bool #t) (bool #t)))
(bool #t)

(define (vsota-sez sez)
   (if (null? sez)
      (konst 0)
      (sestej (car sez)
               (vsota-sez (cdr sez)))))

> (vsota-sez (list (konst 3) (konst 5)
   (konst 2)))

(sestej (konst 3) (sestej (konst 5)
(sestej (konst 2) (konst 0))))

Je tak makro sistem higieničen?

Ta makro sistem ni higieničen, ker ne preprečuje zajemanja spremenljivk (variable capture) in ne zagotavlja pravilnega leksikalnega obsega. Makri so implementirani kot preproste Racket funkcije, ki neposredno manipulirajo s kodo, brez mehanizmov za zagotavljanje unikatnih imen spremenljivk ali ohranjanje pravilnega obsega spremenljivk. Za primerjavo, pravi higienični makro sistemi (kot je Racketov syntax-case) zagotavljajo te varnostne mehanizme, vendar za ceno bolj kompleksne implementacije.

// TODO: (verify)

1.5.3 Funkcije z različnim številom argumentov

Poljubno število argumentov podamo z imenom spremenljivke brez oklepaja. V funkciji so vsi ti argumenti podani v seznamu, ki sledi ključni besedi lambda.

A lambda expression can also have the form:

(lambda rest-id
    body ...+)

That is, a lambda expression can have a single rest-id that is not surrounded by parentheses. The resulting function accepts any number of arguments, and the arguments are put into a list bound to rest-id.

(define izpisi
   (lambda sez
      (displayln sez)))

> (izpisi 1 2 3 4 5 6)
   (1 2 3 4 5 6)

(define vsotamulti
   (lambda stevila
      (apply + stevila)))

> (vsotamulti 1 2 3)
6
> (vsotamulti 1 2 3 11 33 -4)
46

Definiramo lahko tudi funkcijo z:

zahtevanim naborom osnovnih argumentov in
poljubnim številom dodatnih neobveznih argumentov

(lambda gen-formals
   body ...+)
                                             |tretja oblika sintakse|color:cornflowerblue|
      gen-formals = (arg ...)                         |arrow_start|
                  | rest-id
                  | (arg ...+ . rest-id)|arrow_end|

(define mnozilnik
   (lambda (ime faktor . stevila)
      (printf "~a~a~a~a"
               "Zivjo "
               ime
               ", tvoj rezultat je: "
               (map (lambda (x) (* x faktor)) stevila))))

> (mnozilnik "Frodo" 42 1 4 5 2 3)
Zivjo Frodo, tvoj rezultat je: (42 168 210 84 126)

1.5.4 Podajanje argumentov po imenih

1.5.4.1 Funkcije z imenovanimi argumenti

Argumente lahko podamo s ključnimi besedami:

notacija: #:beseda
takšni argumenti se pri klicu funkcije naslavljajo s ključno besedo in ne glede na podani vrstni red

Sintaksa:

A lambda form can declare an argument to be passed by keyword, instead of position. Keyword arguments can be mixed with by-position arguments, and default-value expressions can be supplied for either kind of argument:

(lambda gen-formals
   body ...+)

         gen-formals = (arg ...)          |arrow_start|
                     | rest-id
                     | (arg|arrow_end| ...+ . rest-id)

                  arg = arg-id
                     | [arg-id default-expr]             ; 2. sintaksa za podajanje s privzetimi vrednostmi
                     | arg-keyword arg-id                ; 1. sintaksa za podajanje s ključnimi besedami
                     | arg-keyword [arg-id default-expr] ; kombinacija 1. in 2.

1.5.4.2 Imenovani argumenti in privzete vrednosti

Podajanje s ključnimi besedami:

(define pozdrav
   (lambda (#:ime ime #:voscilo voscilo)
      (printf "~a~a~a~a" voscilo ", " ime "!")))

> (pozdrav #:ime "Helga" #:voscilo "Auf Wiedersehen")
Auf Wiedersehen, Helga!
> (pozdrav #:voscilo "Auf Wiedersehen" #:ime "Helga")
Auf Wiedersehen, Helga!

Podajanje s ključnimi besedami in/ali privzetimi vrednostmi:

(define mix
   (lambda ([ime "Frodo"] #:starost [starost 32])
      (printf "~a~a~a~a" ime " je star " starost " let.")))

> (mix)
Frodo je star 32 let.
> (mix "Jack")
Jack je star 32 let.
> (mix "Jack" #:starost 25)
Jack je star 25 let.
> (mix #:starost 25)
Frodo je star 25 let.
> (mix #:starost 25 "Janez")
Janez je star 25 let.

1.5.5 Primerjava ML in Racket

1.5.5.1 Statično preverjanje

Statično preverjanje so postopki za zavrnitev nepravilnega programa, ki so izvedeni po uspešni razčlenitvi programa in pred njegovim zagonom:

statično preverjanje:
- pravilna uporaba aritmetičnih izrazov
- pravilna semantika programskih konstruktov
- nedefinirane spremenljivke
- ujemanje vzorcev z vzorcem, ki se ponovi na dveh mestih
statično preverjanje NE obsega:
- preverjanje, ali bo prišlo do izjeme
- nepravilne aritmetične operacije (deljenje z 0)
- preverjanje semantičnih napak

Dinamično preverjanje: postopki za zavrnitev nepravilnega programa, ki se izvajajo med izvajanjem programa.

1.5.5.2 Primerjava ML in Racket - nadaljevanje

Razlike?

sintaksa
statična / dinamična tipizacija
ujemanje vzorcev / funkcije za preverjanje tipov in dostop do podatkov

Kakšna je relacija med številom veljavnih programov v obeh jezikih (vsi možni v SML vs vsi možni v Racket)?

Zakaj?

statični tipizator zavrne programe, ki ne ustrezajo semantičnim pravilom

Pozabimo na razlike v sintaksi in premislimo, kako iz enega od jezikov gledamo na lastnosti drugega.

Denimo da spodnja programa (oba sta veljavna v Racketu, nista pa veljavna v SML) implementiramo v SML:

(define (fun1 x) (+ x (car x)))

(define (fun2 x) (if (> x 10)
                  #t
                  (list 1 "zivjo")))

(* Poskus prevoda: fun1 sprejme parameter x, ki naj bi bil istočasno 
      število (zaradi +) in seznam (zaradi hd). *)

fun fun1 x = x + (hd x);

(* Poskus prevoda: fun2 sprejme parameter x (število za primerjavo), 
      a rezultat "if" združuje bool in seznam z različnimi tipi elementov. *)

fun fun2 x = if x > 10 then true else [1, "zivjo"];

➔ SML torej zavrača številne napačne programe (ki jih Racket ne zavrne), a na račun tega, da zavrne tudi programe, ki bi lahko bili veljavni.

1.5.6 Trdnost in polnost sistema tipov

Terminologija:

pozitiven primer programa: program, ki ima napako (+)
negativen primer programa: program brez napake (-)

Sistem je TRDEN (angl. sound), če nikoli ne sprejme pozitivnega programa (drugače povedano: vedno pravilno razpozna, da je pozitivni program res pozitiven)

vendar pa: ima lažno pozitivne primere (= pravilni/negativni programi, ki jih zaznamo kot nepravilne/pozitivne)

Sistem je POLN (angl. complete), če nikoli ne zavrne negativnega programa (drugače povedano: vedno pravilno razpozna, da je negativni program res negativen)

vendar pa: ima lažno negativne primere (= nepravilni/pozitivni programi, zaznani kot pravilni/negativni)

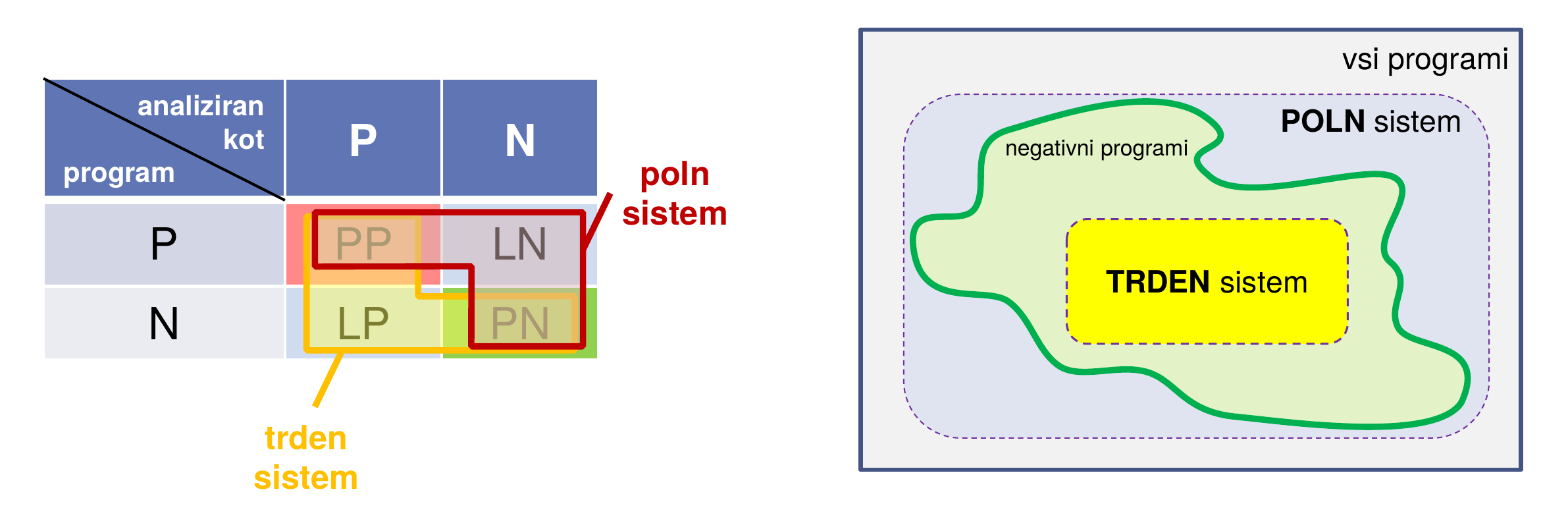
\ analiziran kot program \	P (analiziran da ima napako)	N (analiziran da nima napake)
P pozitiven (program ima napako)	PP (pravilno pozitiven)	LN (lažno negativen)
N negativen (program nima napake)	LP (lažno pozitiven)	PN (pravilno negativen)

1.5.6.1 Zakaj nepolnost?

Problem izvajanja statične analize, ki ugotovi vse troje:

ali je sistem trden,
ali je sistem poln in
ali je sistem ustavljiv

je NEODLOČLJIV (obstaja matematični teorem).

V praksi izberemo 2 od 3:

odločimo se za statično analizo, ki preverja ustavljivost in je trdna (ne sprejme nepravilnih programov)
kaj, če bi se odločili za analizo, ki preverja ustavljivost in je polna (torej ni trdna, sprejme tudi nepravilne programe → sistem s šibkim tipiziranjem (weak typing)

Tudi sistem tipov v SML je trden, vendar ni poln:

trdni/nepolni sistemi tipov so praksa
primer lažno pozitivnega primera (zavrnjeni primeri, ki ne povzročajo težav)?

fun f x = if true then 0 else 4 div "hello"

1.5.6.2 Šibko tipiziranje

Šibko tipiziranje (angl. weak typing).

Sistem, ki:

je POLN (dopušča lažne negativne primere)
med izvajanjem se lahko zgodi napaka (potrebno preverjanje)
sistem izvaja malo statičnih ali dinamičnih preverjanj
rezultat: neznan?
C / C++

Prednosti šibko tipiziranih sistemov:

“omogočajo večje programersko mojstrstvo?”
lažja implementacija programskega jezika (ni avtomatskih preverjanj)
večja učinkovitost (ni porabe časa za preverjanja; ni porabe prostora za oznake podatkovnih tipov)

1.5.6.3 Prednosti obeh sistemov

Kriterij	Statično preverjanje	Dinamično preverjanje
kombiniranje podatkovnih tipov v seznamih in vejah programa	ni možno, vendar pa zato v programu vemo, katere tipe seznamov in funkcij lahko pričakujemo 🟰	je možno, moramo pa v programu uporabiti vgrajene predikate za preverjanje tipov 🟰
sprejemanje množice programov	zavrača pravilne programe ❗	sprejema več pravilnih programov ✅
čas ugotavljanja napak	napake v programu ugotovimo zgodaj ✅	napake ugotovi šele med izvajanjem ❗
hitrost izvajanja	prihrani na prostoru in času, ker ne označuje spremenljivk z značkami posameznih podatkovnih tipov (at runtime) ✅	prevajalnik potrebuje več prostora in časa za označevanje spremenljivk z značkami, programer ima več dela ❗
večkratna uporabnost programske kode	manjša, vendar s tem večje nadzorovanje napak ❗	večja, vendar odpira možnosti za več napak v programu ✅
prototipiranje novih programov	težje, potrebno določiti podatkovne tipe vnaprej; vendar pa lažje nadzorovanje vpliva sprememb na delovanje obstoječe kode 🟰	preprosteje, vendar šibkejše nadzorovanje vpliva sprememb na obstoječo kodo 🟰

Legenda:

✅ : Boljše
❗ : Negativno
🟰 : Nevtralno

Kaj je boljše?

smiselno je najti kompromis: del preverjanja se izvede statično, del dinamično
programski jeziki uporabljajo kombinacijo obojega

1.5.7 Primerjava funkcijskega in OU programiranja

1.5.7.1 Povezava med FP in OUP

Program lahko analiziramo glede na uporabo podatkovnih tipov in funkcij:

“Narediti program” pomeni “izpolniti” zgornjo tabelo s programsko kodo za vsak podatkovni tip in funkcijo, ki jo uporabljamo:

Funkcijsko programiranje: program je množica funkcij, ki so zadolžene vsaka za svojo operacijo.

Objektno-usmerjeno programiranje: program je množica razredov, ki v sebi vsebujejo različne operacije nad primerki razreda.

FP in OUP sta torej le drugačni perspektivi na izdelavo istih programov.

Katerega izbrati?

osebni programerski stil
upoštevati je potrebno način razširjanja programa

Razširjanje programa z novo kodo:

funkcijsko programiranje:
- če dodamo novo funkcijo, moramo v njej pokriti vse konstruktorje za podatkovni tip (sicer nas prevajalnik opozori) ✅
- če samo razširimo podatkovni tip, moramo dopolniti vse funkcije s kodo za delo s tem tipom ❗
objektno-usmerjeno programiranje:
- če dodamo novo funkcijo za delo s podatkovnimi tipi, jo moramo implementirati na novo v vseh ločenih razredih (ne upoštevajmo možnosti dedovanja) ❗
- če implementiramo novi razred (podatkovni tip), v njemu implementiramo vse možne funkcije (metode) za delo s tem razredom ✅

1.6 Funkcijsko programiranje v Pythonu

1.6.1 FP v Pythonu

Python ni čisti funkcijski jezik, nudi različne paradigme programiranja. Ima zmožnosti funkcijskega programiranja:

anonimne funkcije
funkcije višjega reda
map(), reduce(), filter()
izpeljani seznami
iteratorji
generatorji
memoizacija
currying
in še druge…

1.6.1.1 Funkcije

1.6.1.1.1 Anonimne funkcije

# poimenovana funkcija
def kvadrat(x):
   return x**2

ali

# anonimna funkcija
kvadrat = lambda x: x**2

Na predavanjih:

(lambda x: x*x)(30)

1.6.1.1.2 Funkcije višjega reda

Definicija funkcij višjega reda:

def izbira(ocena):
   if ocena >5:
      return lambda dan: "V " + dan + " praznujemo."
   else:
      return lambda tocke, datum:
         "Dobil sem samo " + str(tocke)
         + " tock. Dne " + datum
         + " je naslednji rok."
   
>>> rezultat = izbira(5)
>>> rezultat(33, "1.1.2012")
'Dobil sem samo 33 tock. Dne 1.1.2012 je naslednji rok.'

>>> rezultat = izbira(10)
>>> rezultat("petek")
'V petek praznujemo.'

Uporaba vgrajenih funkcij:

>>> map(lambda x: x**2, range(1,5))
[1, 4, 9, 16]
>>> filter(lambda x: x%2==0, range(10))
[0, 2, 4, 6, 8]
>>> reduce(lambda x,y: x+y, [47, 11, 42, 13])
113

S predavanj:

# primeri MAP, REDUCE, FILTER

# 1. seznam kvadratov
list(map(lambda x: x**2, [1,2,3,4,5]))

# 2. izbiranje samo sodih
list(filter(lambda x: x%2==0, range(10)))

# 3. seštevanje seznama
from functools import reduce
reduce(lambda x,y: x+y, [47, 11, 42, 13], 0)

1.6.1.1.3 Memoizacija

S predavanj:

from functools import lru_cache

@lru_cache(maxsize=None)
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)
fib(34)

1.6.1.1.4 Funkcijske ovojnice

Ovojnica = telo funkcije + okolje

Možni načini uporabe:

uporaba privzetih vrednosti
ovijanje funkcije v zunanjo funkcijo
uporaba posebnih razredov in orodij (closure, Bindings)

dinamični doseg zaprtje s privzeto vrednostjo
(“zapečena” v funkcijo) zaprtje z ovijanjem funkcije
v zunanjo funkcijo

>>> N = 10
>>> def pristejN(i):
      return i+N
>>> pristejN(7)
17
>>> N = 20
>>> pristejN(7)
27

brez uporabe funkcijske ovojnice

>>> N = 10
>>> def pristejN(i, n=N):
      return i+n
>>> pristejN(7)
17
>>> N = 20
>>> pristejN(7)
17
>>> pristejN(7, 2)
9

ovojnica s privzeto vrednostjo
n se shrani ob definiciji
še vedno pa jo lahko override-amo ob klicu

>>> N = 10
>>> def pristejNx(N):
      def pristejN1(i):
          return i+N
      return pristejN1
>>> moja = pristejNx(12)
>>> moja(5)
17
>>> N = 20
>>> moja(5)
17

ovoj funkcije
N se zapeče ob klicu funkcije pristejNx

1.6.1.2 Seznami

1.6.1.2.1 Sestavljeni seznami

Način avtomatskega sestavljanja seznamov v skladu z matematično formulacijo.

Lahko običajno nadomestijo map, filter in reduce,

\[ A = {f(x) | x ∈ D, \text{pogoj}(x)}\text{, npr. }A = {x² | x ∈ ℕ, 5 ≤ x ≤ 15} \]

Sestavljen seznam (list comprehension):

[funkcija(x) for x in D if pogoj(x)]

je enakovredno

r = []
for e in D:
    if pogoj(e):
        r.append(funkcija(e))

Primer:

def prasteviloS(n):
    return not [x for x in range(2, n) if n % x == 0]

k = [4,25,100,10000,196]

#seznam kvadratnih korenov
from math import sqrt
[sqrt(x) for x in k]

#seznam kvadratov
[x**2 for x in k]

#seznam kvadratov, ki so med 10.000 in 100.000
[x**2 for x in k if 10000 <= x**2 <= 100000]

#seznam obrnjenih stevil od konca nazaj
[int(str(x)[::-1]) for x in k]

#vsota kvadratov vseh palindromnih stevil do 1000
sum([x**2 for x in range(1,1001) if x==int(str(x)[-1::-1])])
[x for x in range(1,1001) if x==int(str(x)[-1::-1])]

#podan je seznam imen. Kaksna je njihova povprecna dolzina?
imena = ["Ana", "Berta", "Cilka", "Dani", "Ema"]
sum([len(ime) for ime in imena]) / len(imena)

1.6.1.2.2 Gnezdeni sestavljeni seznami

Primer: poiščimo pitagorejske trojčke (za njih velja x2 + y2 = z2)

[(x,y,z) for x in range(1,30)
   for y in range(x,30)
      for z in range(y,30)
         if x**2 + y**2 == z**2]

Rezultat:

[(3, 4, 5), (5, 12, 13), (6, 8, 10),
(7, 24, 25), (8, 15, 17), (9, 12, 15),
(10, 24, 26), (12, 16, 20), (15, 20, 25),
(20, 21, 29)]

1.6.1.3 Sestavljene množice in slovarji

# obstajajo tudi sestavljene MNOŽICE
squares_set = {x**2 for x in [1,2,3,4,5]}
print(squares_set)
print(type(squares_set))

# rezultat:
{16, 1, 9, 25, 4}
<class 'set'>


# obstajajo tudi sestavljeni SLOVARJI
squares_dict = {x : x**2 for x in [1,2,3,4,5]}
print(squares_dict)
print(type(squares_dict))

# rezultat:
{1: 1, 2: 4, 3: 9, 4: 16, 5: 25}
<class 'dict'>

1.6.1.4 Dekoratorji

1.6.1.4.1 Dekoratorji kot funkcije višjega reda

Dekorator: funkcija, ki sprejme neko funkcijo (f) in jo vrne ovito v ovoj (wrapper):

def decor(f):
   def wrapper():
      print("Inside wrapper")
      f()
   return wrapper

Pripis dekoratorja funkciji:

@decor      # dekorator
def f():    # definicija dekorirane funkcije
    print("Inside function")
    f()

Klic dekorirane funkcije: f()

Zelo podobno (vendar ne čisto enako kot): decor(f)()

# uporaba dekoratorja nad funkcijo f
g = decor(f)
#g()
# opomba: ovit je samo prvi klic funkcije f(), rekurzivni pa ne


# SINTAKTIČNA OLEPŠAVA ZA uporabo dekoratorja (združimo klic dekoratorja in definicijo funkcije)
# razlika: oviti so vsi klici funkcije f() (tudi rekurzivni)
def decor(f):
    def wrapper():
        print("Inside wrapper")
        f()
    return wrapper

@decor
def f():
    print("Inside function")
    #f() # Če tole pustimo notri se izvaja rekurzivno v neskončnost

f()
- Inside wrapper
- Inside function

f.__name__
- 'wrapper'

# orodje za prenos metapodatkov (dokumentacija, ime) notranje funkcije v zunanjo
from functools import wraps
def decor(f):
    @wraps(f)
    def wrapper():
        print("Inside wrapper")
        f()
    return wrapper

@decor
def f():
    print("Inside function")
    f()

f()
f.__name__

1.6.1.4.2 Dekoratorji in argumenti funkcij

Pri klicu funkcije lahko v Pythonu podamo pozicijske in imenovane argumente:

Presežek nepodanih pozicijskih argumentov je shranjen v spremenljivko, zapisano z eno zvezdico (npr. *args), ki je terka.
Presežek nepodanih imenovanih argumentov je shranjen v spremenljivko, zapisano z dvema zvezdicama (npr. **kwargs), ki je slovar.

def test(a, b, c, *args, **kwargs):
   return (args, kwargs)

>>> test(1, 2, 3, 4, 5, 6, x=5, y=12)
((4, 5, 6), {'x': 5, 'y': 12})

Pravilni prenos argumentov v dekorirano funkcijo:

def decor(f):
   def wrapper(*args,**kwargs):
      print("Kličem funkcijo %s" % f.__name__)
      f(*args,**kwargs)
   return wrapper

@decor
def funk(arg1, arg2, ..., argn):
   ...

# PRIMER: uporaba argumentov funkcije f znotraj dekoratorja (nedelujoč primer)
def decor(f):
    def wrapper():
        print("Kličem funkcijo %s" % f.__name__)
        f()
    return wrapper

@decor
def f(n):
    if n>0:
       print("f(%d)" % n)
       f(n-1)

#f(5)


# uporabimo spremenljivki *args in **kwargs, ki hranita neuporabljene pozicijske in imenovane argumenta
def test(a, b, c, *args, **kwargs):
    return (args, kwargs)
test(1,2,3)
test(1,2,3,4,5,6,x=5,y=12)

def test1(*args):
    return (args)

test1(1,2,3)
test1(1,2,3,4,5,6,x=5,y=12)

def test2(args):
    return (args)


# PRIMER: popravljena uporaba argumentov funkcije f znotraj dekoratorja (deluje)
def decor(f):
    def wrapper(*args,**kwargs):
        print("Kličem funkcijo %s" % f.__name__)
        f(*args,**kwargs)
    return wrapper

@decor
def funk(n):
    if n>0:
       print("funk(%d)" % n)
       funk(n-1)

# funk(5)


# PRIMER: DEKORATOR ZA IMPLEMENTACIJO MEMOIZACIJE
def memoize(f):
    memoizer = {}           # slovar parov že videnih rešitev v obliki argument:vrednost
    def wrapper(*args):
        if args not in memoizer:
            memoizer[args] = f(*args)
            print(memoizer)
        return memoizer[args]
    return wrapper

@memoize
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)

print(fib(34))

1.6.1.5 Currying

1.6.1.5.1 Currying funkcij višjega reda

Denimo, da želimo definirati obliko naslednje funkcije, ki uporablja currying:

def f(a,b,c):
   return a+b+c

f(a)
f(a)(b)
f(a)(b)(c)

Ročna definicija:

def f(x, *args):
   def f1(y, *args):
      def f2(z):
         return x+y+z      # sprejme z in izračuna vsoto x+y+z
      if args:                # |
         return f2(*args)     # | sprejme y in preda izračun f2
      else:                   # |
         return f2            # |
   if args:             # |
      return f1(*args)  # | sprejme x in preda izračun f1
   else:                # |
      return f1         # |

# za zgornji primer

f1 = f(1)
print(f1)
f2 = f1(2)
print(f2)
f2(3)
f(1)(2)(3)

1.6.1.5.2 Currying: preprosteje

Uporabimo lahko modul pymonad.

Namestitev (ukazna vrstica):

pip install pymonad

Nato uporabimo dekorator @curry

from pymonad import curry

@curry
def f(a,b,c):
   return a+b+c

1.6.1.6 Iterator

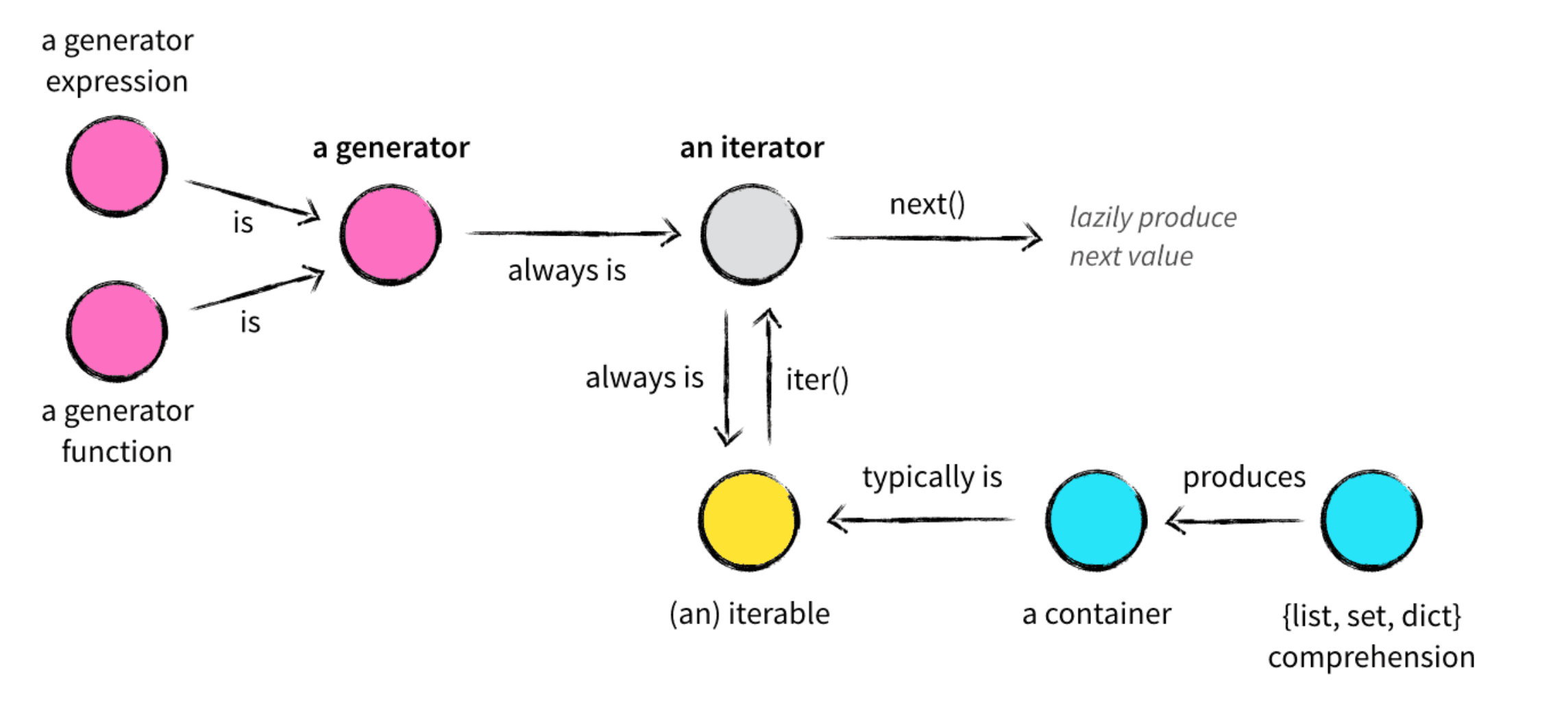
1.6.1.6.1 Iteratabilni objekt (razred)

Iterator je objekt, ki predstavlja tok podatkov in vrača posamezne elemente iterabilnega objekta:

zakasnjeno izvajanje

Iterabilen razred implementira metodo __iter__() - vrne objekt-iterator nad tem razredom.

Razred lahko implementira tudi metodo __next__() - vrne naslednji element do izčrpanja (StopIteration) ali v neskončnost.

Premikanje nazaj ni možno.

Funkcija iter(objekt) - pretvorba iterabilnega objekta v iterator.

1.6.1.6.2 Iterator - nadaljevanje

Funkcija iter(objekt) pretvori iterabilni objekt v iterator:

# izdelava lastnega iteratorja
class Counter:
   def __init__(self, low, high):
      self.current = low
      self.high = high
   
   def __iter__(self):
      return self
   
   def __next__(self):
      if self.current > self.high:
         raise StopIteration
      else:
         self.current += 1
         return self.current - 1

for c in Counter(3, 8):
   print(c)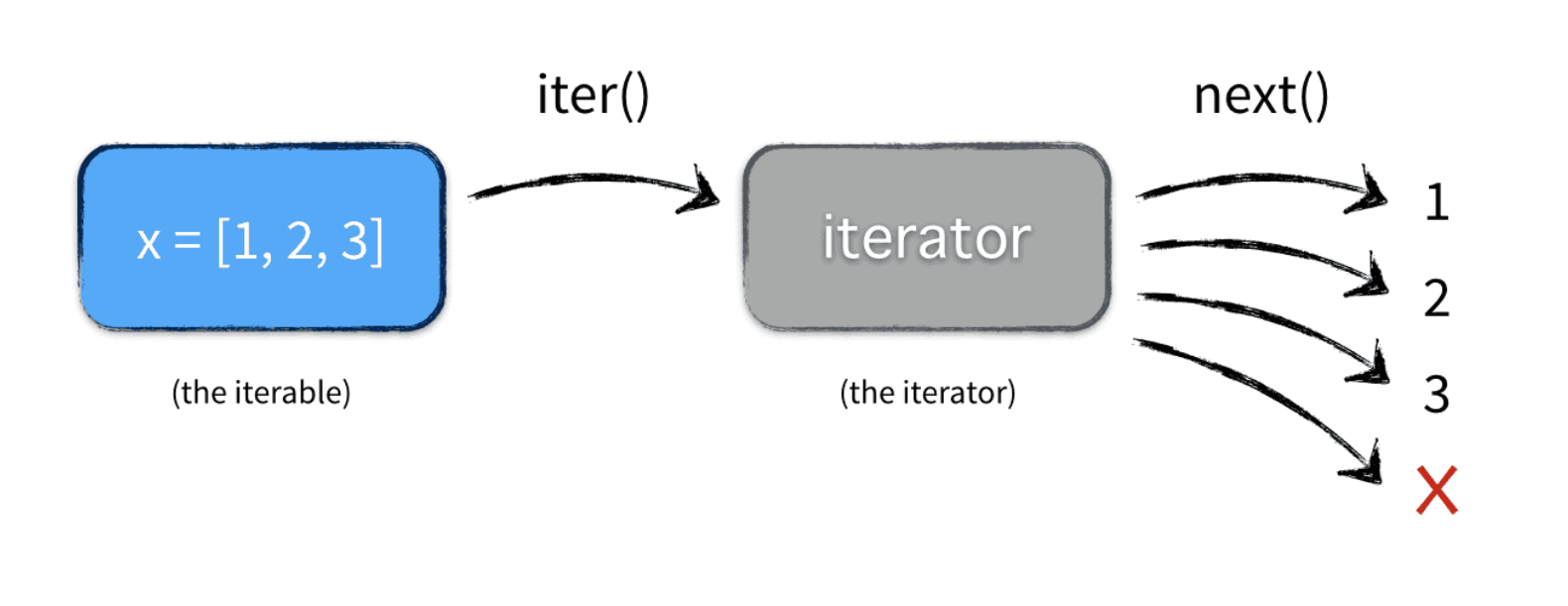

# pretvorba seznama v iterator
>>> L = ["danes", 155, True, "a"]
>>> for c in L:
      print(c)
danes
155
True
a

>>> i = iter(L)
>>> i.__next__()
danes
>>> i.__next__()
155
>>> i.__next__()
True
>>> i.__next__()
'a'
>>> i.__next__()
Traceback (most recent call last):
  File "<python-input-22>", line 1, in <module>
    i.__next__()
    ~~~~~~~~~~^^
StopIteration

1.6.1.6.3 Iterabilni objekti

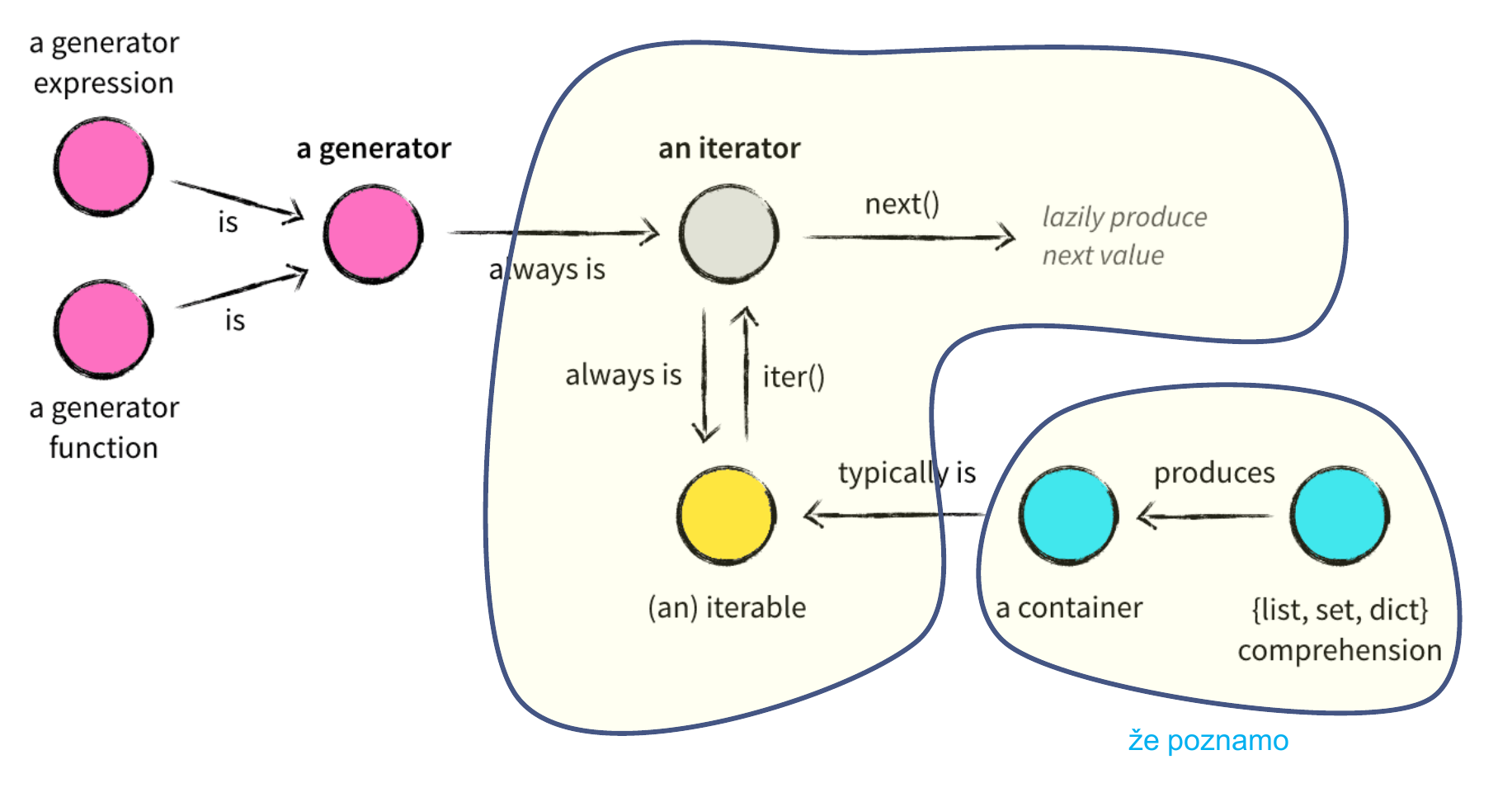
1.6.1.6.4 Generator

Generatorji so tudi iteratorji.

Poenostavijo zapis iteratorja:

so funkcije, ki iterirajo preko toka vrednosti in omogočajo zakasnjeno izvajanje izrazov:
- izvajanje funkcije se lahko zaustavi in nadaljuje
- lokalno okolje funkcije se ohranja tudi ob zaustavitvi
- stavek yield zaustavi izvajanje in preda kontrolo klicočemu okolju
- funkcija nadaljuje z izvajanjem ob klicu metode .__next__()
- generiranje se zaključi s stavkom return ali izjemo StopIteration
- generatorju lahko podamo argument z metodo .send(arg)
zgodovinsko: do Pythona 3 sta obstajala range(min,max) in xrange(min,max) (takojšnje in leno evalviran range)

def genstevec(max):
   i = 0
   while i<max:
      yield i
      i += 1

def genstevec(max):
   i = 0
   while i<max:
      vnos = (yield i)
      if vnos == None:
         i += 1
      elif vnos>=max:
         raise StopIteration
      else:
         i = vnos

1.6.1.6.5 Generatorski izrazi

Krajši način za specifikacijo iteratorjev

Sintaksa podobna sestavljenim seznamom/množicam/slovarjem.

Nekoliko okrnjena funkcionalnost.

>>> def Squares(max):
      i = 0
      while i<max:
         yield i*i
         i += 1

>>> g1 = Squares(10)
>>> print(g1)
<generator object Squares at 0x7fd4cf713d00>

>>> list(g1)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

#generator: Fibonaccijeva steila
#koncni generator
def fibonacci(n):
    a = b = 1
    for i in range(n):
        yield a
        a, b = b, a+b

#neskoncni generator
def fibonacciAll():
    a = b = 1
    while True:
        yield a
        a, b = b, a+b

g2 = (x*x for x in range(10))

# sestavljeni seznam
>>> g2 =[x*x for x in range(10)]
>>> print(type(g2))
<class 'list'>
>>>print(g2)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

# generatorski izraz
>>> g3 = (x*x for x in range(10))
>>> print(g3)
<generator object <genexpr> at 0x7fd4cf3b6670>
>>> list(g3)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]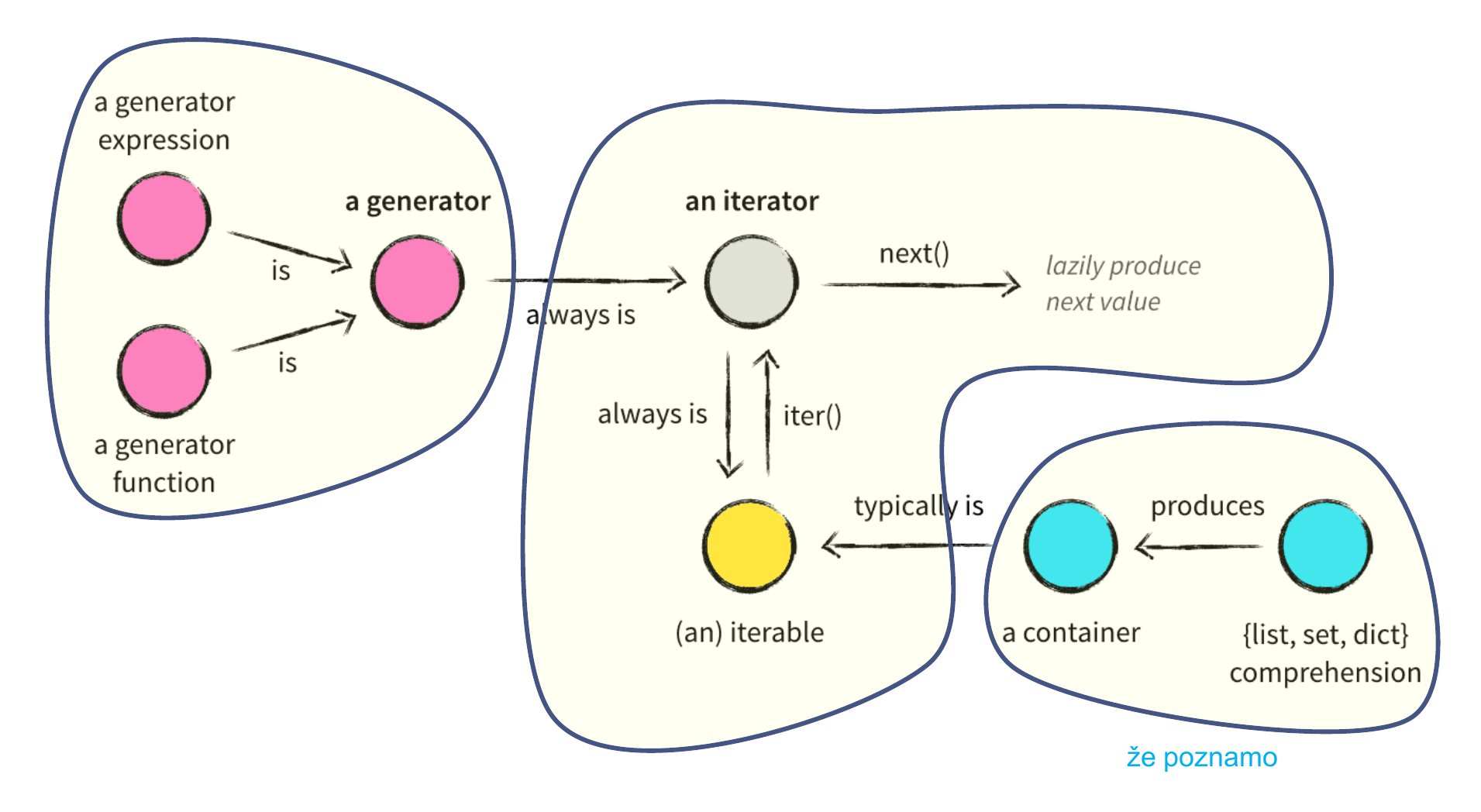

1.6.2 Zaključek

Cilji predmeta:

postati boljši programer
- naučiti se novih konceptov (polimorfizem, zakasnjena evalvacija, tokovi, memoizacija, funkcije višjega reda, ovojnice, delna aplikacija, currying, …)
razumeti delovanje programskega jezika
- pridobiti sposobnost hitrega učenja novega programskega jezika
- ločiti bolj in manj elegantne implementacije
izstopiti iz okvira objektno-usmerjenega programiranja
- razumeti funkcijsko in objektno-usmerjeno paradigmo
naučiti se funkcijskega programiranja. Njegove prednosti:
- bolj abstrakten opis problema
- možnost paralelizacije
- brez mutacije vrednosti (manj semantičnih napak)
- lažje testiranje (testi enot)
- lažji formalni dokaz pravilnosti
dojeti “motivacijski članek” ☺

2 Vaje

2.1 0. laboratorijske vaje

2.1.1 Snov

2.1.1.1 Uporaba podpičij

Če v sml datotekah ne uporabimo podpičij ;, bo interpreter interpretiral celotno datoteko v “enem kosu”. Kar pomeni, da bo izpis interpreterja (v nekaterih primerih) neprijazen do uporabnika. Poleg tega je razhroščevanje težje.

Zato bomo za vsako definicijo funkcije in vezavo spremenljivk pisali podpičje.

fun <ime funkcije> <argumenti> = <telo funkcije>;
val <ime spremenljivke> = <izraz>;

2.1.1.2 Osnovni tipi in imena spremenljivk

Osnovni tipi (ki jih bomo mi uporabljali):

Logične vrednosti bool: false : bool, true : bool.
Cela števila int (?.int) iz modulov Int (Int.int) in LargeInt (LargeInt.int): ~1337 : Int.int, 1234567891011121314151617181920 : LargeInt.int. Privzeti tip za int je tip Int.int.
Števila v plavajoči vejici real iz modula Real: 2.718 : real.

Pri izbiri imen spremenljivk (in funkcij) moramo paziti naslednje:

Ime spremenljivke ni ena izmed naslednjih rezerviranih besed:

abstype and       andalso   as     case  do       datatype   else
end     eqtype    exception fn     fun   functor  handle     if
in      include   infix     infixr let   local    nonfix     of
op      open      orelse    raise  rec   sharing  sig        signature
struct  structure then      type   val   where    with       withtype
while   (         )         [      ]     {        }          ,
:       :>        ;         ...    _     |        =          =>
->      #

Je lahko zaporedje alfa-numeričnih znakov, ki lahko vsebuje tudi opuščaje ' in podčrtaje _. Prvi znak v imenu ne sme biti opuščaj ali podčrtaj. Na primer: val jaz_sem_pa_poseben' = "jaz sem pa poseben".
Je lahko samo _ (anonimna spremenljivka, o tem več kasneje).
Je lahko poljubno zaporedje posebnih znakov: npr. val -><- = false.

Imena funkcij in spremenljivk ponavadi pišemo z malo začetnico. Imena, ki se začnejo z velikimi začetnicami rezerviramo za poimenovanje konstruktorjev, modulov, … (več o tem kasneje).

Komentarje pišemo tako: (* <tukaj pride komentar - lahko se razteza čez več vrstic> *).

2.1.1.3 Nekaj integriranih funkcij, funkcije iz “baznih knjižnic” in prioritete infiksnih operatorjev

Nekaj infiksnih funkcij (večja številka pomeni višjo prioriteto, operatorji so levo asociativni):

infix 0 before (* trenutno ni pomembno *)
infix 3 o := (* trenutno ni pomembno *)
infix 4 = <> > < >= <= (* neenako, večje, majše, večje ali je-enako, manjše ali je-enako *)
infixr 5 :: @ (* trenutno ni pomembno *)
infix 6 + - ^ (* seštevanje, odštevanje, stikanje nizov *)
infix 7 * / div mod quot rem (* množenje, deljenje, celoštevilsko deljenje, ostanek pri deljenju z div, odrezano deljenje, ostanek pri deljenju z quot *)

Znak za enakost = ima več pomenov. Lahko je del sintakse ali pa predstavlja funkcijo - “ekvivalenco”. Opazuj naslednji primer:

val ali_sta_enaka (a: int, b: int): bool = a = b

Operator = deluje za “veliko” tipov. Ne pa za vse (pri nadaljnjih predvajanjih boste spoznali v čem je problem). Tak primer je real.

val ali_sta_enaka (a : real, b : real): bool = a = b (* to ne gre *)
val ali_sta_enaka' (a : real, b : real): bool = Real.== (a, b) (* PAZI na zaokroževanje *)

Še nekaj drugih logičnih operatorjev:

Negacija not: not true.
Konjunkcija andalso: 1 > 0 andalso true.
Disjunkcija orelse: false orelse true.

Do funkcij in spremenljivk v nekem modulu odstopamo kot <ime modula>.<ime funkcije>. Primera: Int.max (Int.min (a, b), c) in Math.pow (Math.e, ~ Math.pi / 2.0)

2.1.1.4 Priprava (primitivnih) testov

Naravno je, če teste pišemo v ločeni datoteki npr. testi.sml, saj jih lahko poženemo skupaj z programom program.sml.

$ sml program.sml testi.sml

Ustreznost tipa funkcije lahko potestiramo na naslednji način:

val _ : <željen tip funkcije> = <ime funkcije>

Enotski testi so najbolj primitivna oblika testiranja implementacije neke funkcije <ime funkcije>. V SML jih najlažje (s trenutnim znanjem) realiziramo tako:

val <ime testa> = <ime funkcije> <argumenti> = <pričakovan rezultat>

Vrednost spremenljivke <ime testa> bo true, če funkcija <ime funkcije> prestane dani test.

Poglejmo si en primer testiranje funkcije podvoji_in_negiraj.

(* v datoteki program.sml *)
fun podvoji_in_negiraj (a: int): int = ~ 2 * a;

(* v datoteki program-tests.sml *)
val _ : int -> int = podvoji_in_negiraj; (* test tipa *)
val test1 = podvoji_in_negiraj 1 = ~2;
val test2 = podvoji_in_negiraj 0 = 0;
val test3 = podvoji_in_negiraj ~21 = 42;

Lahko bi imeli napredne test z uporabo SML CM, ampak mi lahko verjamete na besedo, da tega ne želite početi.

2.1.2 Naloge za oddajo

V programskem jeziku SML implementirajte naslednje funkcije (poskusi se izogniti uporabi if stavka):

(* Vrne naslednika števila `n`. *)
fun next (n : int) : int

(* Vrne vsoto števil `a` in `b`. *)
fun add (a : int, b : int) : int

(* Vrne true, če sta vsaj dva argumenta true, drugače vrne false *)
fun majority (a : bool, b : bool, c : bool) : bool

(* Vrne mediano argumentov - števila tipa real brez (inf : real), (~inf : real), (nan : real) in (~0.0 : real)
   namig: uporabi Real.max in Real.min *)
fun median (a : real, b : real, c : real) : real

(* Preveri ali so argumenti veljavne dolžine stranic nekega trikotnika - trikotnik ni izrojen *)
fun triangle (a : int, b : int, c : int)  : bool

Oddajte eno datoteko z imenom 00.sml.

Primer testov, datoteka 00-tests.sml:

(* use "00.sml"; *)
val _ = print "~~~~~~~~ next ~~~~~~~~\n";
val test_type: int -> int = next;
val test = next (~1) = 0;

val _ = print "~~~~~~~~ add ~~~~~~~~\n";
val test_type: int * int -> int = add;
val test = add (~1, 1) = 0;

val _ = print "~~~~~~~~ majority ~~~~~~~~\n";
val test_type: bool * bool * bool -> bool = majority;
val test = majority (false, false, true) = false;

val _ = print "~~~~~~~~ median ~~~~~~~~\n";
val test_type: real * real * real -> real = median;
val == = Real.==;
infix ==;
val test = median (1.1, ~1.0, 1.0) == 1.0;

val _ = print "~~~~~~~~ triangle ~~~~~~~~\n";
val test_type: int * int * int -> bool = triangle;
val test = triangle (~1, ~1, ~1) = false;

2.2 1. laboratorijske vaje

2.2.1 Snov

2.2.1.1 Terke

Za enkrat poznamo dva načina za dostopanje do elementov terk:

z uporabo funkcij #1, #2, … ali pa
z eksplicitno definiranim argumentom funkcije ob sami definiciji fun (a1, a2, a3, ...) = <telo funkcije>.

Implementiraj funkcijo fun implies (z : bool * bool) : bool na ta dva načina.

2.2.1.2 Lokalno okolje

Sintaksa za lokalno okolje je let <vezave spremenljivk in definicije funkcij> in <uporaba definiranih funkcij in spremenljivk> end.

Dopolni spodnjo funkcijo partition (x : int, xs : int list), ki vrne dva seznama (kot terko). Prvi seznam so števila seznama xs, ki so strogo manjša od števila x. Drugi seznam pa vsebuje preostala števila seznama xs. Funkcija naj ohrani vrsti red števil.

fun partition (x, xs) =
let
    fun partition (xs, l, r) =
        (* manjka telo funkcije *)
in
    partition (xs, [], [])
end

Sprogramiraj funkcijo quickselect s pomočjo funkcije partition. Vrne naj (k + 1)-to najmanjše število seznama xs (predpostaviš lahko, da je k manjsi od dolžine seznama xs).

fun quickSelect (k : int, xs : int list) : int
(* ali pa fun quickSelect (k : int, xs : int list) : int option *)

Pomagaj si z nasledjo psevdokodo (seznami imajo lahko podvojene elemente!):

2.2.2 Naloge za oddajo

V programskem jeziku SML implementirajte naslednje funkcije (brez uporabe “napredih” funkcij za delo s seznami):

(*  Vrne fakulteto števila n, n >= 0. *)
fun factorial (n : int) : int

(*  Vrne n-to potenco števila x, n >= 0. *)
fun power (x : int, n : int) : int

(*  Vrne največjega skupnega delitelja pozitivnih števil a in b, a >= b. *)
fun gcd (a : int, b : int) : int

(*  Vrne dolžino seznama. *)
fun len (xs : int list) : int

(*  Vrne SOME zadnji element seznama. Če je seznam prazen vrne NONE. *)
fun last (xs : int list) : int option

(*  Vrne SOME n-ti element seznama. Prvi element ima indeks 0. Če indeks ni veljaven, vrne NONE. *)
fun nth (xs : int list, n : int) : int option

(*  Vrne nov seznam, ki je tak kot vhodni, le da je na n-to mesto vrinjen element x. Prvo mesto v seznamu ima indeks 0. Indeks n je veljaven (0 <= n <= length xs). *)
fun insert (xs : int list, n : int, x : int) : int list

(*  Vrne nov seznam, ki je tak kot vhodni, le da so vse pojavitve elementa x odstranjene. *)
fun delete (xs : int list, x : int) : int list

(*  Vrne obrnjen seznam. V pomoč si lahko spišete še funkcijo append, ki doda na konec seznama. *)
fun reverse (xs : int list) : int list

(*  Vrne true, če je podani seznam palindrom. Tudi prazen seznam je palindrom. *)
fun palindrome (xs : int list) : bool

Oddajte eno datoteko z imenom 01.sml.

2.3 2. laboratorijske vaje

2.3.1 Snov

2.3.1.1 Lastni podatkovni tipi

2.3.1.1.1 Ujemanje vzorcev

Za naslednji podatkovni tip yesNo želimo implementirati funkcijo toString : yesNo -> string, ki vrednost tega tipa spremeni v niz.

datatype yesNo = Yes | No

To lahko naredimo z ujemanjem vzorcev na (vsaj) dva načina:

z uporabo rezerviranih besed case, of, | in =>,

fun toString x = case x of Yes => "Da" | No => "Ne"

ali pa z ujemanjem vzorcev že ob sami deklaraciji funkcije.
```
fun toString Yes = "Da" | toString No = "Ne"
```

2.3.1.1.2 Kvartopirska

datatype barva = Kriz | Pik | Srce | Karo
datatype stopnja = As | Kralj | Kraljica | Fant | Stevilka of int

type karta = stopnja * barva

(* Kakšne barve je karta? *)
fun barvaKarte (k : karta) : barva

(* Ali je karta veljavna? *)
fun veljavnaKarta (k : karta) : bool

(* Koliko je vredna karta? *)
fun vrednostKarte (k : karta) : int

(* Kolikšna je vrednost vseh kart v roki? *)  
fun vsotaKart (ks : karta list) : int

(* Ali imam v roki karte iste barve? *)
fun isteBarve (ks : karta list) : bool

Rešitve:

fun barvaKarte ((_, b) : karta) = b;

fun veljavnaKarta ((Stevilka i, _) : karta) = i >= 2 andalso i <= 10 | veljavnaKarta _ = true;

fun vrednostKarte ((s, _) : karta) = case s of Stevilka i => i | As => 11 | _ => 10;

fun vsotaKart (nil : karta list) = 0 | vsotaKart (c :: cs) = vrednostKarte c + vsotaKart cs;

fun isteBarve (((_, b1) :: (r as (_, b2) :: ks)) : karta list) = b1 = b2 andalso isteBarve r
|   isteBarve _ = true;

2.3.1.1.3 Cela števila

V SML definiramo podatkovni tip number, s katerim predstavimo cela števila:

datatype number = Zero | Succ of number | Pred of number

Vrednost Zero predstavlja število 0, Succ n naslednik n ter Pred n predhodnik n. Vsako število lahko predstavimo na več načinov. Na primer, število 0 je predstavljeno z vrednostmi

Zero
Pred (Succ Zero)
Succ (Pred Zero)
Pred (Pred (Succ (Succ Zero)))
Pred (Succ (Succ (Pred Zero)))

Med vsemi je najbolj ekonomična predstavitev seveda Zero, ker ne vsebuje nepotrebnih konstruktorjev.

Sestavite funkcijo simp : number -> number, ki dano predstavitev pretvori v najbolj ekonomično, se pravi tako, ki ima najmanjše možno število konstruktorjev.

Primeri:

- simp (Pred (Succ (Succ (Pred (Pred (Succ (Pred Zero)))))));
val it = Pred Zero : number
- simp (Succ Zero);
simp (Succ Zero);
val it = Succ Zero : number

2.3.1.2 Drevesa

Binarno drevo celih števil definiramo tako:

Obstaja vozlišče Node, ki ima poleg vrednosti tudi dve poddrevesi.
Obstaja list Leaf, ki ima le vrednost.

datatype tree = Node of int * tree * tree | Leaf of int

Sprogramirajte funkciji min in max, vrneta najmanjši oz. največji element danega drevesa podatkovnega tipa tree.

2.3.2 Naloge za oddajo

V programskem jeziku SML implementirajte naslednje funkcije:

datatype number = Zero | Succ of number | Pred of number;

(* Negira število a. Pretvorba v int ni dovoljena! *)
fun neg (a : number) : number

(* Vrne vsoto števil a in b. Pretvorba v int ni dovoljena! *)
fun add (a : number, b : number) : number

(* Vrne rezultat primerjave števil a in b. Pretvorba v int ter uporaba funkcij `add` in `neg` ni dovoljena!
    namig: uporabi funkcijo simp *)
fun comp (a : number, b : number) : order

Kakšen je tip order?

datatype tree = Node of int * tree * tree | Leaf of int;

(* Vrne true, če drevo vsebuje element x. *)
fun contains (tree : tree, x : int) : bool

(* Vrne število listov v drevesu. *)
fun countLeaves (tree : tree) : int

(* Vrne število število vej v drevesu. *)
fun countBranches (tree : tree) : int

(* Vrne višino drevesa. Višina lista je 1. *)
fun height (tree : tree) : int

(* Pretvori drevo v seznam z vmesnim prehodom (in-order traversal). *)
fun toList (tree : tree) : int list

(* Vrne true, če je drevo uravnoteženo:
 * - Obe poddrevesi sta uravnoteženi.
 * - Višini poddreves se razlikujeta kvečjemu za 1.
 * - Listi so uravnoteženi po definiciji.
 *)
fun isBalanced (tree : tree) : bool

(* Vrne true, če je drevo binarno iskalno drevo:
 * - Vrednosti levega poddrevesa so strogo manjši od vrednosti vozlišča.
 * - Vrednosti desnega poddrevesa so strogo večji od vrednosti vozlišča.
 * - Obe poddrevesi sta binarni iskalni drevesi.
 * - Listi so binarna iskalna drevesa po definiciji.
 *)
fun isBST (tree : tree) : bool

Oddajte eno datoteko z imenom 02.sml.

2.4 3. laboratorijske vaje

2.4.1 Snov

2.4.1.1 Izjeme

Deklaracija izjem exception <ime izjeme> oz. exception <ime izjeme> of <ime tipa>.

exception Err;
exception Err1 of int;
exception Err2 of (int -> int);
exception Err3 of exn list;

Proženje izjem raise <ime izjeme>.
```
raise Err;
tl nil;
```

Lovljenje izjem <izraz tipa A> handle <vzorec tipa exn> => <izraz2 tipa A>

fun f x = tl x handle List.Empty => []
val a = raise Empty; (* zakaj je to narobe? *)
val a : int = raise Empty;
val a = Empty;
(raise Empty) : int;
raise Empty : int; (* zakaj je to narobe? *)
val a = (raise Empty : int) handle Empty => 1; (* zakaj je to narobe? *)
val a = raise Empty : int handle Empty => 1; (* ekvivalentno zgornjemu *)
val a = (raise Empty) : int handle Empty => 1;
(val a = 3; raise Empty) handle _ => 1; (* to ne gre, ker (val a = 3); ne gre *)
(1 div 0 handle Div => ~3) handle Empty => 3;
1 div 0 handle Div => ~3 handle Empty => 3;
1 div 0 handle izjema => case izjema of Div => ~3 | Empty => 3;
1 div 0 handle (izjema as (Div | Empty)) => case izjema of Div => ~3 | Empty => 3; (* ne reši problema *)
1 div 0 handle izjema => case izjema of Div => ~3 | Empty => 3 | _ => 1337;
(tl [] handle Div => ~3) handle Empty => 3; (* zakaj je to narobe? *)
(hd [] handle Div => ~3) handle Empty => 3; (* zakaj to ni narobe? *)
(raise Err2 (fn x => x + 1)) handle Err2 f => f 1000;
exception Err10 of 'a list; (* ne gre - "exception definitions at top level cannot contain type variables." *)

Izjeme lahko lovimo na nivoju globalnega okolja.

2.4.1.2 Polimorfizem in konstruktorji tipov

Deklaracija lastnih polimorfnih podatkovnih tipov: datatype ('<polimorfen tip1>, '<polimorfen tip2>, ...) <ime konstruktorja tipa> = <definicija tipa>

Primeri:

datatype ('prvi, 'drugi) seznamParov = Prazen | Element of 'prvi * 'drugi * ('prvi, 'drugi) seznamParov;  
type 'a multiMnozica = ('a, int) seznamParov;

Sprogramiranj funkcijo seznamParov: 'a list * 'b list -> ('a,'b) seznamParov.

- seznamParov ([1, 2, 3], ["a", "b", "c", "d"]);
val it = Element (1,"a",Element (2,"b",Element (3,"c",Prazen))) : (int,string) seznamParov

2.4.1.3 Repno-rekurzivne funkcije `map`, `foldl`, `foldr` in `filter`

Anonimne funkcije: fn <vzorec> => <telo funkcije>.

Funkcija foldl (f, z, s) vrne $f(…f(f(z,s_1),s_2),…s_n)$.
Funkcija foldr (f, z, s) vrne $f(…f(f(z,s_n),s_{n−1}),…s_1)$.
Funkcija map (f, s) vrne $[fs_1,fs_2,…fs_n]$.
Funkcija filter (f, s) vrne $[s_i∈s∣fs_i]$.

Pripadajoči tipi so:

val map = fn : ('a -> 'b) * 'a list -> 'b list
val filter = fn : ('a -> bool) * 'a list -> 'a list
val foldl = fn : ('a * 'b -> 'a) * 'a * 'b list -> 'a
val foldr = fn : ('a * 'b -> 'a) * 'a * 'b list -> 'a

Implementiraj funkcijo append : 'a list * 'a list -> 'a list (zlaganje seznamov) s foldr.

- append ([1, 2, 3], [4, 5, 6]);
val it = [1,2,3,4,5,6] : int list

2.4.1.4 Posledice uporabe repne rekurzije

Z uporabo modula Timer lahko v SML merimo čas izvajanja.

Poglejmo si, če kaj pridobimo z repno rekurzijo.

(* funkcija za izračun časa izvajanja funkcije f : unit -> 'a *)
fun timeIt f =
let val timer = Timer.startCPUTimer ()
    val _ = f ()
    val dt = Time.toMilliseconds (#usr (Timer.checkCPUTimer (timer)))
in dt end;

(* seznam s celimi števili do milijon *)
val longList = List.tabulate (1000 * 1000, (fn i => i));

(* alternirajoča vsota stevil od 0 do milijon --> 0 - 1 + 2 - 3 + 4 - ... *)
fun f1 () = foldr' (fn (z, x) => x - z, 0, longList);
fun f2 () = foldr (fn (z, x) => x - z, 0, longList); (* repno-rekurzivna različica *)

(* rezultati izvajanja *)
val rez1 = f1 ();
val rez2 = f2 ();

(* časi izvajanja v milisekundah *)
val ms1 = timeIt f1;
val ms2 = timeIt f2;

2.4.2 Naloge za oddajo

Podani so sledeči tipi:

datatype natural = Succ of natural | One;
exception NotNaturalNumber;

datatype 'a bstree = br of 'a bstree * 'a * 'a bstree | lf;
datatype direction = L | R;

V programskem jeziku SML implementirajte naslednje funkcije:

zip (x, y): Vrne seznam, ki ima na $i$-tem mestu par ($x_i,y_i$), v kateri je $x_i$ $i$-ti element seznama $x$, $y_i$ pa $i$-ti element seznama $y$. Če sta dolžini seznamov različni, vrnite pare do dolžine krajšega.
unzip: “Pseudoinverz” funkcije zip.
subtract (a, b): Vrne naravno število, ki ustreza razliki števil $a$ in $b$ ($a−b$). Če rezultat ni naravno število, proži izjemo NotNaturalNumber.
any (f, s): Vrne true, če funkcija $f$ vrne true za kateri koli element seznama $s$. Za prazen seznam naj vrne false.
map (f, s): Vrne seznam elementov, preslikanih s funkcijo $f$ vhodnega seznama $s$.
filter (f, s): Vrne seznam elementov, za katere funkcija f vrne true.
fold (f, z, s): Izračuna in vrne $f(…f(f(z,s1),s2),…sn)$.
rotate (drevo, smer): Vrne rotirano drevo v levo oz. v desno glede na smer smer (L je levo, R desno), če se to da.
rebalance: Z uporabo rotacij popravi drevo v AVL drevo z uporabo največ dveh rotacij. Poddrevesa so že AVL drevesa. V korenu se višini levega in desnega poddrevesa razlikujeta za največ dva.
avl (c, drevo, e): V AVL drevo doda element $e$, če ga še ni. Pri tem za primerjanje elementov uporabi funkcijo $c$.

Tipi pripadajočih funkcij so:

val zip = fn : 'a list * 'b list -> ('a * 'b) list
val unzip = fn : ('a * 'b) list -> 'a list * 'b list
val subtract = fn : natural * natural -> natural
val any = fn : ('a -> bool) * 'a list -> bool
val map = fn : ('a -> 'b) * 'a list -> 'b list
val filter = fn : ('a -> bool) * 'a list -> 'a list
val fold = fn : ('a * 'b -> 'a) * 'a * 'b list -> 'a
val rotate = fn : 'a bstree * direction -> 'a bstree
val rebalance = fn : 'a bstree -> 'a bstree
val avl = fn : ('a * 'a -> order) * 'a bstree * 'a -> 'a bstree

Nekaj testov za pomoč

(* izpis daljših izrazov v interpreterju *)
val _ = Control.Print.printDepth := 100;
val _ = Control.Print.printLength := 1000;
val _ = Control.Print.stringDepth := 1000;

(* izpis drevesa po nivojih *)
fun showTree (toString : 'a -> string, t : 'a bstree) =
let fun strign_of_avltree_level (lvl, t) =
   case t of  
      lf => if lvl = 0 then "nil" else "   "
      | br (l, n, r) =>
         let val make_space = String.map (fn _ => #" ")
            val sn = toString n
            val sl = strign_of_avltree_level (lvl, l)
            val sr = strign_of_avltree_level (lvl, r)
         in
            if height t = lvl
            then make_space sl ^ sn ^ make_space sr
            else sl ^ make_space sn ^ sr
         end
   fun print_levels lvl =
      if lvl >= 0
      then (print (Int.toString lvl ^ ": " ^ strign_of_avltree_level (lvl, t) ^ "\n");
         print_levels (lvl - 1))
      else ()
   in
      print_levels (height t)
   end;

(* primeri vstavljanja elementov v AVL drevo *)
fun avlInt (t, i) = avl (Int.compare, t, i);
fun showTreeInt t = showTree(Int.toString, t);

val tr = lf : int bstree;
val _ = showTreeInt tr;
val tr = avlInt (tr, 1);
val _ = showTreeInt tr;
val tr = avlInt (tr, 2);
val _ = showTreeInt tr;
val tr = avlInt (tr, 3);
val _ = showTreeInt tr;
val tr = avlInt (tr, 4);
val _ = showTreeInt tr;
val tr = avlInt (tr, 5);
val _ = showTreeInt tr;
val tr = avlInt (tr, 6);
val _ = showTreeInt tr;
val tr = avlInt (tr, 7);
val _ = showTreeInt tr;
val tr = avlInt (tr, ~4);
val _ = showTreeInt tr;
val tr = avlInt (tr, ~3);
val _ = showTreeInt tr;
val tr = avlInt (tr, ~2);
val _ = showTreeInt tr;
val tr = avlInt (tr, ~1);
val _ = showTreeInt tr;
val tr = avlInt (tr, 0);
val _ = showTreeInt tr;

val from0to13 = fold (fn (z, x) => avl (Int.compare, z, x), lf, List.tabulate (14, fn i => i));

2.5 4. laboratorijske vaje

2.5.1 Snov

2.5.1.1 Currying

$(A \rightarrow (B \rightarrow C)) = (A \rightarrow B \rightarrow C) \neq ((A \rightarrow B) \rightarrow C)$
$((A \times B) \rightarrow C) = (A \times B \rightarrow C)$
$f \; x \; y = (f(x))(y)$

V SML implementiraj naslednje funkcije podane z njihovimi domenami, kodomenami in predpisi. Kaj so njihove funkcionalnosti?

$f : Z \rightarrow (Z \rightarrow Z)$
s predpisom $(x \mapsto (y \mapsto xy))$
$\text{curry} : (A \times B \rightarrow C) \rightarrow (A \rightarrow (B \rightarrow C))$
s predpisom $(f \mapsto (x \mapsto (y \mapsto f(x,y))))$
$\text{uncurry} = \text{curry}^{-1} : (A \rightarrow (B \rightarrow C)) \rightarrow (A \times B \rightarrow C)$
s predpisom $(f \mapsto ((x,y) \mapsto (f \; x \; y)))$
$\text{swap} : (A \rightarrow (B \rightarrow C)) \rightarrow (B \rightarrow (A \rightarrow C))$
s predpisom $(f \mapsto (x \mapsto (y \mapsto (f \; y \; x))))$
$\text{compose} : (A \rightarrow B) \times (C \rightarrow A) \rightarrow (C \rightarrow B)$
s predpisom $((f,g) \mapsto (x \mapsto f(g(x))))$
$\text{compose2} : (A \rightarrow B) \rightarrow (C \rightarrow A) \rightarrow (C \rightarrow B)$
s predpisom $(f \mapsto (g \mapsto (x \mapsto f(g(x)))))$
$\text{apply} : (A \rightarrow B) \times A \rightarrow B$
s predpisom $((f,x) \mapsto f(x))$
$\text{apply2} : ((A \rightarrow B) \rightarrow A) \rightarrow B$
s predpisom $(f \mapsto (x \mapsto f(x)))$
$\text{fold1} : (A \times B \rightarrow B) \rightarrow B \rightarrow A^n \rightarrow B$
s predpisom $(f \mapsto (z \mapsto (x \mapsto f(x_n, \ldots, f(x_2, f(x_1,z)) \ldots ))))$
$\text{fold12} : (A \rightarrow B \rightarrow B) \rightarrow B \rightarrow A^n \rightarrow B$
s predpisom $(f \mapsto (z \mapsto (x \mapsto f \; x_n \; (\ldots (f \; x_2 \; (f \; x_1 \; z)) \ldots )))$
$\text{foldr} : (A \times B \rightarrow B) \rightarrow B \rightarrow A^n \rightarrow B$
s predpisom $(f \mapsto (z \mapsto (x \mapsto f(x_1, \ldots, f(x_{n-1}, f(x_n,z)) \ldots ))))$
$\text{foldr2} : (A \rightarrow B \rightarrow B) \rightarrow B \rightarrow A^n \rightarrow B$
s predpisom $(f \mapsto (z \mapsto (x \mapsto f \; x_1 \; (\ldots (f \; x_{n-1} \; (f \; x_n \; z)) \ldots ))))$
$\text{map} : (A \rightarrow B) \rightarrow A^n \rightarrow B^n$
s predpisom $(f \mapsto (x \mapsto [f(x_1), f(x_2), \ldots f(x_n)]))$
$\text{iterate} : (\mathbb{N} \rightarrow (A \rightarrow A)) \rightarrow (A \rightarrow A))$
s predpisom $(n \mapsto (f \mapsto f^n))$
$D : (\mathbb{R} \rightarrow \mathbb{R}) \rightarrow (\mathbb{R} \rightarrow \mathbb{R})$
s predpisom $(f \mapsto f')$
$D^n : \mathbb{N} \rightarrow (\mathbb{R} \rightarrow \mathbb{R}) \rightarrow (\mathbb{R} \rightarrow \mathbb{R})$
s predpisom $(n \mapsto (f \mapsto f^{(n)}))$
$\text{gradient} : (\mathbb{R}^n \rightarrow \mathbb{R}) \rightarrow (\mathbb{R}^n \rightarrow \mathbb{R}^n)$
s predpisom $(f \mapsto (x \mapsto [D_{x_1}f, D_{x_2}f, \ldots D_{x_n}f]^T))$, gradient
$\text{laplacian} : (\mathbb{R}^n \rightarrow \mathbb{R}) \rightarrow (\mathbb{R}^n \rightarrow \mathbb{R})$
s predpisom $(f \mapsto (x \mapsto \sum_i D_{xi}^2f))$, Laplace operator

rešitve

val _ = Control.polyEqWarn := false;

val f : int -> (int -> int) = fn x => (fn y => x * y);
fun f x = fn y => x * y;
fun f x y = x * y;

val curry : ('a * 'b -> 'c) -> 'a -> 'b -> 'c =
   fn f => fn x => fn y => f (x, y);
fun curry (f : 'a * 'b -> 'c) = fn x => fn y => f (x, y);
fun curry f x y = f (x, y);
(* val addc = curry Int.+; *)

val uncurry = fn f => fn (x, y) => f x y;
fun uncurry f = fn (x, y) => f x y;
fun uncurry f (x, y) = f x y;
(* val id1 = fn x => curry (uncurry x); *)
(* val id2 = fn x => uncurry (curry x); *)

val swap = fn f => fn x => fn y => f y x;
fun swap f x y = f y x;

val compose = fn (f, g) => fn x => f (g x);
fun compose (f, g) x = f (g x);
(*infix 3 o*)
val compose = op o;
fun compose (f, g) x = (f o g) x;
fun compose (f, g) = f o g;
val compose = General.o;
val compose = op o;

val compose2 = fn f => fn g => fn x => f (g x);
fun compose2 f g = f o g;

val apply = fn (f, x) => f x;
fun apply (f, x) = f x;
infixr 2 $;
fun f $ x = f x;
fun op$ (f, x) = f x; 
(* f (g (h x)) = f $ g $ h $ x = f $ g $ h x *)
fun compose (f, g) x = f $ g x;

val apply2 = fn f => fn x => f x;
fun apply2 f x = f x;
fun apply2 f = f;

fun foldl _ acc [] = acc
|   foldl f acc (x :: xs) = foldl f (f (x, acc)) xs;
val foldl = List.foldl;

fun foldl2 _ acc [] = acc
|   foldl2 f acc (x :: xs) = foldl2 f (f x acc) xs;
fun foldl2 f acc xs = List.foldl (uncurry f) acc xs;
fun foldl2 f = List.foldl (uncurry f);
fun foldl2 f = List.foldl $ uncurry f;

fun rev xs = List.foldl (fn (x, acc) => x :: acc) [] xs;
fun rev xs = List.foldl List.:: [] xs;
val rev = List.rev;

fun foldr f acc xs = List.foldl f acc (List.rev xs);
fun foldr f acc xs = List.foldl f acc o List.rev;
val foldr = List.foldr;

fun foldr2 f = List.foldr $ uncurry f;

fun map _ [] = []
|   map f (x :: xs) = f x :: map f xs;
fun map f = List.foldr (fn (x, acc) => f x :: acc) [];
val map = List.map;

fun filter _ [] = []
|   filter f (x :: xs) = if f x then x :: filter f xs else filter f xs;
fun filter f = List.foldr (fn (x, acc) => if f x then x :: acc else acc) [];
val filter = List.filter;

fun eq a b = a = b;
fun neq a b = a <> b;

fun remove a xs = List.filter (fn x => a <> x) xs;
fun remove a xs = List.filter (neq a) xs;
fun remove a = List.filter (not o eq a);

fun iterate 0 f = (fn x => x)
|   iterate n f = f o (iterate (n - 1) f);

fun sq x = x * x;
(* (iterate 0 sq) 3; *)
(* (iterate 1 sq) 3; *)
(* (iterate 2 sq) 3; *)

fun D f = fn x => let val h = 1E~5 in (f (x + h) - f (x - h)) / (2.0 * h) end;
(* (D (fn x => 2.0 * x + 1.0)) 3.0; *)
(* D Math.sin Math.pi; *)

fun Dn n = iterate n D;
(* Dn 0 Math.sin (Math.pi/6.0); *)
(* Dn 1 Math.sin (Math.pi/6.0); *)
(* Dn 2 Math.sin (Math.pi/6.0); *)
(* Dn 3 Math.sin (Math.pi/6.0); *)

fun partial i f p = D (fn xi => f $ Vector.update (p, i, xi)) $ Vector.sub (p, i);
(* exception Domian;
fun f #[x, y] : real = x * x - y * y
|   f _ = raise Domain; *)
(* partial 0 f #[0.0, 0.0];
partial 1 f #[0.0, 1.0];
partial 1 f #[1.0, 0.0];
partial 0 f #[4.0, 3.0]; *)

fun gradient f p = Vector.tabulate (Vector.length p, fn i => partial i f p);
(* grad(x^2 - y^2) = (2 x, -2 y) *)
(* gradient f #[0.0, 0.0];
gradient f #[0.0, 1.0];
gradient f #[1.0, 0.0];
gradient f #[4.0, 3.0]; *)


(* fun laplacian f p = Vector.foldl Real.+ 0.0 (Vector.tabulate (Vector.length p,
   fn i => (D o D) (fn xi => f $ Vector.update (p, i, xi)) $ Vector.sub (p, i))); *)
fun laplacian f p = Vector.foldl Real.+ 0.0
   (Vector.tabulate (Vector.length p, fn i => (partial i o partial i) f p));
(* Δ(x^2 - y^2) = 0 *)
(* laplacian f #[0.0, 0.0];
laplacian f #[0.0, 1.0];
laplacian f #[1.0, 0.0];
laplacian f #[4.0, 3.0]; *)

2.5.1.2 KRATEK in DOLGI zapis funkcij

dolgi zapis val <ime fun.> = fn x => fn y ... => <telo fun.>
dolgi zapis (rekurzivne funkcije) val rec <ime fun.> = fn x => fn y ... => <telo fun.>
kratek zapis fun <ime fun.> x y ... = <telo fun.>

2.5.1.3 Zaporedje izrazov

Zaporedje izrazov je izraz, ki ima naslednjo obliko (<izraz 1> ; <izraz 2> ; ... ; <izraz n>). Njena vrednost je vrednost zadnjega izraza.
(Pazi! Vezava spremenljivk, deklaracija funkcij, … niso izrazi)

Primer.

- (3 ; "aaa" ; fn x => x + 1) 5;
val it = 6 : int

2.5.1.4 Primerljivi tipi

Primerljive tipe za razliko od neprimerljivih (real, 'a * real, 'a -> 'b, …) lahko primerjamo ali predstavljajo isto vrednost z operatorjem op = : ''a * ''a -> bool. Najsplošnejši tak tip je ''a, ki je nadtip vsem preostalim primerljivim tipom.

- {a = 1, b = 2} = {b = 2, a = 1};
val it = true : bool

- [1, 3] = [3, 1];
val it = false : bool

- (fn x => x + 1) = (fn x => x + 1); (* Kako težek je ta problem? *)
(* Error: operator and operand do not agree [equality type required] *)

Še vedno pa lahko programer sam definira funkcijo za pripenjanje za poljuben tip!

2.5.2 Naloge za oddajo

V programskem jeziku SML implementirajte naslednje funkcije brez uporabe pomožnih funkcij. Uporabite lahko anonimne funkcije ter strukture List, ListPair, Math, String in Int.

(* Podan seznam xs agregira z začetno vrednostjo z in funkcijo f v vrednost f (f (f z s_1) s_2) s_3) ... *)
(* Aggregates xs with an initial value z and function f and returns f (f (f z s_1) s_2) s_3) ... *)
val reduce = fn : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a

(* Vrne seznam, ki vsebuje kvadrate števil iz vhodnega seznama. Uporabite List.map. *)
(* Returns a list of squares of the numbers. Use List.map. *)
val squares = fn : int list -> int list

(* Vrne seznam, ki vsebuje vsa soda števila iz vhodnega seznama. Uporabite List.filter. *)
(* Returns a list that contains only even numbers from xs. Use List.filter. *)
val onlyEven = fn : int list -> int list

(* Vrne najboljši niz glede na funkcijo f (prvi arg.). Funkcija f primerja dva niza in vrne true, če je prvi niz boljši od drugega. Uporabite List.foldl. Najboljši niz v praznem seznamu je prazen niz. *)
(* Returns the best string according to the function f (first arg.). The function f compares two strings and returns true if the first string is better than the other. Use List.foldl. The best string in an empty list is an empty string. *)
val bestString = fn : (string * string -> bool) -> string list -> string

(* Vrne leksikografsko največji niz. Uporabite bestString. *)
(* Returns the largest string according to alphabetical ordering. Use bestString. *)
val largestString = fn : string list -> string

(* Vrne najdaljši niz. Uporabite bestString. *)
(* Returns the longest string. Use bestString. *)
val longestString = fn : string list -> string

(* Seznam uredi naraščajoče z algoritmom quicksort. Prvi argument je funkcija za primerjanje. *)
(* Sorts the list with quicksort. First argument is a compare function. *)
val quicksort = fn : ('a * 'a -> order) -> 'a list -> 'a list

(* Vrne skalarni produkt dveh vektorjev. Uporabite List.foldl in ListPair.map. *)
(* Returns the scalar product of two vectors. Use List.foldl and ListPair.map. *)
val dot = fn : int list -> int list -> int

(* Vrne transponirano matriko. Matrika je podana z vrstičnimi vektorji od zgoraj navzdol:
  [[1,2,3],[4,5,6],[7,8,9]] predstavlja matriko
   [ 1 2 3 ]
   [ 4 5 6 ]
   [ 7 8 9 ]
*)
(* Returns the transpose of m. The matrix m is given with row vectors from top to bottom:
  [[1,2,3],[4,5,6],[7,8,9]] represents the matrix
   [ 1 2 3 ]
   [ 4 5 6 ]
   [ 7 8 9 ]
*)
val transpose = fn : 'a list list -> 'a list list

(* Zmnoži dve matriki. Uporabite dot in transpose. *)
(* Multiplies two matrices. Use dot and transpose. *)
val multiply = fn : int list list -> int list list -> int list list

(* V podanem seznamu prešteje zaporedne enake elemente in vrne seznam parov (vrednost, število ponovitev). Podobno deluje UNIX-ovo orodje
   uniq -c. *)
(* Counts successive equal elements and returns a list of pairs (value, count). The unix tool uniq -c works similarly. *)
val group = fn : ''a list -> (''a * int) list

(* Elemente iz podanega seznama razvrsti v ekvivalenčne razrede. Znotraj razredov naj bodo elementi v istem vrstnem redu kot v podanem seznamu. Ekvivalentnost elementov definira funkcija f, ki za dva elementa vrne true, če sta ekvivalentna. *)
(* Sorts the elements from a list into equivalence classes. The order of elements inside each equivalence class should be the same as in the original list. The equivalence relation is given with a function f, which returns true, if two elements are equivalent. *)
val equivalenceClasses = fn : ('a -> 'a -> bool) -> 'a list -> 'a list list

Oddajte eno datoteko z imenom 04.sml.

2.6 5. laboratorijske vaje

2.6.1 Snov

2.6.1.1 Tip `unit`

Je primerljiv tip, s katerim lahko predstavimo le eno vrednost (). Nanjo lahko gledamo kot na prazno terko.

“terka” z dvema elementoma (a, b) oz. {1=a, 2=b}
“terka” z enim elementom {1=a} (zapis oklepaji ne gre — (a))
“terka” z nič elementi () oz. {}

Funkcija print : string -> unit izpiše na standardni izhod podani niz, vrednost samega izraza njene aplikacije je (). V SML funkcije vedno vračajo neko vrednost. Poleg tega vedno sprejema natanko en argument.

Zapis f () ne pomeni “klic” (aplikacija) funkcije z nič argumenti ampak za enim samim (), ki je tipa unit.

Funkcije v povezavi z tipom unit:

ignore : ’a -> unit: funkcija sprejme karkoli in vrne ()
before : ’a * unit -> ’a: in-fiksni “operator”, ki ignorira desno stran (izraz na desni more biti tipa unit).

Primer
```
- 3 before print "a\n" before print "b\n" before print "c\n";
a
b
c
val it = 3 : int
```

2.6.1.2 Mutacije

Mutacije so tipa 'a ref.

ustvarjanje reference, funkcija ref : 'a -> 'a ref
dereferenciranje, operator ! : 'a ref -> 'a
prirejanje, in-fiksni operator := 'a ref * a -> unit

- val a = ref [1];
val a = ref [1] : int list ref

- fun f x = x :: !a;
val f = fn : int -> int list

- f 3;
val it = [3,1] : int list

- a := [];
val it = () : unit

- f 3;
val it = [3] : int list


- fun faktoriela n =
    let
      val n = ref n
      val i = ref 1
    in
      while !n > 0 do (i := !i * !n; n := !n - 1);
      !i
    end;

- faktoriela 10;
val it = 3628800 : int

“Mutacije niso rekurzivne!” (int list ref $\neq$ int ref list ref)

2.6.1.3 Mutirani seznami

Implementiraj funkcijo val bubbleSort = fn : int array -> unit. Funkcija sprejme mutacijo int array, glej modul Array. Njena funkcionalnost je sortiranje podane table z uporabo algoritma BubbleSort. Pomagaj si z rezervirano besedo while.

rešitve

fun swap (a, i, j) =
   let val temp = Array.sub (a, i)
   in (Array.update (a, i, Array.sub (a, j)); Array.update (a, j, temp)) end;

fun bubbleSort a =
   let val n = ref (Array.length a)
      val i = ref 0
      val swapped = ref true
   in
   while (!swapped) do (
      swapped := false;
      i := 1;
      while (!i < !n) do (
            (if Array.sub (a, !i - 1) > Array.sub (a, !i)
            then (swap (a, !i - 1, !i);
               swapped := true)
            else ()); i := !i + 1))
   end;

val sez = Array.fromList [5, 2, ~3, 1, 0, 4];
bubbleSort sez;
sez;

2.6.1.4 Zanka `while`

Spodnja programa sta si med seboj ekvivalentna.

val n = ref 10;
val i = ref 0;

while (!n > 0) do
    (i := !i + !n; n := !n-1);
(* n = 0, i = 55 *)

val n = ref 10;
val i = ref 0;

let fun myWhile () =
    if (!n > 0)
    then (i := !i + !n; n := !n-1; myWhile ())
    else ()
in myWhile () end;
(* n = 0, i = 55 *)

2.6.1.5 Moduli

Primer modula za delo s kompleksnimi števili.

signature COMPLEX =
sig
    type complex

    val complex : Real.real -> Real.real -> complex
    val i : complex
    val re : complex -> Real.real
    val im : complex -> Real.real

    val neg : complex -> complex
    val inv : complex -> complex

    val * : complex * complex -> complex
    val + : complex * complex -> complex

    val toString: complex -> String.string
end;

Implementacija modula Complex

structure Complex :> COMPLEX =
struct
    type complex = Real.real * Real.real

    fun complex a b = (a, b)

    val i : complex = (0.0, 1.0)
    fun re ((a, b) : complex) = a
    fun im ((a, b) : complex) = b

    fun neg ((a, b) : complex) = let open Real in (~ a, ~ b) end
    fun inv ((a, b) : complex) = let open Real val s = a * a + b * b in (a / s, ~ b / s) end

    fun conj ((a, b) : complex) = (a, Real.~ b)

    fun op* ((a1, b1) : complex, (a2, b2) : complex) = let open Real in (a1 * a2 - b1 * b2, a1 * b2 + a2 * b1) end
    fun op+ ((a1, b1) : complex, (a2, b2) : complex) = let open Real in (a1 + a2, b1 + b2) end

    fun toString ((a, b) : complex) = Real.toString a ^ " + " ^ Real.toString b ^ "i"
end;

2.6.1.6 Dodatki

open <ime strukture> elemente strukture da v globalno (lokalno) okolje.
local <lokalne definicije> in <uporaba le teh> end lokalni del strukture

2.6.1.7 Funktorji

Primer funktorja za zgoščene množice. SML implementacijo najdete tukaj.

signature KEY =
sig
    type key
    val sameKey : key -> key -> bool
end;

signature SET =
sig
    structure Key : KEY
    type item
    type set
    val mkEmpty : unit -> set
    val toList : set -> item list
    val add : set -> item -> unit
    val subtract : set -> item -> unit
    val member : set -> item -> bool
    val isEmpty : set -> bool
    val fold : (item * 'b -> 'b) -> 'b -> set -> 'b
end;



functor ListSetFn (K : KEY) : SET where type item = K.key =
struct
    structure Key = K
    type item = K.key
    type set = item list ref
    fun mkEmpty () : set = ref []
    fun toList s = !s
    fun member s e = List.exists (K.sameKey e) (!s)
    fun add s e = if member s e then () else (s := e :: !s)
    fun subtract s e = s := (List.filter (not o K.sameKey e) (!s))
    fun isEmpty s = null (!s)
    fun fold f z s = List.foldl f z (!s)
end;


structure ListSetSet = ListSetFn (type key = int fun sameKey x y = x = y)

2.6.1.8 Funktorji + curying

signature MONOID =
sig
    type t
    val e : t
    val + : t * t -> t
end;

signature GROUP =
sig
    type t
    val e : t
    val * : t * t -> t
    val inv : t -> t
end;

signature RING =
sig
    type t
    val + : t * t -> t
    val zero : t
    val neg : t -> t
    val * : t * t -> t
    val one : t
end;

S pomočjo naslednjega funktorja lahko grupo G in mondid M združimo v kolobar.

(* funsig MKRING (structure G: GROUP structure M: MONOID where type t = G.t) = RING *)
functor MakeRing (G: GROUP) (M: MONOID where type t = G.t) : RING =
struct
    type t = G.t
    fun op+ (a, b) = G.* (a, b)
    val zero = G.e
    fun neg a = G.inv a
    fun op* (a, b) = M.+ (a, b)
    val one = M.e
end

structure Z13 : GROUP =
struct
    type t = int;
    val e = 0;
    fun op * (a, b) =  (a + b mod 13);
    fun inv a = ~a mod 13;
end;

structure Zm13 : MONOID =
struct
    type t = int;
    val e = 1;
    fun op + (a, b) =  (a * b mod 13);
end;

(* delno apliciran funktor *)
functor MakeRingP = MakeRing (Z13)

structure Z = Zm13;
structure R13 = MakeRing (Z13) (Zm13)
structure R13 = MakeRingP (Zm13)

2.6.2 Naloge za oddajo

(NE SPREMNINJAJTE PODPISOV!)

2.6.2.1 Modul `Rational`

V programskem jeziku SML implementirajte naslednji modul (programski vmesnik) za delo z racionalnimi števili. Vaša struktura naj se imenuje Rational in naj definira podatkovni tip (datatype) rational (ki je lahko bodisi celo število bodisi ulomek).

Ulomki naj sledijo naslednjim pravilom:

Imenovalec je vedno strogo večji od 1.
Vsak ulomek je okrajšan.

V oddani datoteki implementirajte le strukturo Rational, ki ustreza podpisu RATIONAL. Modul naj ne bo popisan, dana datoteka pa popisa ne vsebuje.

signature RATIONAL =
sig
    (* Definirajte podatkovni tip rational, ki podpira preverjanje enakosti. *)
    eqtype rational

    (* Definirajte izjemo, ki se kliče pri delu z neveljavnimi ulomki - deljenju z nič. *)
    exception BadRational

    (* Vrne racionalno število, ki je rezultat deljenja dveh podanih celih števil. *)
    val makeRational: int * int -> rational

    (* Vrne nasprotno vrednost podanega števila. *)
    val neg: rational -> rational

    (* Vrne obratno vrednost podanega števila. *)
    val inv: rational -> rational

    (* Funkcije za seštevanje in množenje. Rezultat vsake operacije naj sledi postavljenim pravilom. *)
    val add: rational * rational -> rational
    val mul: rational * rational -> rational

    (* Vrne niz, ki ustreza podanemu številu.
        Če je število celo, naj vrne niz oblike "x" oz. "~x".
        Če je število ulomek, naj vrne niz oblike "x/y" oz. "~x/y". *)
    val toString: rational -> string
end

Primeri.

structure Rational : RATIONAL
- structure Rational :> RATIONAL = Rational;
structure Rational : RATIONAL
- open Rational;
opening Rational
  eqtype rational
  exception BadRational
  val makeRational : int * int -> rational
  val neg : rational -> rational
  val inv : rational -> rational
  val add : rational * rational -> rational
  val mul : rational * rational -> rational
  val toString : rational -> string
- val r = add (makeRational (14, ~12),  makeRational (6, 10));
val r = - : rational
- toString r;
val it = "~17/30" : string

2.6.2.2 Funktor `SetFn`

Implementirajte tudi funktor SetFn, ki ustreza podpisu SETFN. Funktor vrača modul, ki je podpisan s podpisom SET, ki ima razkrito definicijo podatkovnega tipa type.

signature EQ =
sig
    type t
    val eq : t -> t -> bool
end

signature SET =
sig
    (* podatkovni tip za elemente množice *)
    type item

    (* podatkovni tip množico *)
    type set

    (* prazna množica *)
    val empty : set

    (* vrne množico s samo podanim elementom *)
    val singleton : item -> set

    (* unija množic *)
    val union : set -> set -> set

    (* razlika množic (prva - druga) *)
    val difference : set -> set -> set

    (* a je prva množica podmnožica druge *)
    val subset : set -> set -> bool
end

funsig SETFN (Eq : EQ) = SET

Primeri.

- functor SetFn : SETFN = SetFn;
functor SetFn(Eq: sig
                    type t
                    val eq : t -> t -> bool
                  end) :
             sig
               type item
               type set
               val empty : set
               val singleton : item -> set
               val union : set -> set -> set
               val difference : set -> set -> set
               val subset : set -> set -> bool
             end
- structure S = SetFn (type t = int fun eq x y = x = y);
structure S : SET
- S.empty;
val it = - : S.set
- S.singleton;
val it = fn : S.item -> S.set
- val s3 = S.singleton 3;
val s3 = - : S.set
- val s4 = S.singleton 4;
val s4 = - : S.set
- S.subset s4 (S.union s3 s4);
val it = true : bool

Če pozenete rešeno nalogo skozi iterpreter dobite (oz. nekaj podobnega):

[opening 05.sml]
[autoloading]
[library $SMLNJ-BASIS/basis.cm is stable]
[library $SMLNJ-BASIS/(basis.cm):basis-common.cm is stable]
[autoloading done]
structure Rational :
  sig
    datatype rational = Frac of int * int | Whole of int
    exception BadRational
    val makeRational : int * int -> rational
    val neg : rational -> rational
    val inv : rational -> rational
    val add : rational * rational -> rational
    val mul : rational * rational -> rational
    val toString : rational -> string
  end
signature EQ =
  sig
    type t
    val eq : t -> t -> bool
  end
signature SET =
  sig
    type item
    type set
    val empty : set
    val singleton : item -> set
    val union : set -> set -> set
    val difference : set -> set -> set
    val subset : set -> set -> bool
  end
[autoloading]
[autoloading done]
functor SetFn(Eq: sig
                    type t
                    val eq : t -> t -> bool
                  end) :
             sig
               type item = Eq.t
               type set
               val empty : set
               val singleton : item -> set
               val union : set -> set -> set
               val difference : set -> set -> set
               val subset : set -> set -> bool
             end

Oddajte eno datoteko z imenom 05.sml.

2.7 6. laboratorijske vaje

2.7.1 Snov

2.7.1.1 Racket

Racket + DrRacket: archlinux pacman -S racket, ostali OS
Dokumentacija
vezava spremenljivk/funkcij (define ime izraz)
anonimne funkcije (lambda (argumenti) izraz) ali (λ (argumenti) izraz)
funkcije (define (ime argumenti) izraz)
funkcije (define ((ime arg1) arg2 ...) izraz)
terke '(prvi drugi . zadnji) (cons glava rep)
seznami '(prvi drugi zadnji) (cons glava rep) (list prvi drugi zadnji) (cons prvi (cons drugi (cons zadnji null)))
prazen seznam null '()
delo s seznami null? first rest cons
sestevanje, odštevanje … (+ a b c ...)
agregiranje (foldl funcija zacetna-vrenost seznam), podobno tudi map in filter
“pametna” aplikacija (apply funkcija seznam)
izpis na zaslon
lokalno okolje (let ([ime izraz] ...) uporaba-okolja),
“razširjeno” lokalno okolje (let* ([ime izraz] ...) uporaba-okolja), podobno tudi letrec.

2.7.1.2 Priprava testov

Vnosi v testni datoteki program-tests.rkt:

Način 1:

(display "<ime testa>")
(displayln (equal?
      (ime-funkcije argumenti)
      pricakovan-rezultat))

Način 2: glej Racket dokumentacijo.

Testiranje: (load program.rkt) (load program-tests.rkt).

2.7.1.3 Bližnjice v DrRacket

Autocomplete: ctrl + /
Poravnava: ctrl + i
“Run”: ctrl-r
Nastavitve: Edit -> Keybindings
Primer nastavitev: (ctrl + a : Run in ctrl + w : delete word) v datoteki key-bindings.rkt.
Dokumentacijo za bližnjice dobite tukaj.

V interpreterju:

Navigacija po zgodovini: ctrl + ↑, ctrl + ↓
Skoči na konec: ↓
Interpretiraj vnešen izraz: ctrl + enter

2.7.2 Naloge

2.7.2.1 Naloga na vajah

Uvodni primeri (brez rešitev).

2.7.2.2 Naloge za oddajo

V programskem jeziku Racket implementirajte naslednje funkcije:

power, ki sprejme število x in potenco n, ter vrne n-to potenco števila x (0 je veljavna potenca).
```
> (power 2 3)
8
```
gcd, ki sprejme dve števili, in vrne njun največji skupni delitelj.
```
> (gcd 7 3)
1
```
fib, ki sprejme število n in vrne n-to Fibonaccijevo število.
```
> (fib 3)
2
```
reverse, ki sprejme seznam in vrne obrnjen seznam (za dodajanje na konec seznama lahko uporabite vgrajeno funkcijo append).
```
> (reverse (list 1 2 3))
'(3 2 1)
```
remove, ki sprejme element x in seznam, ter vrne nov seznam, ki je enak kot vhodni, le da so v njem odstranjene vse pojavitve elementa x.
```
> (remove 3 (list 1 2 3 4 5 4 3 2 1))
'(1 2 4 5 4 2 1)
```
map, ki sprejme funkcijo in seznam ter vrne seznam rezultatov, ki jih vrne podana funkcija, če jo zapovrstjo kličemo na elementih vhodnega seznama.
```
> (map (lambda (a) (* a 2)) (list 1 2 3))
'(2 4 6)
```
filter, ki sprejme funkcijo in seznam ter vrne seznam, ki vsebuje vse elemente vhodnega seznama, za katere podana funkcija vrne resnično vrednost.
```
> (filter (lambda (a) (= (modulo a 2) 0)) (list 1 2 3))
'(2)
```
zip, ki sprejme dva seznama, vrne pa seznam parov, ki je tako dolg, kot krajši izmed vhodnih seznamov. Prvi element izhodnega seznama vsebuje par prvih števil vhodnih seznamov, drugi element par drugih števil, …
```
> (zip (list 1 2 3) (list 4 5 6))
'((1 . 4) (2 . 5) (3 . 6))
```
range, ki sprejme tri števila, začetek, konec in korak. Vrne seznam števil, ki se začne s številom začetek, vsako naslednje število pa je za korak večje od prejšnjega. Največje število v seznamu je manjše ali enako od števila konec. Korak bo vedno pozitiven, konec pa vedno večji od začetka.
```
> (range 1 3 1)
'(1 2 3)
```
is-palindrome, ki sprejme seznam ter vrne true, če je seznam palindrom in false v nasprotnem primeru.
```
> (is-palindrome (list 2 3 5 1 6 1 5 3 2))
#t
```

Rešitve nalog shranite v eno datoteko z imenom 06.rkt in jo oddajte na učilnici.

2.8 7. laboratorijske vaje

2.8.1 Naloge za oddajo

2.8.1.1 Naloge na vajah

naloge

2.8.1.2 Naloge za oddajo

V programskem jeziku Racket implementirajte naslednje funkcije:

tok ones, ki ustreza zaporedju samih enic (1 1 1 ...)

> (car ones)
1
> (car ((cdr ((cdr ones)))))
1

tok naturals, ki ustreza zaporedju naravnih števil (1 2 3 4 ...)
```
> (car naturals)
1
> (car ((cdr ((cdr naturals)))))
3
```
tok fibs, ki ustreza zaporedju Fibonaccijevih števil (1 1 2 3 5 ...)
```
> (car ((cdr ((cdr fibs)))))
2
```
first, ki sprejme število n in tok, ter vrne seznam prvih n števil iz toka.
```
> (first 5 fibs)
'(1 1 2 3 5)
```
squares, ki sprejme tok, in vrne nov tok, ki vsebuje kvadrirane elemente prvega toka.
```
> (first 5 (squares fibs))
'(1 1 4 9 25)
```
makro sml, ki podpira uporabo “SML sintakse” za delo s seznami. Podprite SML funkcije/konstruktorje ::, hd, tl, null in nil. Sintaksa naj bo taka, kot je navedena v primeru uporabe spodaj. (Sintaksa seveda ne bo povsem enaka SML-jevi, saj zaradi zahtev Racketa še vedno ne smemo pisati odvečnih oklepajev, potrebno pa je pisati presledke okoli funkcij/parametrov, pa vseeno.)
```
> (sml nil)
'()
> (sml null (sml nil))
#t
> (sml hd (sml 5 :: null))
5
> (sml tl (sml 5 :: (sml 4 :: (sml nil))))
'(4)
```
my-delay, my-force. Funkciji za zakasnitev in sprožitev delujeta tako, da si funkcija za sprožitev pri prvem klicu zapomni rezultat, ob naslednjih pa vrne shranjeno vrednost. Popravite funkciji tako, da bo funkcija za sprožitev ob prvem in nato ob vsakem petem klicu ponovno izračunala in shranila rezultat.
```
> (define f (my-delay (lambda () (begin (write "bla") 123))))
> (my-force f)
"bla"123
> (my-force f)
123
> (my-force f)
123
> (my-force f)
123
> (my-force f)
123
> (my-force f)
"bla"123
> (my-force f)
123
```
partitions, ki sprejme števili k in n, ter vrne število različnih načinov, na katere lahko n zapišemo kot vsoto k naravnih števil (naravna števila se v tem kontekstu začnejo z 1). (Če se dva zapisa razlikujeta samo v vrstnem redu elementov vsote, ju obravnavamo kot en sam zapis. https://en.wikipedia.org/wiki/Partition_(number_theory))
```
> (partitions 3 7)
4
```

Rešitve nalog shranite v eno datoteko z imenom 07.rkt in jo oddajte na učilnici.

2.9 8. laboratorijske vaje

2.9.1 Naloge za oddajo

2.9.1.1 FRInterpreter 0.1

Implementirajte interpreter oz. funkcijo fri, ki sprejme izraz v interpretiranem programskem jeziku FR. Vrne vrednost, v katero se evalvira podani izraz, glede na spodaj definirane elemente jezika. Delovanje v primeru neveljavnega izraza ni definirano (praktično pa je, če v tem primeru interpreter proži izjemo).

Z uporabo lastnih podatkovnih tipov (struct) implementirajte naslednje elemente jezika. Vsi uporabljeni podatkovni tipi naj uporabljajo #:transparent.

2.9.1.2 Podatkovni tipi

cela stevila (int n), kjer je n celo število v jeziku Racket.
```
> (fri (int 5))
(int 5)
```
logični vrednosti (true) in (false), kjer (true) predstavlja resnično vrednost, (false) pa neresnično.
```
> (fri (false))
(false)
```

2.9.1.3 Nadzor toka

aritmetično-logične operacije
- “seštevanje” (add e1 e2): Glede na tipe argumentov ločimo več primerov:
  - Če sta izraza logični vrednosti je rezultat disjunkcija (e1 ali e2).
  - Če sta izraza e1 in e2 celi števili, potem je rezultat njuna vsota.
```
> (fri (add (int 3) (int 2)))
(int 5)

> (fri (add (false) (true)))
(true)
```
- “množenje” (mul e1 e2): Glede na tipe argumentov ločimo več primerov:
  - Če sta izraza logični vrednosti je rezultat konjunkcija (e1 in e2).
  - Če sta izraza e1 in e2 celi števili, potem je rezultat njun produkt.
```
> (fri (mul (int 3) (int 2)))
(int 6)

> (fri (mul (false) (true)))
(false)
```
- primerjanje (?leq e1 e2): Rezultat je logična vrednost v FR. Glede na tipe argumentov ločimo več primerov:
  - Če sta izraza logični vrednosti je rezultat implikacija (iz e1 sledi e2).
  - Če sta izraza e1 in e2 celi števili, potem je rezultat e1 ≤ e2.
```
> (fri (?leq (int 3) (int 2)))
(false)

> (fri (?leq (false) (true)))
(true)
```
- nasprotna vrednost (~ e1): Vrne nasprotno vrednost za izraze e1.
```
> (fri (~ (int 3)))
(int -3)

> (fri (~ (false)))
(true)
```
preverjanje tipov (?int e) se evalvira v (true), če je rezultat izraza e celo število tipa int.
```
> (fri (?int (int 5)))
(true)
```
vejitev (if-then-else condition e1 e2). Če se izraz condition evalvira v logično vrednost (true), je rezultat izraza e1 sicer pa e2. Semantika jezika določa, da se evalvira samo eden izmed izrazov e1 in e2.
```
> (fri (if-then-else (true) (int 5) (add (int 2) (int "a"))))
(int 5)
```

2.9.2 Makro

Implementirajte naslednje FR makre (ne uporabljaj Racket makrov, in ne popravljaj interpreterja!!).

conditional, ki bo omogočal pogojni stavek s poljubnim številom pogojev (podobno kot to počne cond v Racketu).

> (conditional (true) (int -100) (mul (true) (false)) (add (int 1) (int 1)) (int 9000))
(if-then-else
(true)
(int -100)
(if-then-else (mul (true) (false)) (add (int 1) (int 1)) (int 9000)))

(?geq e1 e2), ki preveri, ali je vrednost izraza e1 “večja” od e2. Definiran je za vse vrednosti, na katerih deluje ?leq.
```
> (?geq (add (int 1) (int 1)) (int 4))
(?leq (int 4) (add (int 1) (int 1)))
```

Rešitve nalog shranite v eno datoteko z imenom 08.rkt in jo oddajte na učilnici.

3 Seminarske naloge

3.1 1. seminarska naloga

FRI in izgubljeni urniki

Seminarska naloga 1 pri predmetu Funkcijsko programiranje
(Različica 1.1a)

3.1.1 Uvod — pogrešani urniki

Študentje fakultete FRI ne vejo, kateri cikel vaj izbrati, saj osebni urniki “ne delajo”. Panično si dopisujejo z asistenti.

V vsesplošni zmedi so asistenti FRI problem priprave urnikov predali študentom programa BMAG-RI. Le ti so se hitro posvetovali s kolegi programa BMAG-RM. Od njih so izvedeli, da problem priprave osebnih urnikov spada v razred NP problemov. Zvito so jim predlagali, da naj ta problem rešijo s prevedbo na problem SAT. Rešitev le tega naj poiščejo z Davis–Putnam–Logemann–Lovelandovim (DPLL) algoritmom. Za programski jezik naj izberejo Standardni ML.

3.1.2 Prvi del — logične formule in algoritem DPLL

Poljubne logične formule (izraze oz. izjave) lahko opišemo z naslednjim podatkovnim tipom 'a expression:

datatype 'a expression = 
    Not of 'a expression
|   Or of 'a expression list
|   And of 'a expression list
|   Eq of 'a expression list
|   Imp of 'a expression * 'a expression
|   Var of 'a
|   True | False;

Konstruktor Not predstavlja negacijo, Or predstavlja disjunkcijo, And konjunkcijo, Imp logično implikacijo ter Eq logično ekvivalenco. Podatkovni tip 'a expression je polimorfen, ker je tip imen logičnih spremenljivk (Var) poljuben. Za izpis “dolgih in globokih” izrazov lahko v SML uporabiš naslednje nastavitve:

Control.Print.printDepth := 100;
Control.Print.printLength := 1000;
Control.Print.stringDepth := 1000;

Da se izogneš opozorilu Warning: calling polyEqual, lahko na vrhu datoteke dodaš:

val _ = Control.polyEqWarn := false;

Preden se lotiš reševanja spodnjih problemov implemntiraj funkcijo isolate (= ''a list -> ''a list''), ki iz danega seznama odstrani duplikate tako, da ohrani le prvo pojavitev elementov z leve.

Primer.

- isolate [1,2,34,6,7,4,5,5,3,4,5,6,2,1,3,0];
val it = [1,2,34,6,7,4,5,3,0] : int list

V programskem jeziku SML implementiraj naslednje funkcije. V pomoč naj ti bodo funkcije:

infixr 1 $;
fun f $ x = f x;

fun eq a b = a = b;

fun neq a b = a <> b;

fun remove x = List.filter (neq x);

(✔️ 9 točk, 📜 11) getVars (= ''a expression -> ''a list)

Sprejme logično formulo in vrne imena spremenljivk (brez ponavljanja) v obliki seznama. Vrstni red spremenljivk naj bo od leve proti desni. Tukaj je smiselna uporaba mutacij.

Primer.
```
- getVars (Eq [Var "A", Var "B", Imp (Var "D", Not (Var "Q")), Var "D", Var "B"]);
val it = ["A","B","D","Q"] : string list
```
Priporočene funkcije: List.map, List.concat, List.@, isolate, ali pa List.app, before, !, :=, List.all.
(✔️ 9 točk, 📜 8) eval (= fn: ''a list -> ''a expression -> bool)

Sprejme seznam spremenljivk in logično formulo. Uporablja naj currying. Vrne izračunano vrednost podanega izraza, v kateri uporabi logično vrednost true za spremenljivke, ki se nahajajo v vhodnem seznamu, za vse ostale pa false.

Konjunkcijo (And), disjunkcijo (Or) in ekvivalenca (Eq) posplošimo iz dveh argumentov na poljubno mnogo — za argument prejmejo seznam, na naslednji način:

\[ \begin{align*} \text{And } E &:= \bigwedge_{e \in E} e \sim (e_1 \wedge e_2 \wedge e_3 \wedge ...) \\ \text{Or } E &:= \bigvee_{e \in E} e \sim (e_1 \vee e_2 \vee e_3 \vee ...) \\ \text{Eq } E &:= \bigwedge_{e_1,e_2 \in E} (e_1 \Leftrightarrow e_2) \sim ((e_1 \Leftrightarrow e_2) \wedge (e_2 \Leftrightarrow e_3) \wedge (e_3 \Leftrightarrow e_4) \wedge \ldots) \end{align*} \]

\[ \begin{align*} \text{And } E &:= \bigwedge_{e \in E} e \sim (e_1 \wedge e_2 \wedge e_3 \wedge \ldots) \\ \text{Or } E &:= \bigvee_{e \in E} e \sim (e_1 \vee e_2 \vee e_3 \vee \ldots) \\ \text{Eq } E &:= \bigwedge_{e_1,e_2 \in E} (e_1 \Leftrightarrow e_2) \sim ((e_1 \Leftrightarrow e_2) \wedge (e_2 \Leftrightarrow e_3) \wedge (e_3 \Leftrightarrow e_4) \wedge \ldots) \end{align*} \]

V primeru praznega seznama je pri funkciji Or rezultat False, v primeru funkcij And in Eq pa True. Pomisli, kaj je rezultat za te tri funkcije, ko ima seznam le en element (v pomoč naj ti bo primer, ko imaš prazen seznam).

\[ \begin{align*} \text{And } [] &:= \bigwedge_{e \in \{\}} e \sim 1 \\ \text{And } [e] &:= \bigwedge_{e \in \{e\}} e \sim e \\ \text{Or } [] &:= \bigwedge_{e \in \{\}} e \sim 0 \\ \text{Or } [e] &:= \bigwedge_{e \in \{e\}} e \sim e \\ \text{Eq } [] &:= \bigwedge_{e_1,e_2 \in \{\}} (e_1 \Leftrightarrow e_2) \sim 1 \\ \text{Eq } [e] &:= \bigwedge_{e_1,e_2 \in \{e\}} (e_1 \Leftrightarrow e_2) \sim e \Leftrightarrow e \sim 1 \end{align*} \]

(Logicna funckcija Eq es je True natako tedaj, ko se vsi elemeti v seznamu es evalvirjo v isto logično vrednost)

Primera.
```
- eval [2, 3]
   (And [True, Or [Var 1, Not (Not (Var 2))], Imp (Var 1, Var 2)]);
val it = true : bool

- eval [] (Eq [Var 1, False, False, True]);
val it = false : bool
```
Priporočene funkcije: List.exist, List.all, o.
(✔️ 9 točk, 📜 9) rmEmpty (= fn: 'a expression -> 'a expression)

Poenostavi logično formulo tako, da s konstantami (True in False) smiselno zamenja izraze logičnih funkcij Or, And in Eq, katerih argument je prazen seznam. Odstrani logične funkcije Or, And in Eq, če je argument le-teh seznam z enim samim elementom (Eq je poseben).

Primer.
```
- rmEmpty (Or [And [Or [Eq [Not (Var 0)]]], True]);
val it = Or [True,True] : int expr
```
Priporočene funkcije: List.map.

(✔️ 10 točk, 📜 16, 🔥 rmEmpty) pushNegations (= fn: 'a expression -> 'a expression)

Poenostavi logično formulo tako, da “potisne” vse negacije Not do listov drevesa logične formule, tj. do spremenljivk oz. konstant. Odpravi naj dvojne (ali večkratne) negacije. V pomoč naj ti bodo De Morganovi zakoni. V primeru negacije ekvivalence “potisni” negacijo po levi strani oz. veji.

Pravila:

$\neg(\neg A) \sim A$

$\neg(A \land B) \sim \neg A \lor \neg B$

$\neg(A \land B \land C) \sim \neg A \lor \neg B \lor \neg C$

$\neg(A \lor B) \sim \neg A \land \neg B$

$\neg(A \lor B \lor C) \sim \neg A \land \neg B \land \neg C$

$\neg(A \Rightarrow B) \sim A \land \neg B$

$\neg(A \Leftrightarrow B) \sim (\neg A \lor \neg B) \land (A \lor B)$

$\neg(A \Leftrightarrow B \Leftrightarrow C) \sim (\neg A \lor \neg B \lor \neg C) \land (A \lor B \lor C)$

Primera.

- pushNegations (Not (Imp (Not (Not (Var "a")), True)));
val it = And [Var "a",Not True] : string expr

- pushNegations (Not (Eq [False, Var 3, Not (And [And [], Or [Var 1, Not (Eq [])], Imp (True, Var 2)])]));
val it = And [Or [Not False,Not (Var 3),And [True,Or [Var 1,Not True],Imp (True,Var 2)]],Or [False,Var 3,Or [Not True,And [Not (Var 1),True],And [True,Not (Var 2)]]]] : int expr

Zaradi lažje implementacije naj funkcija naprej pokliče nad izrazom funkcijo rmEmpty. Priporočene funkcije: List.map, o.

(✔️ 10 točk, 📜 33, 🔥 rmEmpty) rmConstants (= fn: ''a expression -> ''a expression)

Poenostavi logično formulo tako, da odstrani vse konstante (True in False) na smiseln način, tj. upošteva lastnosti izjavnega računa. Na koncu je izraz samo konstanta ali pa izraz brez konstant. Zaradi lažje implementacije naj funkcija naprej pokliče nad izrazom funkcijo rmEmpty. Rezultata funkcije rmConstants naj se ne da več poenostaviti z rmEmpty.

Pravila:

$A \land 0 \sim 0$	$A \lor 0 \sim A$	$A = 0 \sim \neg A$	$A \Rightarrow 0 \sim \neg A$
$A \land 1 \sim A$	$A \lor 1 \sim 1$	$A = 1 \sim 1$	$A \Rightarrow 1 \sim A$
$A \land 1 \land 1 \sim A$	$A \lor 0 \lor 0 \sim A$	$0 = A \sim 1$	$\neg 0 \sim 1$
$A \land 1 \land 0 \sim 0$	$A \lor 0 \lor 1 \sim 1$	$1 = A \sim A$	$\neg 1 \sim 0$

$Eq[A,0,1] \sim 0$

$Eq[A,1,1] \sim A$

$Eq[A,0,0] \sim \neg A$

$Eq[A,B,1,C] \sim A \land B \land C$

$Eq[A,B,0,C] \sim \neg A \land \neg B \land \neg C$

Primeri.

- rmConstants (Eq [True, Var 1, Var 2]);
val it = And [Var 1,Var 2] : int expression

- rmConstants (Eq [Var 1, False, Var 2]);
val it = And [Not (Var 1),Not (Var 2)] : int expression

- rmConstants (Eq [Var 1, Eq [False, Var 3, And [And [], Or [Var 1, Not (Eq [Var 4, False, True])], Imp (True, Var 2)]]]);
val it = Eq [Var 1,And [Not (Var 3),Not (Var 2)]] : int expression

Priporočene funkcije: List.map, List.exists, remove, eq, neg.

fun neg True = False
|   neg False = True
|   neg e = Not e;

(✔️ 9 točk, 📜 14, 🔥 rmEmpty) rmVars (= fn: ''a expression -> ''a expression)

Poenostavi logično formulo tako, da združi oz. odstrani ponavljajoče se spremenljivke na smiseln način, tj. izkorišča lastnost idempotentnosti v primeru konjunkcije, disjunkcije, ekvivalence in implikacije.

Pravila:

$A \land A \sim A$

$A \land B \land A \sim A \land B$

$A \lor A \sim A$

$A \lor B \lor A \sim A \lor B$

$A \Rightarrow A \sim 1$

$A \Leftrightarrow A \sim 1$

$A \Leftrightarrow A \Leftrightarrow B \sim A \Leftrightarrow B$

$A \Leftrightarrow B \Leftrightarrow A \sim A \Leftrightarrow B$

Primeri.

- rmVars (Or [Var "a", Var "a", Not (Var "b"), Not (Var "b")]);
val it = Or [Var "a",Not (Var "b")] : string expression

- rmVars (Imp (And [Var 0, Var 0] , Or [Var 0, Var 0]));
val it = True : int expression

- rmVars (Imp (And [Var 0, Var 1] , And [Var 1, Var 0]));
val it = Imp (And [Var 0,Var 1],And [Var 1,Var 0]) : int expression

- rmVars (And [Var "A", Var "B", Var "A"] );
val it = And [Var "A",Var "B"] : string expression

Zaradi lažje implementacije naj funkcija naprej pokliče nad izrazom funkcijo rmEmpty. Priporočene funkcije: List.map, isolate.

(✔️ 6 točk, 📜 6, 🔥 rmVars pushNegations rmConstants) simplify (= fn: ''a expression -> ''a expression)

Poenostavi oz. zmanjša število logičnih operatorjev, spremenljivk in konstant v logični formuli z uporabo do sedaj definiranih funkcij. Formulo poenostavlja toliko krat, da se je ne da več poenostavit z do sedaj definiranimi funkcijami. Zaradi lažjega testiranja je vrstni red apliciranja funkcij fiksen, tj. 1. rmConstants, 2. pushNegations in na koncu 3. rmVars.

Primer.
```
- simplify (Eq [True, Eq [False,Var 3, And [And [], Or [Var 1, Not (Eq [Var 4, False, True])], Imp (True, Var 2)]], True, Eq [Not (Var 3), Var 2]]);
val it = And [And [Not (Var 3), Not (Var 2)], Eq [Not (Var 3), Var 2]] : int expr
```

(bonus naloga, ✔️ 8 točk, 📜 10, 🔥 getVars eval) prTestEq (= fn: int -> ''a expression -> ''a expression -> bool)

Z uporabo funkcij lcg in int2bool naključno izbere vrednosti spremenljivk, ki se nahajajo v vhodnih izrazih.

datatype 'a stream = Next of 'a * (unit -> 'a stream);

fun lcg seed =
   let fun lcg seed =
      Next (seed, fn () =>
            lcg (LargeInt.mod (1103515245 * seed + 12345, 0x7FFFFFFF)))
   in lcg (LargeInt.fromInt seed)
   end;

fun int2bool i = LargeInt.mod (i, 2) = 1;

Prvi argument je seme za lcg. Najprej izbere vrednosti za prvi izraz in potem za drugi (samo za spremenljivke, ki se ne pojavijo v prvem seznamu). Vrstni red spremenljivk (pri izbiranju vrednosti) je od leve proti desni (glej fun. getVars). Na koncu evalvira izraza za generirano izbiro spremenljivk in vrne true, če sta rezultata enaka.

Testiranje.

- val exp1 = (Eq [True, Eq [False, Var 3, And [And [], Or [Var 1, Not (Eq [Var 4, False, True])], Imp (True, Var 2)]]]);
- val exp2 = And [Not (Var 3), Not (Var 2)];
- val exp3 = And [Not (Var 1), Not (Var 2)];

- List.tabulate (20, (fn i => (i, prTestEq i exp1 exp2)));
val it =
[(0,true),(1,true),(2,true),(3,true),(4,true),(5,true),(6,true),(7,true),
(8,true),(9,true),(10,true),(11,true),(12,true),(13,true),(14,true),
(15,true),(16,true),(17,true),(18,true),(19,true)] : (int * bool) list

- List.tabulate (20, (fn i => (i, prTestEq i exp1 exp3)));
val it =
[(0,false),(1,true),(2,true),(3,true),(4,false),(5,false),(6,true),(7,true),
(8,true),(9,true),(10,true),(11,true),(12,false),(13,false),(14,true),
(15,true),(16,true),(17,true),(18,true),(19,true)] : (int * bool) list

(✔️ 16 točk, 📜 30-40, 🔥 getVars) satSolver (= fn: ''a expression -> ''a list option)

Za vhodno logično formulo (v obliki KNO — funkcija isCNF vrne true) poskuša poiskati take vrednosti spremenljivk, da se bo formula evalvirala v vrednost True. Ker taka izbira vrednosti spremenljivk ne obstaja vedno, funkcija vrača rezultat, kot opcijo. Funkcija satSolver vrne le spremenljivke (imena), ki jih je potrebno nastaviti na True, za ostale pa predpostavimo, da so False. Če vhodni izraz ni v obliki KNO, funkcija proži izjemo exception InvalidCNF.

fun isCNF (And es) =
List.all
   (fn Or es => List.all (fn (Var _ | Not (Var _)) => true | _ => false) es
   |   (Var _ | Not (Var _)) => true
   |   _ => false) es
|   isCNF (Or es) = List.all (fn (Var _ | Not (Var _)) => true | _ => false) es
|   isCNF (True | False | Var _ | Not (Var _)) = true
|   isCNF _ = false;

exception InvalidCNF;

Pri implementaciji si pomagaj z algoritmom DPLL. Namen algoritma DPLL je izbrati vrednosti spremenljivk tako, da se bodo vsi “Or izrazi” (in ostale izolirane spremenljivke) v vhodni logični formuli evalvirali v True.

Algoritem skuša poiskati tako rešitev s preiskovanjem v globino. Pri tem izbira vrednosti spremenljivke tako, da zadosti vsaj enemu izmed “Or izrazov” v trenutnem izrazu. Ko se odloči za spremenljivko in njeno vrednost, trenuten izraz poenostavi. Če se izraz poenostavi v False, algoritem se vrne nazaj (backtracking) in poskuša z negirano vrednostjo izbrane spremenljivke. Če tudi to ne uspe, vrne ni rešitve. Če se izraz ne poenostavi niti v False niti v True, potem algoritem rekurzivno nadaljuje z preiskovanjem v globino.

Algoritem DPLL naj vodi evidenco o “odstranjenih” spremenljivkah in njihovih vrednostih (kar služi kot izhod funkcije satSolver). Odstranjene spremenljivke so tiste, katerim smo že določili vrednost, v samem izrazu pa ne nastopajo več. Koraki algoritma so naslednji:

korak: Poišči spremenljivko, ki stoji sama (je oblike Or [<var>], Or [Not <var>], Not <var>, oz. Var <name>).

V primeru Or [<var>] oz. Var <name> v seznam “odstranjenih” spremenljivk dodamo ime <name>, v primeru Or [Not (Var <name>)] oz. Not (Var <name>) pa nič.

Trenutno logično formulo poenostavimo tako, da vse ponovitve izbrane spremenljivke zamenjamo s konstanto (tako, da je vrednost izraza Or [<var>], Or [Not <var>], Not <var>, oz. Var <name> enaka True. Ta korak ponavljamo, dokler nimamo več izoliranih spremenljivk. Po koraku 1. V formuli ne nastopa nobena konstanta (če formula le ni enaka True oz. False).
korak: Če je trenutna logična formula enaka And [] oz. True, potem smo z izvajanjem algoritma končali (smo našli take vrednosti spremenljivk, da se je formula evalvirala v vrednost True) in vrnemo seznam imen spremenljivk, ki smo jih nastavili na True.

Če logična formula vsebuje izraz Or [] oz. je vrednost trenutne logične formule enaka False, vrnemo NONE. V nasprotnem primeru nadaljujemo s korakom 3.
korak: Izberemo eno poljubno spremenljivko v logični formuli ter jo nastavimo na tako vrednost, da se bo logična funkcija Or, ki vsebuje izbrano spremenljivko, evalvirala v logično vrednost True. Z izbiro vrednosti izbrane spremenljivke formulo poenostavimo (na podoben način kot v 1. koraku). Nad dobljeno formulo rekurzivno izvedemo algoritem DPLL.

Če je rezultat rekurzivnega klica NONE, potem izvedemo še en rekurziven klic, ampak v tem primeru izberemo negirano vrednost izbrane spremenljivke (logično formulo tudi ustrezno poenostavimo). Če je tudi v tem primeru rekurziven klic neuspešen, vrnemo NONE.

Namig. Za poenostavljanje ne uporabljaj funkcije simplify.

Primeri.

- val t1 = satSolver (True : int expr);
val t1 = SOME [] : int list option

- val t2 = satSolver (False : int expr);
val t2 = NONE : int list option

- val t3 = satSolver (And [] : int expr);
val t3 = SOME [] : int list option

- val t4 = satSolver (And [Or []] : int expression);
val t4 = NONE : int list option

- val t5 = satSolver (And [Or [Var 1]]);
val t5 = SOME [1] : int list option

- val t6 = satSolver (And [Or [Var 1, Not (Var 2)]]);
val t6 = SOME [1] : int list option (* ali pa SOME [] *)

- val t7 = satSolver (And [Or [Var 1, Not (Var 1)]]);
val t7 = SOME [] : int list option (* ali pa SOME [1] *)

- val t8 = satSolver (And [Or [Var 1, Var 3], Or [Not (Var 1), Not (Var 3)], Or[Not (Var 3), Var 1]]);
val t8 = SOME [1] : int list option

- val t9 = satSolver (And [Or [Var 1, Var 3], Or [Not (Var 1), Not (Var 3)], Or[Not (Var 3), Var 1], Or[Var 3, Not (Var 1)]]);
val t9 = NONE : int list option

- val t10 = satSolver (And [Or [Not (Var 1), Not (Var 5), Var 7, Var 7], Or [Var 1, Var 4, Not (Var 7)], Or [Not (Var 1), Var 6, Not (Var 7), Var 7, Var 7], Or [Var 2, Var 5, Not (Var 7), Var 7], Or [Not (Var 4), Var 7, Var 7, Var 7], Or [Var 7, Var 7, Var 7, Not (Var 7)], Or [Var 2, Not (Var 7), Var 7], Or [Not (Var 3), Not (Var 1), Var 7, Var 7], Or [Var 5, Var 4, Not (Var 7)], Or [Var 3, Var 6, Not (Var 7), Var 7], Or [Var 3, Var 1, Var 5, Not (Var 7)], Or [Var 2, Var 5, Not (Var 7)], Or [Not (Var 1), Not (Var 4), Var 7], Or [Not (Var 2), Not (Var 4), Var 7, Var 7], Or [Not (Var 2), Not (Var 5), Not (Var 7), Var 7], Or [Not (Var 3), Not (Var 6), Not (Var 7), Not (Var 7)], Or [Var 3, Var 2, Not (Var 7)], Or [Var 5, Var 6], Or [Not (Var 2), Not (Var 5), Var 7, Var 7, Var 7], Or [Var 3, Var 6], Or [Var 1, Var 5, Var 4, Not (Var 7)], Or [Not (Var 3), Not (Var 5), Var 7, Not (Var 7), Not (Var 7)], Or [Not (Var 3), Var 1, Not (Var 5), Not (Var 7), Not (Var 7)], Or [Var 2, Var 6], Or [Var 1, Not (Var 7)], Or [Not (Var 6), Not (Var 5), Not (Var 7), Not (Var 7)], Or [Var 5, Not (Var 7), Var 7], Or [Not (Var 2), Var 5, Var 7, Not (Var 7)], Or [Not (Var 6), Not (Var 4), Var 7, Not (Var 7)], Or [Var 3, Var 2, Var 1, Not (Var 7)], Or [Not (Var 3), Var 1, Not (Var 6), Var 4, Not (Var 7), Not (Var 7)], Or [Var 6, Not (Var 7)], Or [Var 3, Not (Var 7)], Or [Var 2, Var 3], Or [Not (Var 2), Not (Var 1), Not (Var 6), Not (Var 5), Not (Var 7), Not (Var 7)], Or [Not (Var 2), Var 5, Var 7], Or [Var 3, Var 5], Or [Not (Var 3), Not (Var 2), Not (Var 7), Not (Var 7)], Or [Not (Var 2), Not (Var 5), Var 7, Not (Var 7), Var 7, Not (Var 7)], Or [Var 2, Not (Var 5), Var 7], Or [Var 2, Var 6, Var 4, Not (Var 7)], Or [Var 2, Not (Var 5), Var 7, Not (Var 7)], Or [Var 6, Var 5, Not (Var 7)], Or [Var 4, Not (Var 7)], Or [Var 3, Var 6, Not (Var 7), Not (Var 7)]])
val t10 = SOME [3,6] : int list option (* ali pa SOME [6,3] *)

Priporočene funkcije: List.map, isolate, neg.

fun neg True = False
|   neg False = True
|   neg (Not e) = e
|   neg e = Not e;

setVar : 'a expression -> 'a expression -> 'a expression
singleton : 'a expression -> 'a expression option
rmSingeltons : 'a expression -> 'a list -> 'a expression * 'a list
dpll : 'a expression -> 'a list -> 'a list option

3.1.3 Drugi del — reševanje problema urnikov

Asistenti so študentom posredovali naslednja podatka:

Termine vaj za posamezen predmet. Primer (dva predmeta, skupno osem ciklov vaj):

val timetable =
   [{day = "cetrtek", time = 8, course = "RK"},
   {day = "torek", time = 7, course = "DS"},
   {day = "sreda", time = 10, course = "DS"},
   {day = "petek", time = 14, course = "DS"},
   {day = "sreda", time = 10, course = "ARS"},
   {day = "petek", time = 14, course = "ARS"},
   {day = "torek", time = 7, course = "P2"},
   {day = "ponedeljek", time = 12, course = "P2"}] : timetable

Predmetnik za vsakega študenta. Primer (dva študenta z različnima predmetnikoma):

val students =
   [{studentID = 63170000, curriculum = ["DS", "P2"]},
   {studentID = 63160000, curriculum = ["P2", "RK", "ARS"]}] : student list

Sinonima timetable in student predstavljata naslednja tipa:

type timetable = {day : string, time: int, course: string} list
type student = {studentID : int, curriculum : string list}

Implementiraj naslednje funkcije:

(✔️ 16 točk, 📜 32) problemReduction (= fn: int -> timetable -> student list -> <customEqType> expression)

Problem urnikov predstavi z logično formulo v obliki KNO. Prvi argument je število prostih mest na vsakih vajah. Vaje se izvajajo le eno uro. Ker je podatkovni tip logičnih izrazov polimorfen ('a expression), lahko podatkovni tip imen spremenljivk izbereš poljubno (npr. ime lahko predstavimo kot četverko (s : int, c : string, t : string * int , p : int)).

Izbiro cikla vaj pri posameznem predmetu lahko predstavimo z logičnimi spremenljivkami $x_{s,c,t,p}$. Spremenljivka $x_{s,c,t,p}$ ima štiri indekse. Indeks $s$ določa študenta, indeks $c$ določa predmet, indeks $t$ določa cikel vaj in indeks $p$ mesto oz. označen sedež na vajah. Če ima spremenljivka $x_{s,c,t,p}$ logično vrednost true, to pomeni, da študent $s$, pri predmetu $c$, obiskuje cikel vaj $t$ in sedi na sedežu $p$ (in obratno, če ima logično vrednost false).

Želimo, da logična formula v obliki KNO opiše naslednje lastnosti:

Vsak študent obiskuje (vsaj) en cikel vaj za vsak premet njegovega predmetnika.

To nam da naslednji del formule v CNF.

\[ \bigwedge_{s\in S} \bigwedge_{c\in C_s} \bigvee_{t\in T_c} \bigvee_{p\in P_t} x_{s,c,t,p} \]

Znak $\vee$ predstavlja disjunkcijo, znak $\wedge$ pa konjunkcijo. Množica $S$ prestavlja študente, množica $C_s$ predstavlja predmete študenta $S$, množica $T_c$ predstavlja možne cikle vaj pri predmetu $C$ in množica $P_t$ sedišča pri ciklu vaj $t$.
Izbrani cikli vaj se nobenemu izmed študentov ne prekrivajo.

\[\bigwedge_{s\in S} \bigwedge_{\substack{c_1,c_2\in C_s \\ t_1\in T_{c_1}, t_2\in T_{c_2} \\ \text{time}(t_1)=\text{time}(t_2) \\ p_1\in P_{t_1}, p_2\in P_{t_2} \\ (c_1,p_1)\neq(c_2,p_2)}} (\neg x_{s,c_1,t_1,p_1} \vee \neg x_{s,c_2,t_2,p_2})\]

Oznake imajo enak pomen kot v prejšnji točki. Oznaka $\neg$ predstavlja negacijo. Funkcija time za dan cikel vaj vrne začetek izvajanja. Opisana logična formula v obliki KNO pravi, da noben študent ni na dveh ciklih vaj istočasno in da ne sedi pri istemu ciklu na dveh ali več sedežnih.

Opomba: ti pogoji ne ovirajo študenta pri obiskovanju več ciklov vaj za isti premet.

Optimizacija: namesto pogoja $(c_1, p_1) \neq (c_2, p_2)$ lahko uporabiš pogoj $(c_1, p_1) \prec (c_2, p_2)$, ki pravi, da je prvi par $(c_1, p_1)$ leksikografsko pred pred drugim parom $(c_2, p_2)$.
Na vsakem stolu sedi največ en študent.

\[\bigwedge_{c\in C} \bigwedge_{t\in T_c} \bigwedge_{p\in P_t} \bigwedge_{\substack{s_1,s_2\in S_c \\ s_1 \neq s_2}} (\neg x_{s_1,c,t,p} \vee \neg x_{s_2,c,t,p})\]

Množica $S_c$ predstavlja množico študentov, ki so vpisani v predmet $C$. Logična formula pa pravi, da noben par študentov ne sedi na istem stolu pri istih vajah istega predmeta.

Podobno kot v prejšnji točki lahko uporabiš pogoj $s_1 \prec p_1$ namesto pogoja $s_1 \neq p_1$.

Primer (ni edina pravilna rešitev).

- problemReduction 2 timetable students;
val it =
And [
   -- lastnost 1:
   Or
   [Var (63170000,"DS",("torek",7),1),Var (63170000,"DS",("torek",7),2),
      Var (63170000,"DS",("sreda",10),1),Var (63170000,"DS",("sreda",10),2),
      Var (63170000,"DS",("petek",14),1),Var (63170000,"DS",("petek",14),2)],
   Or
   [Var (63170000,"P2",("torek",7),1),Var (63170000,"P2",("torek",7),2),
      Var (63170000,"P2",("ponedeljek",12),1),
      Var (63170000,"P2",("ponedeljek",12),2)],
   Or
   [Var (63160000,"P2",("torek",7),1),Var (63160000,"P2",("torek",7),2),
      Var (63160000,"P2",("ponedeljek",12),1),
      Var (63160000,"P2",("ponedeljek",12),2)],
   Or
   [Var (63160000,"RK",("cetrtek",8),1),
      Var (63160000,"RK",("cetrtek",8),2)],
   Or
   [Var (63160000,"ARS",("sreda",10),1),
      Var (63160000,"ARS",("sreda",10),2),
      Var (63160000,"ARS",("petek",14),1),
      Var (63160000,"ARS",("petek",14),2)],
   Or

   -- lastnost 2:
   [Not (Var (63170000,"DS",("torek",7),1)),
      Not (Var (63170000,"DS",("torek",7),2))],
   Or
   [Not (Var (63170000,"DS",("sreda",10),1)),
      Not (Var (63170000,"DS",("sreda",10),2))],
   Or
   [Not (Var (63170000,"DS",("petek",14),1)),
      Not (Var (63170000,"DS",("petek",14),2))],
   Or
   [Not (Var (63170000,"DS",("torek",7),1)),
      Not (Var (63170000,"P2",("torek",7),1))],
   Or
   [Not (Var (63170000,"DS",("torek",7),1)),
      Not (Var (63170000,"P2",("torek",7),2))],
   Or
   [Not (Var (63170000,"DS",("torek",7),2)),
      Not (Var (63170000,"P2",("torek",7),1))],
   Or
   [Not (Var (63170000,"DS",("torek",7),2)),
      Not (Var (63170000,"P2",("torek",7),2))],
   Or
   [Not (Var (63170000,"P2",("torek",7),1)),
      Not (Var (63170000,"P2",("torek",7),2))],
   Or
   [Not (Var (63170000,"P2",("ponedeljek",12),1)),
      Not (Var (63170000,"P2",("ponedeljek",12),2))],
   Or
   [Not (Var (63160000,"P2",("torek",7),1)),
      Not (Var (63160000,"P2",("torek",7),2))],
   Or
   [Not (Var (63160000,"P2",("ponedeljek",12),1)),
      Not (Var (63160000,"P2",("ponedeljek",12),2))],
   Or
   [Not (Var (63160000,"RK",("cetrtek",8),1)),
      Not (Var (63160000,"RK",("cetrtek",8),2))],
   Or
   [Not (Var (63160000,"ARS",("sreda",10),1)),
      Not (Var (63160000,"ARS",("sreda",10),2))],
   Or
   [Not (Var (63160000,"ARS",("petek",14),1)),
      Not (Var (63160000,"ARS",("petek",14),2))],
   Or

   -- lastnost 3:
   [Not (Var (63160000,"P2",("torek",7),1)),
      Not (Var (63170000,"P2",("torek",7),1))],
   Or
   [Not (Var (63160000,"P2",("torek",7),2)),
      Not (Var (63170000,"P2",("torek",7),2))],
   Or
   [Not (Var (63160000,"P2",("ponedeljek",12),1)),
      Not (Var (63170000,"P2",("ponedeljek",12),1))],
   Or
   [Not (Var (63160000,"P2",("ponedeljek",12),2)),
      Not (Var (63170000,"P2",("ponedeljek",12),2))]]
: (int * string * (string * int) * int) expression

Priporočene funkcije: isolate, $, List.map, List.filter, exists, eq, o, List.tabulate, List.concat, List.@.

(✔️ 6 točk, 📜 12) solutionRepresentation (= fn: <customEqType> list option -> (student * timetable) list option)

Rezultat funkcije SATsolver smiselno predstavi kot seznam parov (študent, urnik).

Primera (možnih rešitev je veliko).

- solutionRepresentation (satSolver (problemReduction 2 timetable students));
val it =
SOME
   [({curriculum=["ARS","RK","P2"],studentID=63160000},
   [{course="ARS",day="petek",time=14},{course="ARS",day="sreda",time=10},
      {course="RK",day="cetrtek",time=8},
      {course="P2",day="ponedeljek",time=12},
      {course="P2",day="torek",time=7}]),
   ({curriculum=["P2","DS"],studentID=63170000},
   [{course="P2",day="ponedeljek",time=12},
      {course="DS",day="petek",time=14},{course="DS",day="sreda",time=10},
      {course="DS",day="torek",time=7}])] : (student * timetable) list option

- solutionRepresentation (satSolver (problemReduction 1 timetable students));
val it =
SOME
   [({curriculum=["ARS","P2","RK"],studentID=63160000},
   [{course="ARS",day="petek",time=14},{course="ARS",day="sreda",time=10},
      {course="P2",day="torek",time=7},{course="RK",day="cetrtek",time=8}]),
   ({curriculum=["DS","P2"],studentID=63170000},
   [{course="DS",day="petek",time=14},{course="DS",day="sreda",time=10},
      {course="P2",day="ponedeljek",time=12},
      {course="DS",day="torek",time=7}])] : (student * timetable) list option

Priporočene funkcije: $, eq, List.filter, o, ListPair.unzip, List.map, isolate.

3.1.4 Oddaja seminarske naloge

Oddati je potrebno eno datoteko 01-project.sml. Oddana SML datoteka naj vsebuje vse funkcije (označene z ✔️). Neimplementirane funkcije naj ob klicu prožijo izjemo NotImplemented.

Drugi del mora biti oddan v celoti, zaradi avtomatskega testiranja. Skupno število točk ne more preseči 100.

Oddana seminarska naloga bo ocenjena glede na naslednji točkovnik:

funkcija	točke
`getVars`	9
`eval`	9
`rmEmpty`	9
`pushNegations`	10
`rmConstants`	10
`rmVars`	9
`simplify`	6
`prTestEq`	8
`satSolver`	16
`problemReduction`	16
`solutionRepesesntation`	6
skupaj	100 (+8 bonus)

Seminarska naloga je uspešno opravljena, če si prejel vsaj 45 točk iz funkcij označenih z ✔️ in si opravil ustni zagovor.

3.1.5 Še nekaj napotkov

Začni z datoteko 01-project-empty.sml.
Če je predpisan tip funkcije 'a expression -> 'a expression, potem tip ''a expression -> ''a expression ni dovolj.
Nedokončno (< 50%) implementirane funkcije, naj prožijo izjemo, kot piše v navodilih.
Pri pri implementaciji funkcije rmVars se držimo istega načina odstranjevanja dupliciranih spremenljivk, kot pri funkciji getVars, tj:
```
- rmVars (And [Var "A", Var "B", Var "A"] );
val it = And [Var "A",Var "B"] : string expression
```
Če nisi uspešno implementiral funkcije satSolver, lahko še vedno rešujes 2. del. V tem primeru lahko uporabiš funkcijo external_sat_solver: ''a expression -> ''a list option, ki se nahaja v datoteki external_sat_solver.sml. SML skripta uporablja program CryptoMiniSat, ki si ga je potrebno dodatno namestiti. Če uporabljaš Windows si prenesi datoteko cryptominisat5-win-amd64-nogauss.exe in jo shrani v mapo, kjer imaš projekt, če pa uprabljas Linux si pa prenesi datoteko cryptominisat5_amd64_linux_static.gz in jo razpakiraj v datoteko cryptominisat5_amd64_linux. Poskrbi, da bo ta program izvedljiv (v lupini poženi chmod u+x cryptominisat5_amd64_linux). IZVORNO KODO DATOTEKE external_sat_solver.sml LAHKO UPORABLJAŠ SAMO ZA TESTIRANJE IMPLEMENTACIJE 2. DELA PROJEKTA. POSKRBI, DA TVOJA ODDAJA NE VSEBUJE TE IZVORNE KODE.

3.1.6 Javni testi

Glej testno datoteko 01-public-tests-project.sml.

3.2 2. Seminarska naloga

FRInterpreter

Seminarska naloga 2 pri predmetu Funkcijsko programiranje
ver. 1.0

V tem seminarju boste implementirali interpreter za programski jezik FR in vse konstrukte, ki so potrebni, da lahko v njem pišemo programe.

Klic interpreterja naj ima sintakso (fri expression environment), kjer expression predstavlja izraz v jeziku FR, environment pa spremenljivko, ki hrani začetno okolje.

Konstrukti jezika FR naj bodo definirani z Racket konstruktom struct. Uporabite jih za definicije konstruktov opisanih v sledečih odstavkih.

3.2.1 Podatkovni tipi

Logični vrednosti (true) in (false): (true) predstavlja resnično vrednost, (false) pa neresnično.
Cela števila (int n): n je celo število v Racket.
Zaporedja (.. e1 e2), : (empty) predstavlja konec zaporedja, (.. e1 e2) pa zaporedje, ki ga dobimo, če rezultat evalvacije izraza e1 dodamo na začetek zaporedja, ki ga dobimo kot rezultat evalvacije izraza e2.
Izjeme (exception exn): exn je niz (string) v Racket.

Če se katerikoli argument evalvira v sproženo izjemo je rezultat prva sprožena izjema. Ko interpreter naleti na prvo sprožena izjema, konča z interpretiranjem v širino/globino.

3.2.2 Nadzor toka

Dobro razumevanje programskih jezikov z izjemami je ključnega pomena, da pri reševanju te seminarske naloge ne izgubiš potrpljenja (╯°□°）╯︵ ┻━┻ !
V naprej si naredi načrt kako in kje vse boš pazil na izjeme. Kasnejše dodajanje “obližev” ponavadi vodi v zapravljanje časa.

Proženje izjem (trigger e): Če se izraz e evalvira v izjemo je rezultat sprožena izjema (triggered e), drugače pa je rezultat (triggered (exception "trigger: wrong argument type")).

Opomba: Sprožene izjeme niso veljaven del programa v jeziku FR, temveč so le interni mehanizem interpreterja.
Lovljenje izjem (handle e1 e2 e3):
- Če se izraz e1 evalvira v sproženo izjemo, je rezultat, kar ta sprožena izjema.
- Če se izraz e1 ne evalvira v izjemo je rezultat sprožena izjema "handle: wrong argument type" v FR.
- Če se izraz e2 evalvira v sprožena izjemo (ki ustreza izjemi e1) je rezultat evalviran izraz e3, drugače pa je rezultat evalviran izraz e2.
Vejitev (if-then-else condition e1 e2): Če se izraz condition evalvira v (false), potem je rezultat evalviran izraz e2, v vseh drugih primerih je rezultat evalviran izraz e1.
Preverjanje tipov (?int e), (?bool e), (?.. e), (?seq e), (?empty e), (?exception e): Funkcije vračajo (true), če je rezultat izraza e ustreznega tipa. V primeru (?seq e1) je rezultat (true) le, če se podano zaporedje konča z (empty).
Seštevanje (add e1 e2): Glede na tipe argumentov ločimo več primerov:
- Če sta izraza logični vrednosti je rezultat njuna disjunkcija (e1∨e2).
- Če sta izraza e1 in e2 celi števili, potem je rezultat njuna vsota.
- Če sta izraza e1 in e2 zaporedji (?seq), je rezultat seštevanja njuna združitev, tako da zaporedje e1 nadaljujemo z e2.
- Če izraza e1 in e2 nimata ustreznega tipa, je rezultat sprožena izjema "add: wrong argument type" v FR.
Množenje (mul e1 e2): Glede na tipe argumentov ločimo več primerov:
- Če sta izraza logični vrednosti je rezultat njuna konjunkcija (e1∧e2).
- Če sta izraza e1 in e2 celi števili, potem je rezultat njun produkt.
- Če izraza e1 in e2 nimata ustreznega tipa, je rezultat sprožena izjema "mul: wrong argument type" v FR.
Primerjanje (?leq e1 e2): Rezultat je logična vrednost v FR. Glede na tipe argumentov ločimo več primerov:
- Če sta izraza logični vrednosti je rezultat njuna implikacija e1 ⟹ e2.
- Če sta izraza e1 in e2 celi števili, potem je rezultat e1 ≤ e2.
- Če sta izraza zaporedji (?seq) je rezultat (true), če ima zaporedje e1 enako ali manjše število elementov kot zaporedje e2.
- Če izraza e1 in e2 nimata ustreznega tipa, je rezultat sprožena izjema "?leq: wrong argument type" v FR.
Ujemanje (?= e1 e2): Vrne rezultat (true), če se evalvirana izraza e1 in e2 ujemata oz. sta enaka.
Ekstrakcija (head e), (tail e):
- Za zaporedje e izraz (head e) vrne prvi element zaporedja, (tail e) pa preostali del zaporedja.
- Če izraz e nima ustreznega tipa, je rezultat sprožena izjema "head: wrong argument type" v FR (oz. "tail...").
- Če evalviran izraz e predstavlja konec zaporedja, je rezultat sprožena izjema "head: empty sequence" v FR (oz. "tail...").
Nasprotna vrednost (~ e): Vrne nasprotno vrednost za izraze e, ki se evalvirajo v bodisi logično vrednost ali celo število. Če izraz e nima ustreznega tipa, je rezultat sprožena izjema "~: wrong argument type" v FR.
Operatorja (?all e), (?any e):
- Če zaporedje (?seq) e ne vsebuje logične vrednosti (false), potem je rezultat izraza (?all e) enak (true), drugače pa (false).
- Če zaporedje (?seq) e vsebuje vsaj kašno vrednost, ki ni (false), potem je rezultat izraza (?any e) enak (true), drugače (false).
- Če izraz e ni zaporedje (?seq), je rezultat sprožena izjema "?all: wrong argument type" v FR (oz. "?any...").

Če se katerikoli argument evalvira v sproženo izjemo je rezultat prva (“od leve proti desni”) sprožena izjema (razen, če smo izjemo ulovili s handle).

3.2.3 Spremenljivke

Implementirajte spremenljivke in okolje za njihovo shranjevanje. Ko poženete interpreter naj bo okolje prazno. Med njegovim delovanjem so vrednosti shranjene in prebrane. Okolje naj bo predstavljeno s seznamom parov v jeziku Raket, ki naj bo naslednje oblike (list (var_name_1 . value_1) (var_name_2 . value_2) ... (var_name_n . value_n)). Definirate sledeča konstrukta za definicijo in uporabo spremenljivk.

Lokalno okolje (vars s e1 e2): Razširi trenutno okolje z imenom spremenljivke s, ki ima vrednost e1, ter v razširjenem okolju evalvira izraz e2. Če sta s in e1 Racket seznama, potem razširi trenutno okolje z vsemi imeni in vrednostmi v seznamih (analogno Racket-ovemu let izrazu) in evalvira izraz e2. (Če seznam s vsebuje podvojena imena, se proži FR izjema "vars: duplicate identifier" — se ne bo preverjalo).
Vrednost spremenljivke (valof s): Ob evalvaciji vrne vrednost spremenljivke. V okolju se lahko nahaja več spremenljivk z istim imenom, ki se med seboj senčijo. Izraz naj vrne pravilno vrednost spremenljivke, ki ni zasenčena. Če dana spremenljivka ni definirana je rezultat sprožena izjema "valof: undefined variable" v FR.

Če se katerikoli vrednost spremenljivk evalvira v sproženo izjemo je rezultat prva sprožena izjema.

3.2.4 Funkcije

Implementirajte funkcije, skripte (procedure) in klice. Funkcije uporabljajo leksikalni doseg, skripte pa dinamičnega. Definirajte sledeče konstrukte za delo s funkcijami, skriptami in klici:

Funkcije in procedure (fun name farg body), (proc name body): name predstavlja ime funkcije oz. procedure, podano v obliki Racket niza. fargs je Racket seznam argumentov in body predstavlja telo funkcije podano kot izraz v jeziku FR.

Če je ime funkcije prazen niz, gre za anonimno funkcijo. Vsi argumenti funkcije morajo imeti različna imena (Racket nize). (Če imajo argumenti podvojena imena, se proži FR izjema "fun: duplicate argument identifier" — se ne bo preverjalo).

Obravnavanje funkcij implementirajte tako, da ob interpretiranju programa se konstrukt fun evalvira v funkcijsko ovojnico (closure env f), kjer je f originalni konstrukt funkcije, env pa okolje na mestu, kjer je bila funkcija evalvirana.

Opomba: Funkcijske ovojnice niso veljaven del programa v jeziku FR, temveč so le interni mehanizem interpreterja. Funkcija je torej izraz, ki ga interpreter evalvira v ovojnico.

Funkcijski klici (call e args): Klic je definiran za vse izraze e, ki se evalvirajo bodisi v ovojnico ((closure ...) ali pa v proceduro ((proc ...). args je Racetov seznam izrazov, ki se evalvirajo v vrednosti argumentov. Pravila za evalvacijo so sledeča:
- Pri klicih funkcijskih ovojnic naj se okolje vsebovano v ovojnici razširi z imeni in vrednostmi argumentov (imena najdemo v opisu funkcije — fargs, vrednosti pa so priložene klicu — args) in imenom funkcije, ki ga povežemo z ovojnico (da omogočimo rekurzivne klice).
  
  Opomba: V primeru, da je ime funkcije enako imenu argumenta funkcije, argument zasenči funkcijo.
  
  V tako dobljenem okolju se izvede telo funkcije.
- Pri klicih procedur se telo funkcije izvede v lokalnem okolju (tistem, v katerem se izvede klic funkcij), ki mu dodamo le ime procedur. Ker procedure nimajo argumentov, kot seznam argumentov prejme prazen Racket seznam. Funkcijsko ovojnico optimizirajte tako, da iz nje izločite senčenja zunanjih spremenljivk, senčenja spremenljivk z lokalnimi argumenti in spremenljivke, ki v funkciji niso potrebne.
- Če se izraz e, ne evalvira v ovojnico ali pa v proceduro je rezultat sprožena izjema "call: wrong argument type" v FR.
- Če seznam args vsebuje premalo/preveč argumentov je rezultat sprožena izjema "call: arity mismatch".

Če se izraz e ali pa katerikoli od argumentov v args evalvira v sproženo izjemo je rezultat prva sprožena izjema.

Če pri ustvarjanju funkcijske ovojnice telo pripadajoče funkcije vsebuje nedefinirano zunanjo spremenljivko, interpreter vrne izjemo "closure: undefined variable".

3.2.5 Makro sistem

Napačno implementirani makri so vredni negativno število točk (uporaba define-syntax ali fri, popravljanje/poenostavljanje vhodnih izrazov, …). Na vajah se pogovori z asistentom glede pravilnosti tvoje rešitve.

Implementirajte funkcije v Racetu, ki bodo delovale kot makri v jeziku FR (glej predavanja!). Definirajte sledeče makre:

Večji (greater e1 e2): Preveri urejenost med elementoma. Definiran je za vse vrednosti, za katere je izraz (?leq e1 e2) legalen.
Obrni (rev e): Obrne vrstni red elementov zaporedja (?seq) e.
Pretvorba v dvojiški zapis (binary e1): Če je rezultat izraza e1 pozitivno celo število vrne zaporedje (?seq) bitov danega števila.
Mapping (mapping f seq): Vrne izraz (v jeziku FR), ki ima funkcionalnost funkcije List.map v Standard ML, a brez curryinga. f predstavlja izraz, ki se bo evalviral v funkcijsko ovojnico, seq pa izraz, ki se bo evalviral v zaporedje (?seq) elementov.
Filtering (filtering f seq): Vrne izraz (v jeziku FR), ki ima funkcionalnost funkcije List.filter v Standard ML, a brez curryinga. f predstavlja izraz, ki se bo evalviral v funkcijsko ovojnico, seq pa izraz, ki se bo evalviral v zaporedje (?seq) elementov.
Folding (folding f init seq): Vrne izraz (v jeziku FR), ki ima funkcionalnost funkcije List.foldl v Standard ML, a brez curryinga. f predstavlja izraz, ki se bo evalviral v funkcijsko ovojnico, init izraz, ki se bo evalviral v začetno vrednost, seq pa izraz, ki se bo evalviral v zaporedje (?seq) elementov.

Opomba: Makri naj podane izraze evalvirajo le enkrat.

3.2.6 Nadgradnja — mutacije in vzajemna rekurzija

Jeziku FR dodajte podporo za definicijo pravih spremenljivk in funkcij, ki so vzajemno rekurzivne. Način implementacije je prepuščen vam. To nadgradnjo boste zagovarjali ločeno.

3.2.7 Oddaja seminarske naloge

Nalogo oddajte v obliki ene datoteke z imenom 02-project.rkt.

Teste oddajte posebej. Koda naj bo dokumentirana.

Točkovanje bo izvedeno samodejno, svoje rešitve pa boste morali tudi zagovarjati. Samodejno testiranje bo izvedeno s testnimi primeri, ki ne bodo znani vnaprej. Oddana seminarska naloga bo ocenjena glede na naslednji točkovnik. Skupno število točk ne more preseči 100.

funkcionalnost	točke
Podatkovni tipi	9
Nadzor toka	17
Spremenljivke	9
Procedure, (rekurzivne) funkcije	24
Optimizacija ovojnic	11
Zahtevani makri	14
Mutacije in vzajemna rekurzija	10
slog kode	3
ustni zagovor	3
skupaj	= 100

Seminarska naloga je uspešno opravljena, čee si prejel vsaj 50 točk skupaj z zagovorom.

3.2.8 Primeri programov v jeziku FR

> (add (mul (true) (true)) (false))
(add (mul (true) (true)) (false))

> (fri (add (mul (true) (true)) (false)) null)
(true)

> (?seq (.. (int 1) (.. (int 2) (empty))))
(?seq (.. (int 1) (.. (int 2) (empty))))

> (fri (.. (?seq (.. (int 1) (.. (int 2) (empty))))
           (?seq (.. (int 1) (.. (int 2) (int 3))))) null)
(.. (true) (false))

> (fri (vars "a" (mul (int 12354) (int 2534)) (vars "b" (mul (int -3) (int 4))
             (mul (valof "a") (valof "b")))) null)
(int -375660432)

> (fri (vars (list "a" "b" "c" "d")
             (list (add (int 1) (int 2)) (mul (int -3) (int 4))
                   (~ (mul (int 1) (int 2))) (add (int -3) (int 4)))
             (.. (valof "c") (.. (.. (valof "d") (valof "c")) (empty)))) null)
(.. (int -2) (.. (.. (int 1) (int -2)) (empty)))

> (fri (call
      (fun "fib" (list "n")
           (if-then-else (?leq (valof "n") (int 2))
                         (int 1)
                         (add (call (valof "fib")
                                    (list (add (valof "n") (int -1))))
                              (call (valof "fib")
                                    (list (add (valof "n") (int -2)))))))
      (list (int 10))) null)
(int 55)

> (fri (?all (.. (true)
                (.. (?leq (false) (true))
                    (.. (?= (.. (int -19) (int 0))
                            (.. (head
                                (tail
                                  (tail (add (.. (int 1) (empty)) (.. (int 5) (.. (int -19) (empty)))))))
                                (int 0)))
                        (empty)))))
      null)
(true)

> (fri (vars (list "a" "b" "c")
              (list (int 1) (int 2) (int 3))
              (fun "linear" (list "x1" "x2" "x3")
                    (add (mul (valof "a") (valof "x1"))
                        (add (mul (valof "b") (valof "x2"))
                              (mul (valof "c") (valof "x3")))))) null)
(closure (list (cons "a" (int 1))(cons "b" (int 2)) (cons "c" (int 3)))
        (fun "linear" '("x1" "x2" "x3")
              (add (mul (valof "a") (valof "x1"))
                  (add (mul (valof "b") (valof "x2"))
                        (mul (valof "c") (valof "x3")))))))))

> (fri (handle (trigger (exception "fatal error"))
               (add (add (int 9) (int 9)) (int -1))
               (false))
       null)
(triggered (exception "fatal error"))

> (fri (add (int 1) (trigger (exception "fatal error"))) null)
(triggered (exception "fatal error"))

> (fri (trigger (exception "fatal error")) null)
(triggered (exception "fatal error"))

> (fri (add (add (int 9) (int 9)) (true)) null)
(triggered (exception "add: wrong argument type"))

> (fri (handle (exception "add: wrong argument type")
               (add (add (int 9) (int 9)) (true))
               (false))
       null)
(false)
> (fri (handle (exception "fatal error")
               (add (add (int 9) (int 9)) (true))
               (false))
       null)
(triggered (exception "add: wrong argument type"))
> (fri (handle (exception "fatal error")
               (add (add (int 9) (int 9)) (int -1))
               (false))
       null)
(int 17)
> (fri (handle (int 1337)
               (add (add (int 9) (int 9)) (int -1))
               (false))
       null)
(triggered (exception "handle: wrong argument type"))

3.2.9 “Glava” datoteke `02-project.rkt`

#lang racket

(provide false true int .. empty exception
         trigger triggered handle
         if-then-else
         ?int ?bool ?.. ?seq ?empty ?exception
         add mul ?leq ?= head tail ~ ?all ?any
         vars valof fun proc closure call
         greater rev binary filtering folding mapping
         fri)

3.2.10 Primer uporabe `racket/trace`

(require racket/trace)
(trace fri)
> (fri (?all (.. (true) (.. (?leq (false) (true))
                            (.. (?= (.. (int -19) (int 0))
                                    (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
                                (empty)))))
       null)
>(fri
  (?all
   (..
    (true)
    (..
     (?leq (false) (true))
     (..
      (?=
       (.. (int -19) (int 0))
       (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
      (empty)))))
  '())
> (fri
   (..
    (true)
    (..
     (?leq (false) (true))
     (..
      (?=
       (.. (int -19) (int 0))
       (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
      (empty))))
   '())
> >(fri (true) '())
< <(true)
> >(fri
    (..
     (?leq (false) (true))
     (..
      (?=
       (.. (int -19) (int 0))
       (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
      (empty)))
    '())
> > (fri (?leq (false) (true)) '())
> > >(fri (false) '())
< < <(false)
> > >(fri (true) '())
< < <(true)
< < (true)
> > (fri
     (..
      (?=
       (.. (int -19) (int 0))
       (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
      (empty))
     '())
> > >(fri
      (?=
       (.. (int -19) (int 0))
       (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)))
      '())
> > > (fri (.. (int -19) (int 0)) '())
> > > >(fri (int -19) '())
< < < <(int -19)
> > > >(fri (int 0) '())
< < < <(int 0)
< < < (.. (int -19) (int 0))
> > > (fri (.. (mul (add (int 1) (int 5)) (int -4)) (int 0)) '())
> > > >(fri (mul (add (int 1) (int 5)) (int -4)) '())
> > > > (fri (add (int 1) (int 5)) '())
> > > > >(fri (int 1) '())
< < < < <(int 1)
> > > > >(fri (int 5) '())
< < < < <(int 5)
< < < < (int 6)
> > > > (fri (int -4) '())
< < < < (int -4)
< < < <(int -24)
> > > >(fri (int 0) '())
< < < <(int 0)
< < < (.. (int -24) (int 0))
< < <(false)
> > >(fri (empty) '())
< < <(empty)
< < (.. (false) (empty))
< <(.. (true) (.. (false) (empty)))
< (.. (true) (.. (true) (.. (false) (empty))))
<(false)
(false)

3.2.11 Javni testi

Glej testno datoteko public-tests.rkt.

4 Izpiti

4.1 2024/25

4.1.1 2024/25 1. rok

24. 1. 2025

S sabo imate lahko 1 A4 list papirja z lastnimi zapiski, druga literatura (tiskane prosojnice, knjige) ni dovoljena. Vse naloge so enakovredne (po 10 točk), rešujte jih v predvidenem prostoru. Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate. Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 50 minut.

O nekem programskem jeziku vemo naslednje: Sistem izvaja zelo malo statičnih in dinamičnih preverjanj. Sintaksa jezika ne zahteva opredeljevanja podatkovnih tipov spremenljivk. V tem jeziku je razširjanje programske kode z novimi funkcijami preprosteje kot razširjanje z novimi podatkovnimi tipi.

Na katere tri lastnosti lahko sklepamo iz zgornjega opisa (poveži lastnosti z zgornjimi trditvami)?
- Šibka tipizacija: Sistem izvaja zelo malo statičnih in dinamičnih preverjanj.
- Implicitna tipizacija: Sintaksa jezika ne zahteva opredeljevanja podatkovnih tipov spremenljivk.
- Funkcijski sistem: V tem jeziku je razširjanje programske kode z novimi funkcijami preprosteje kot razširjanje z novimi podatkovnimi tipi.

Obkroži vse spremenljivke v telesu funkcije f, katerih vrednosti morajo biti nujno shranjene v optimizirani funkcijski ovojnici:

(define (f a d e)
   (+ (let ([b (* d 3)]) (+ b 1))
      (b d)
      (/ a e)))

(define (f a d e)
   (+ (let ([b (* d 3)]) (+ b 1))
      (|b|bg:orange| d)
      (/ a e)))

Podan je naslednji podatkovni tip:
```
datatype ('a, 'b, 'c) list = X of 'a * ('b, 'c, 'a) list | Stop
```
Zapiši primer izraza, za katerega velja, da:
- je zgornjega podatkovnega tipa,
- vsebuje uporabo petih konstruktorjev X,
- so tipi 'a, 'b in 'c med seboj različni.
```
X (1, X ("two", X (true, X (4, X ("five", Stop)))))
```
```
(* rezultat zgornjega izraza *)
val it = X (1,X ("two",X #)) : (int,string,bool) list
```
Razlaga:
- Podatkovni tip ('a, 'b, 'c) list z vsakim konstruktorjem X izmenično spreminja (rotira) tipske parametre.
- Vsak X uporablja drugačen tip za svoj element (int, string, bool, int, string), kar zagotovi, da parametri 'a, 'b, 'c ostanejo različni.
- Ugnezdene konstruktorje X ustvarijo 5-elementni seznam z zahtevano izmenjavo tipov skozi hierarhijo.
Podrobna razlaga podatkovnega tipa:
- Podatkovni tip ('a, 'b, 'c) list je trojno parametrizirana rekurzivna struktura, ki omogoča izmenjujoče elemente treh različnih tipov 'a, 'b in 'c v cikličnem vrstnem redu. Struktura ima dva konstruktorja:
  1. X of 'a * ('b, 'c, 'a) list
    - Vsak X vsebuje:
      
      Element tipa 'a (prvi parameter)
      
      Rep tipa ('b, 'c, 'a) list (ciklična rotacija parametrov: 'a → 'b → 'c → 'a).
  2. Stop
    - Končni element (analog nil v standardnem seznamu).
- Zgradba cikla
  
  Parametri se pri vsakem rekurzivnem klicu rotirajo:
```
('a, 'b, 'c) → ('b, 'c, 'a) → ('c, 'a, 'b) → ('a, 'b, 'c) → ...
```
- Primer
  
  Če imamo (int, string, bool) list, bo struktura izgledala takole:
```
X(1, X("two", X(true, X(4, X("five", X(false, Stop))))))
```
  Tipi elementov se ciklično menjajo:
  int → string → bool → int → string → bool → ...
- Zakaj je to uporabno?
  
  Takšna struktura je primerna za:
  - Modeliranje periodičnih sekvenc (npr. A → B → C → A → ...),
  - Zagotavljanje varnosti tipov pri cikličnih vzorcih.
- Značilnosti
  - Vsak element ima drugačen tip od predhodnika (rotirajoče),
  - Stop deluje ne glede na trenutno kombinacijo parametrov.

Podan je naslednji podatkovni tip:

datatype podatek = A of (int list) | B of {a:int, b:real} | C

Zapiši množico vzajemno rekurzivnih funkcij (toliko, kolikor jih je potrebnih), ki so podatkovnega tipa podatek list -> bool in preverijo, ali je vhodni seznam tak, da se v njem zaporedoma izmenjujejo elementi, ustvarjeni s konstruktorjema A in B. Prvi element seznama naj bo ustvarjen s konstruktorjem A.

Na primer:

Pravilni izrazi:

[A [1,2,3], B {a=1, b=1.0}, A [9,8,7], B {a=1, b=1.0}]
[A [1,2,3], B {a=1, b=1.0}]
[A [1,2,3]]

Nepravilni izrazi:

[A [1,2,3], B {a=1, b=1.0}, C]
[A [1,2,3], B {a=1, b=1.0}, B {a=1, b=1.0}]

fun is_valid [] = true (* če bi bil začetni vrstni red naključen *)
  | is_valid (A _ :: xs) = check_B xs
  | is_valid (B _ :: xs) = check_A xs
  | is_valid _ = false

and check_A [] = true
  | check_A (A _ :: xs) = check_B xs
  | check_A _ = false

and check_B [] = true
  | check_B (B _ :: xs) = check_A xs
  | check_B _ = false;

(rešitev preverjena s strani profesorja)

V jeziku SML sta podana modul in podpis. V podpisu so napake, zaradi katerih ni skladen z modulom, popravi jih. Podpis tudi spremeni tako, da je dosegljiv zgolj kontstruktor B.

structure Mod :> M2 = 
struct
   datatype podatek = A of int | B of real
   fun h1 (x,y) = 3 + y
   fun h2 (x,y) = 3 + y
   exception prazen
end

signature M2 = 
sig
   datatype podatek
   val h1: string * int -> int
   val h2: 'a * 'b -> 'c
end

signature M2 =
sig
   type podatek             (* dosegljiv samo B *)
   val B : real -> podatek
   val h1 : string * int -> int
   val h2 : 'a * int -> int    (* 'b je presplošen tip, zamenjamo z int *)
   (* exception ne dodamo v sig; le če bi bil v signature in ne structure, bi ga pa morali dodati v structure *)
end

(rešitev preverjena s strani profesorja)

Za spodnje izraze ugotovi, kateri imajo omejitev vrednosti in kateri ne. Argumentiraj v kratki povedi.

`val someVal = if true then (fn x=>1) else (fn x=>2)`	❌ OMEJITEV `val someVal = fn : ?.X1 -> int`
`val pair = (fn x => x, ref [])`	❌ OMEJITEV `val pair = (fn,ref []) : (?.X1 -> ?.X1) * ?.X2 list ref`
`val complex = (ref 0, fn x => x + 1)`	✅ NI OMEJITEV `val complex = (ref 0,fn) : int ref * (int -> int)`
`val x = List.map(fn x => x + 1);`	✅ NI OMEJITEV (delna aplikacija) `val x = fn : int list -> int list`
`val x = List.map (fn y => 14) [1, 2, 3]`	✅ NI OMEJITEV `val x = [14,14,14] : int list`
`val x = List.map (fn y => 14)`	❌ OMEJITEV (delna aplikacija) `val x = fn : ?.X1 list -> int list`

Utemeljitev: Deklaracije spremenljivk polimorfnih tipov dopustimo le, če je na desni strani vrednost (konstanta), spremenljivka ali nepolimorfna funkcija. To je omejitev vrednosti.

Kakšna je ključna razlika, vezana na način evalvacije, med naslednjima dvema izrazoma v programskem jeziku Python? Kateri izraz ima manjšo porabo spomina in zakaj?
```
[x*x for x in range(10)]
```
```
(x*x for x in range(10))
```
Prvi izraz takoj ustvari celoten seznam v spominu (eager evaluation), drugi izraz pa je generator in vrednosti vrača po eno ob dostopu (lazy evaluation), zato porabi manj spomina.

V Pythonu je podan naslednji izsek programske kode. Kakšen rezultat vrne klic v zadnji vrstici? Obkroži, katere vrednosti spremenljivk se upoštevajo pri računanju vsote x+y+z+u+v.

x=10
y=20
z=30
def pristej1(z=y):
   y=40
   def pristej2(y, v=y):
      print(x, y, z, u, v)
      return x+y+z+u+v  
   return pristej2
x = 12
y = 22
z = 32
u = 42
pristej1()(8,9)

x=10
y=20 # <--
z=30
def pristej1(z=y):
   y=40
   def pristej2(y, v=y):
      print(x, y, z, u, v) # 12 + 8 + 20 + 42 + 9
      return x+y+z+u+v  
   return pristej2
x = 12 # <--
y = 22
z = 32
u = 42 # <--
pristej1()(8,9)

Rezultat zadnje vrstice je 91.

4.2 2023/24

4.2.1 2023/24 1. rok

30. 1. 2024

S sabo imate lahko 1 A4 list papirja z lastnimi zapiski, druga literatura (tiskane prosojnice, knjige) ni dovoljena. Vse rešitve so enakovredne (po 10 točk), rešujte jih v predvidenem prostoru. Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša. Podpišite se na vse liste, ki jih oddate. Na vprašanja odgovarjajte kratko (največ 2 povedi). Daljši odgovori štejejo 0 točk.
Čas pisanja je 45 minut.

Razloži, kakšna je prednost funkcijskega programiranja, ki izvira iz idempotentnosti funkcij.

Idempotentne funkcije vedno vrnejo enak rezultat za iste vhodne podatke, ne glede na to kolikokrat jih kličemo. To omogoča lažje testiranje, boljšo predvidljivost delovanja in enostavnejše razhroščevanje programa.
V kateri paradigmi (funkcijsko programiranje ali objektno-usmerjeno programiranje) je preprostejše razširjanje z novimi funkcijami? Zakaj?

V funkcijskem programiranju je preprosteje dodajati nove funkcije, ker lahko enostavno definiramo nove funkcije, ki delujejo nad obstoječimi podatkovnimi tipi, ne da bi spreminjali obstoječo kodo. Pri OOP bi morali za nove funkcionalnosti pogosto modificirati obstoječe razrede.
Za nek tipizator vemo, da vedno razpoznava samo pravilno pozitivne in pravilno negativne primere programov. Kaj so 3 lastnosti tega tipizatorja, na katere lahko sklepaš na podlagi tega?
Tipizator je torej PP in PN.
1. Tipizator je trden - nikoli ne sprejme nepravilnega programa
2. Tipizator je poln - sprejme vse pravilne programe
3. Odločljivost (Decidability): (v tem kontekstu naj bi bilo isto kot ustavljiv) Tipizator vedno konča z odločitvijo (sprejme ali zavrne program) v končnem času. Ni primerov, kjer bi tipizator “obvisel” ali ne mogel dokončati analize.
// TODO: verify
Kakšen je postopek (oz. kakšne so faze) procesiranja vhodne izvorne kode, v kateri se nahajajo tudi definicije in uporabe makrov?
Postopek razširitve makro definicij (angl. macro expansion) se izvede pred prevajanjem in izvajanjem programa.
1. Leksikalna analiza - tokenizacija vhodne kode
2. Razširjanje makrojev (makro ekspanzija) - prepoznavanje in razširjanje makro definicij v osnovno SML kodo
3. Ponovna leksikalna analiza razširjene kode
4. Sintaksna analiza - gradnja abstraktnega sintaksnega drevesa
5. Semantična analiza in prevajanje
Določi podatkovni tip naslednji funkcije:
```
fun f a {a=b, b=c} =
   List.map (fn x=>a+(valOf b)-c(a))
```
```
val f = fn : int -> {a:int option, b:int -> int} -> 'a list -> int list
```
Razlaga:
1. Analiza parametrov:
  - Prvi parameter a je tipa int (določeno z uporabo +/-, ki privzeto delujeta s celimi števili v SML).
  - Drugi parameter je zapis (record) {a = b, b = c}:
  - b je vezan na polje a zapisa in ima tip int option (ker uporabljamo valOf b, ki razvije option tip).
  - c je vezan na polje b zapisa in mora biti funkcija tipa int -> int (ker c(a) sprejme celo število a in vrne celo število za odštevanje).
2. Vrni tip:
  - List.map je delno apliciran s funkcijo fn x => a + (valOf b) - c(a), ki ignorira svoj vhod x (tipa 'a). To ustvari funkcijo tipa 'a list -> int list.
Zaključni tip:

Funkcija f sprejme:
1. Celo število (int)
2. Zapis z zahtevanimi polji ({a: int option, b: int -> int})
3. Seznam poljubnega tipa ('a list) in vrne seznam celih števil (int list).
Navedi, kolikokrat se v spodnjem izrazu evalvira klic funkcije imenovane klic (utemelji v 1 povedi):
```
((let* ([rez (my-delay (lambda () (klic)))])
   (lambda () (+ (my-force rez) (my-force rez) (klic)))))
```
Funkcija klic se evalvira 2-krat: enkrat pri prvem klicu my-force rez (drugi my-force uporabi shranjeno vrednost) in enkrat pri direktnem klicu (klic). my-delay samo shrani lambda izraz, ne izvede ga.

V primeru, da ne bi bilo dodatnih zunanjih oklepajev bi se pa izvedlo 0-krat, saj bi Racket vrnil #<procedure>.

V jeziku SML je podan naslednji podatkovni tip:

datatype 'a podatek = A of int option list
                     | B of 'a option * {x:int}

Zapiši rekurzivne vzorce za case stavek, s katerimi lahko v neki rekurzivni funkciji seštejemo vsa cela števila, ki so podana v poljubnem izrazu e podatkovnega tipa string podatek list. Primer: V izrazu

[A [SOME 3, SOME 1, NONE, SOME 2], B (SOME "x", [x=5]), A [SOME 6]]

bi ta funkcija seštela 3+1+2+5+6 = 17.

Na spodnje črte zapiši samo rekurzivne vzorce, programske kode ni potrebno pisati:

case e of
   [] => 0
   ___ => (programska koda, nepotrebno zapisati)
   ___ => (programska koda, nepotrebno zapisati)
   ___ => (programska koda, nepotrebno zapisati)
   ___ => (programska koda, nepotrebno zapisati)

fun sumPodatek e =
   case e of 
      [] => 0 
      | (A ((SOME x) :: restA)) :: rest => x + sumPodatek ((A restA) :: rest)
      | (A (NONE :: restA)) :: rest => sumPodatek ((A restA) :: rest)
      | (B (_, {x})) :: rest => x + sumPodatek rest
      | _:: rest => sumPodatek rest;

Test:

val x = [A [SOME 3, SOME 1, NONE, SOME 2], B (SOME "x", {x=5}), A [SOME 6]];
sumPodatek(x);

V jeziku Racket zapiši kratko funkcijo (izpisi2 n tok), ki na vhodu prejme tok in število n ter izpiše vsak drugi element izmed prvih n elementov toka. Primer s tokom potence s predavanj:

> (izpisi2 5 potence) ; preskočimo izpis 4 in 16
2
8
32

(define potence            ; (list 2 4 8 16 32 64 128 256 512 ...)
   (letrec ([f (lambda (x)
      (cons x (lambda () (f (* x 2)))))])
                  (f 2)))

(define (izpisi2 n tok)
   (if (= (modulo n 2) 0)
      (if (= n 0)
         (void)
         (izpisi2 (- n 1) (cdr tok)))
      (begin
         (displayln (car tok))
         (izpisi2 (- n 1) (cdr tok)))))

> (izpisi2 5 potence)
2
8
32

V Pythonu je podan naslednji izsek programske kode. Kakšen rezultat vrne klic v zadnji vrstici? Obrazloži (1 poved).
```
x= 10
def pristej1(x):
   z=3
   def pristej2(y):
      return x+y+z
   z=5
   return pristej2
x=40
pristej1(10)(20)
```
Python uporablja dinamični scope.
1. pristej1(10) ustvari closure s shranjenim x=10 in z=5
2. pristej2(20) nato uporabi:
  - x=10 (iz closure)
  - y=20 (iz argumenta)
  - z=5 (iz closure, končna vrednost pred vrnitvijo pristej2)
3. Rezultat: 10 + 20 + 5 = 35

V jeziku SML napiši delno aplikacijo funkcije List.foldl, ki vrne terko dveh seznamov – tadva naj vsebujeta samo elemente na lihih oz. sodih zaporednih mestih seznama.

Primer:

Klic zgornje delne aplikacije na seznamu [6,1,3,8,3,4,6,3] vrne ([6,3,3, 6],[1,8,4,3]). Vrstni red seznamov v terki ni pomemben.

Odgovor:

(* ker je brez argumentov moramo dati val namesto fun *)
val lociSeznam =
     List.foldl (fn (x, (acc1, acc2)): (int * (int list * int list)) =>   (* pod. tipi so potrebni tukaj! *)
                    if length acc1 = length acc2 
                    then (acc1 @ [x], acc2) 
                    else (acc1, acc2 @ [x]))
                 ([], [])
                 (* delna aplikacija*)

> val rezultat = lociSeznam [6,1,3,8,3,4,6,3]
val rezultat = ([6,3,3,6],[1,8,4,3]) : int list * int list

4.2.2 2023/24 2. rok

13. 2. 2024

S sabo imate lahko 1 A4 list papirja z lastnimi zapiski, druga literatura (tiskane prosojnice, knjige) ni dovoljena. Vse naloge so enakovredne (po 10 točk), rešujte jih v predvidenem prostoru. Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša. Podpišite se na vse liste, ki jih oddate. Na vprašanja odgovarjajte kratko (največ 2 povedi).
Čas pisanja je 45 minut.

Za funkcijski klic v SML pojasni, kakšna so pravila za:
- preverjanje sintakse:
- semantiko pravilnosti podatkovnih tipov:
Sintaktična pravila:
- Funkcijski klic je sestavljen iz imena funkcije, ki mu sledijo argumenti
- Argumenti so lahko konstante, spremenljivke ali izrazi
- Oklepaji so opcijski (razen za eksplicitno določanje vrstnega reda)
Pravila za tipe:
- Število argumentov mora ustrezati številu parametrov v definiciji
- Tipi argumentov se morajo ujemati s tipi parametrov funkcije
- SML uporablja statično preverjanje tipov in inferenco tipov
- Funkcije so lahko polimorfne (sprejemajo različne tipe)
// TODO: verify

Funkcija povecaj je namenjena temu, da v vseh izrazih podatkovnega tipa, kot je naslednja vrednost b:

val b = [SOME (SOME 3, ref 10, {a=5}), SOME (NONE, ref 10, {a=5}), NONE]

poveča vse celoštevilske konstante za 1. V spodnji implementaciji funkcije povecaj manjkajo rekurzivni vzorci, dopolni jih.

fun povecaj e =
   case e of
      [] => []
      | _____________ => (SOME (SOME {a+1}, ref (b+1), {a=(c+1)}))::(povecaj r)
      | _____________ => (SOME (NONE, ref (b+1), {a=(c+1)}))::(povecaj r)
      | _____________ => NONE::(povecaj r)

fun povecaj e =
   case e of
      [] => []
      | SOME (SOME a, ref b, {a=c})::r => (SOME (SOME (a+1), ref (b+1), {a=(c+1)}))::(povecaj(r))
      | SOME (NONE, ref b, {a=c})::r => (SOME (NONE, ref (b+1), {a=(c+1)}))::(povecaj(r))
      | NONE::r => NONE::(povecaj(r))

Določi podatkovni tip naslednje funkcije:
```
fun h a b c =
   ref (List.filter a (List.map a b), c)

( _____ -> _____ ) -> ________ -> ________ -> __________
```
```
val h = fn : (bool -> bool) -> bool list -> 'a -> (bool list * 'a) ref
```
Razlaga:
- Prvi parameter a je funkcija tipa bool -> bool
- Drugi parameter b je seznam boolov bool list
- Tretji parameter c je poljubnega tipa 'a
- Rezultat je referenca na par (bool list * 'a) ref, kjer je prvi element seznam bool-ov, drugi pa vrednost tipa 'a
Denimo, da imata funkciji f1 in f2 isto programsko kodo, le da f1 uporablja currying, f2 pa ne. Zakaj je izvajanje druge hitrejše?
Razlika v hitrosti izvajanja med f1 (currying) in f2 (brez curryinga) izvira iz implementacije funkcijskega klica na nivoju strojne kode:

Pri curryingu (f1):
- Vsak delni klic funkcije zahteva:
- Alokacijo closure objekta v kopici (heap)
- Shranjevanje vrednosti prostih spremenljivk v closure
- Dodatne indirekcije pri dostopu do vrednosti
- Rezultat vsakega klica je nova funkcija
Brez curryinga (f2):
- En sam funkcijski klic
- Argumenti se prenesejo direktno preko sklada (stack)
- Ni potrebe po alokaciji closure objektov
- Ni dodatnih indirekcij pri dostopu do vrednosti
To se odraža v številu strojnih instrukcij in učinkovitosti upravljanja s pomnilnikom.
Kaj je razlika med eksplicitno in implicitno tipizacijo? Podaj po 2 primera programskih jezikov, ki uporabljata prvo in drugo.

Eksplicitna tipizacija zahteva, da programer sam določi podatkovne tipe spremenljivk in funkcij v programski kodi (Java, C++).

Pri implicitni tipizaciji prevajalnik sam ugotovi podatkovne tipe iz konteksta uporabe (type inference), kar programerju omogoča, da tipov ne piše eksplicitno (SML, Python).

Podani sta spodnji funkciji f1 in f2:

fun f1 a b = if a > 0 then a+b else a
fun f2 a b = if a < 10 then a*b else b

Dopolni programsko kodo funkcije višjega reda fx, ki sprejema dodatne funkcije g1, g2, g3 in g4, tako da bo s to funkcijo možno implementirati funkciji f1 in f2:

fun fx g1 g2 g3 g4 a b =
   if _____________ then _____________ else _____________

Zapiši novo implementacijo funkcije f1, imenovano f1x, ki z delno aplikacije funkcije fx izvaja enako nalogo kot originalna funkcija f1:

val f1x = fx _____________ _____________ _____________ _____________

f1:

pogoj: a > 0
če true: a+b
če false: a

f2:

pogoj: a < 10
če true: a*b
če false: b

Funkcija fx mora biti dovolj splošna, da lahko izrazi obe funkciji, zato:

fun fx g1 g2 g3 g4 a b =
   if g1 (g2 a b) then g3 a b else g4 a b;

Implementacija f1x z uporabo fx:

val f1x = fx
   (fn x => x > 0)           (* g1: preveri, ali je rezultat iz g2 > 0 *)
   (fn a => fn b => a)       (* g2: vrni `a`, da bo g1 preverjal `a > 0` *)
   (fn a => fn b => a + b)   (* g3: če je pogoj resničen, vrnemo `a + b` *)
   (fn a => fn b => a);      (* g4: če je pogoj neresničen, vrnemo `a` *)

alternativno:

fun fx g1 g2 g3 g4 a b =
   if g1 (g2 (a, b)) then g3 (a, b) else g4 (a, b);

val f1x = fx
   (fn x => x > 0)        (* g1: preveri, ali je rezultat iz g2 > 0 *)
   (fn (a, b) => a)       (* g2: vrni `a`, da bo g1 preverjal `a > 0` *)
   (fn (a, b) => a + b)   (* g3: če je pogoj resničen, vrnemo `a + b` *)
   (fn (a, b) => a);      (* g4: če je pogoj neresničen, vrnemo `a` *)

Obkroži vse spremenljivke v telesu funkcije f, katerih vrednosti morajo biti nujno shranjene v optimizirani funkcijski ovojnici:
```
(define a 1)
(define b 2)
(define (f a c d)
   (+ a b (let ([a b]) (+ a (let ([b 4]) (+ b c))))))
```
```
(define a 1)
(define b 2)
(define (f a c d)
   (+ a |b|bg:red|
      (let ([a |b|bg:red|])
         (+ a (let ([b 4])
            (+ b c))))))
```
Spremenljivke, ki jih je treba zajeti v optimizirano funkcijsko ovojnico, so b.

Razlaga:
1. Analiza dosega spremenljivk:
  - Funkcija f ima parametre a, c, d, ki zasenčujejo zunanje definicije teh imen.
  - Spremenljivka b v izrazu (+ a b ...) se nanaša na globalno spremenljivko b (vrednost 2), ker v tem delu kode ni lokalne definicije b v parametrih funkcije ali zunanjih let vezavah.
  - Poznejše let vezave (npr. ([a b]) in ([b 4])) ustvarjajo nove leksikalne dosege, vendar ne vplivajo na začetno sklicevanje na globalno b.
2. Identifikacija prostih spremenljivk:
  - b je edina spremenljivka v telesu funkcije f, ki ni niti parameter niti lokalno vezana. Je prosta spremenljivka, ki zahteva zajem v ovojnico.
  - Ostale spremenljivke (a, c) so bodisi parametri ali pa so zasenčene z lokalnimi vezavami.
Odgovor: V ovojnico je treba shraniti spremenljivko b.

Kakšen je rezultat naslednje vezave? Kratko pojasni, zakaj.

val f = let val a=1 in (fn _=>true) end;

> val f = let val a=1 in (fn _=>true) end;
stdIn:4.5-4.40 Warning: type vars not generalized because of
   value restriction are instantiated to dummy types (X1,X2,...)
val f = fn : ?.X1 -> bool

> (f)
val it = fn : ?.X1 -> bool

Koda	Rezultat	Razlaga
`val mojaf1 = map (fn x => 1)`	`mojaf1: ?.X1 list -> int list` Začasni tip; ne deluje pri uporabi	Omejitev vrednosti preprečuje generalizacijo zaradi takojšnjega vrednotenja izračuna.
`fun mojaf2 sez = map (fn x => 1)`	`mojaf2: 'a list -> int list` Polimorfično; deluje	Funkcije so obravnavane kot nespremenljive, zato je generalizacija dovoljena, s čimer se izognemo težavi z začasnim tipom.

V Pythonu je podan naslednji izsek programske kode. Kakšen rezultat vrne klic v zadnji vrstici? Obkroži, katere vrednosti spremenljivk se upoštevajo pri računanju vsote x+y+z+u+v.
```
x=10
y=20
def pristej1(z):
   u=3
   def pristej2(y, v=u):
      return x+y+z+u+v
   x=11
   y=21
   z=31
   u=41
   return pristej2
x = 12
y = 22
z = 32
u = 42
pristej1(1)(2)
```
Python uporablja dinamični doseg.

Rezultat klica pristej1(1)(2) je 88.

Spremenljivke, ki so upoštevane v vsoti x + y + z + u + v, so:
```
x=10
y=20
def pristej1(z):
   u=3 # <--
   def pristej2(y, v=u): # v=3, u=41
      return x+y+z+u+v
   x=11 # <--
   y=21
   z=31 # <--
   u=41 # <--
   return pristej2
x = 12
y = 22
z = 32
u = 42
pristej1(1)(2)
```
Razlaga vrednosti:
- x = 11 - iz lokalnega dosega pristej1
- y = 2- parameter funkcije pristej2
- z = 31 - iz lokalnega dosega pristej1
- u = 41 - posodobljena vrednost iz pristej1 (vpliva na izračun)
- v = 3- default parameter pristej2 (zajame začetno u=3 ob definiciji pristej2)

V jeziku SML sta podana modul in podpis. V podpisu so napake, zaradi katerih ni skladen z modulom, popravi jih. Podpis tudi spremeni tako, da je dosegljiv zgolj konstruktor A.

structure Mod :> M1 =         
struct                        
   datatype podatek = A of int | B of real   
   fun h1 x = 3               
end

signature M1 =
sig
   datatype podatek
   exception prazen
   val h1: 'a -> int
end

Popravljen podpis:

signature M1 =
sig
   type podatek
   val A: int -> podatek
   val h1: 'a -> int
end

4.3 2019/20

4.3.1 2019/20 1. rok

22. 1. 2020

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 10 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 60 minut.

NALOGA (10t):

Podaj odgovore na naslednji vprašanji (nalogi sta neodvisni):
1. (5t) Zapiši podatkovni tip naslednje funkcije:
```
fun x {a=b, c=d} h = 
   case (b,d) of 
      (SOME e, f::g) => e andalso f andalso (x {a=b, c=g} h )
      | (NONE, f::g) =>  f andalso (x {a=b, c=g} h)
      | _ => h
```
```
var x = fn: {a:bool option, c:bool list} -> bool -> bool
```
  Razlaga:
  1. Analiza zapisov (record):
    - Prvi parameter je zapis {a = b, c = d}.
    - b se primerja z SOME e in NONE, kar pomeni, da mora biti a tipa bool option (ker se e uporablja z andalso).
    - d se primerja z vzorcem f::g, f pa se uporablja z andalso, zato mora biti c tipa bool list.
  2. Drugi parameter h:
    - V privzetem primeru (_ => h) se vrne h, kar pomeni, da mora biti h tipa bool (saj mora ujemati tip rezultatov iz drugih vej).
  3. Vrsta vračane vrednosti:
    - Vse veje (ključevanje z case) vračajo logično vrednost (rezultat andalso ali h).
  Funkcija torej sprejme:
  - zapis s poljema a: bool option in c: bool list,
  - logično vrednost h,
  - in vrne logično vrednost (bool).
2. (5t) Izključno z uporabo funkcije List.foldl zapiši funkcijo find el sez, ki vrne zaporedna mesta vseh pojavitev iskanega elementa v podanem seznamu. Funkcija find naj uporablja currying. Primer delovanja:
```
- find 3 [1,3,3,6,3,4,2,3,54,3];
val it = [2,3,5,8,10] : int list
```
  Opomnik (podatkovni tip List.foldl):
```
fn : ('a * 'b -> 'b) -> 'b -> 'a list -> 'b
```
  Rešitev:
```
fun find el sez =
   #2 (List.foldl (
         fn (x, (i, acc)) => if x = el
                              then (i + 1, acc @ [i])
                              else (i + 1, acc))
      (1, [])
      sez)
```
  Razlaga:
  1. Indeksiranje z foldl:
    
    Uporabimo foldl, da hkrati štejemo indekse (začenši z 1) in zbíramo seznam pojavitev.
    
    Akumulator je par (i, acc), kjer je:
    - i trenutni indeks
    - acc seznam najdenih indeksov
  2. Dodajanje na konec seznama:
    
    Vsak nov najdeni indeks dodamo na konec seznama z acc @ [i].
  3. Delovanje na primeru:
    
    Za find 3 [1,3,3,6,3,4,2,3,54,3]:
    - Na indeksu 2 najdemo 3 → [2]
    - Na indeksu 3 najdemo 3 → [2,3]
    - Na indeksu 5 najdemo 3 → [2,3,5]
    - … in tako naprej.

NALOGA (10t):

V programskem jeziku SML je podan naslednji podatkovni tip:

datatype 'a inner = A of {a:'a} | B of 'a ref

Napiši funkcijo summarize, ki je podatkovnega tipa:

val summarize = fn : int inner option list -> {a:int, b:int}

Funkcija naj vrača zapis, ki hrani vsoto vrednosti elementov, ki so ustvarjeni s konstruktorjem A in vsoto vrednosti elementov, ki so ustvarjeni s konstruktorjem B. Primer delovanja:

val x1 = [SOME (A {a=3}),
          SOME (B (ref 5)),
          SOME (B (ref 5)),
          NONE,
          SOME (A {a=3}) ]

- summarize x1;
val it = {a=6,b=10} : {a:int, b:int}

datatype 'a inner = A of {a:'a} | B of 'a ref

val summarize = fn lst =>
   List.foldl (
      fn (opt, {a, b}) =>
         case opt of
            NONE => {a = a, b = b}
            | SOME (A {a = x}) => {a = a + x, b = b}
            | SOME (B r) => {a = a, b = b + !r}
      )
   {a = 0, b = 0}
   lst;

Na malo daljši način:

datatype 'a inner = A of {a:'a} | B of 'a ref

fun summarize sez =
   let
      fun in_summerize acc sez =
         let
            val {a, b} = acc (* ali kot: fun in_summerize {a=a, b=b} sez *)
         in
            case sez of
               nil => acc
               | NONE :: tail => in_summerize acc tail
               | SOME (A {a = x}) :: tail => in_summerize {a = a + x, b = b} tail
               | SOME (B (ref x)) :: tail => in_summerize {a = a, b = b + x} tail
         end
   in
      in_summerize {a=0, b=0} sez
   end;

NALOGA (10t):

V programskem jeziku Racket imamo podano funkcijo ifvsotafun, ki je implementirana na naslednji način:
```
(define (ifvsotafun e1 e2 e3 e4)
   (if (> (+ e1 e1) 30) (+ e2 e2 (e3)) (+ (e3) (e3) (e4) (e4) (e4))))
```
Odgovori na naslednja vprašanja:
1. (4t) Koliko najmanjkrat in največkrat se ob klicu funkcije evalvirajo spremenljivke e1, e2, e3 in e4?
  
  najmanjkrat največkrat
  
  e1
  
  e2
  
  e3
  
  e4
  
  najmanjkrat največkrat
  
  e1 1 1
  
  e2 1 1
  
  e3 1 2
  
  e4 0 3
  
  // TODO: improve razlago
  
  U funkciji se takoj k se ustvar ovojnica usi parametri evalvirajo 1 Tud ce se neuporabjo Edini razloz da ma e4 0 je zato ker je funkcija in funkcije se evalvirajo takrt k jih poklics Oziroma temu se rece zakasnjena evalvacija
  
  Ja pr makrotu se pa dobesedno sam prepisejo izrazi tkoda dobesedno veckrat izvajas isti izraz Pr ovojnici se pa k se ustvar ovojnica evalvirajo takoj enkrat in pol se uporablajo te izracunane vrednosti (razn ce je parameter funkcija pa je zakasnjena evalvacija)
  
  (define (ifvsotafun e1 e2 e3 e4) (if (> (+ e1 e1) 30) (+ e1 e1 (e3)) (+ (e3) (e3) (e4) (e4) (e4) e2))) Se prav kle bi bil e2: 1 1, tut ce ga v prvi veji neuporabmo
  
  Naprimr e3 pa e4 sta thunk funkciji k zgledata tko nekak (lambda () (+ 1 2))
  
  Pazi! To je za funkcijo, pri makroju je pa drugače.
2. (6t) Popravi funkcijo tako, da njeno telo oviješ v lokalno okolje, v katerem uporabi mehanizme za minimizacijo števila nepotrebnih evalvacij, kjer je to možno. Uporabiš lahko naslednje mehanizme (od najbolj preprostega do bolj zahtevnega): (1) lokalno okolje, (2) zakasnitvene funkcije, (3) zakasnitev in sprožitev. Za vsako spremenljivko uporabi najbolj preprost možen mehanizem od navedenih.
```
(define (ifvsotafun2 e1 e2 e3 e4)
   (let* ; Dopolni:
```
  // TODO:
```
(define (ifvsotafun e1 e2 e3 e4)
   (let* ([v3 (e3)])
         (if (> (+ e1 e1) 30)
               (+ e2 e2 v3)
               (let* ([v4 (e4)])
                  (+ v3 v3 v4 v4 v4)
               )
         )
   ))
```

	najmanjkrat	največkrat
e1	1	1
e2	1	1
e3	1	2
e4	0	3

NALOGA (10t):

V programskem jeziku Python napišite dekorator @arg_checker, ki preveri:

ali ima klicana funkcija natanko 2 pozicijska in 2 imenovana argumenta in
preveri, ali je med imenovanimi argumenti podan argument password z vrednostjo “koala”.

V primerjavi, da število argumentov ne ustreza, da ni podano geslo ali pa da je geslo napačno, naj (za vsakega od teh treh scenarijev) dekorator sporoči napako. V nasprotnem primeru naj dekorator izvede dekorirano funkcijo. Primer delovanja:

@arg_checker
def fun1(*args, **kwargs):
   return 42

>>> fun1(1, a=2)
'wrong number of parameters'
>>> fun1(1, 2, a=2, b=3)
'password not given'
>>> fun1(1, 2, a=2, password=3)
'password incorrect'
>>> fun1(1, 2, a=2, password="koala")
42

Namigi: Popolnoma točna sintaksa v Pythonu se ne ocenjuje. Kljub temu nekaj napotkov za lažje pisanje:

len(var) vrača dolžino polja ali slovarja,
key in kwargs.keys() preveri, ali je ključ vsebovan v slovarju,
kwargs[key] vrne vrednost ključa,
na razpolago so funkcije iz modula functools.

Odgovor:

def arg_checker(f):
   def wrapper (*args, **kwargs):
      if not (len(args) == 2 and len(kwargs) == 2):
         print("wrong number of parameters")
         return

      if not ("password" in kwargs.keys()):
         print("password not given")
         return

      if not (kwargs["password"] == "koala"):
         print("password incorrect")
         return

      return f(*args, **kwargs) # pazi da daš return, ker f vrača vrednost

   return wrapper

# Primer uporabe:
@arg_checker
def fun1(*args, **kwargs):
   return 42

# Test primeri:
fun1(1, a=2)
# 'wrong number of parameters'
fun1(1, 2, a=2, b=3)
# 'password not given'
fun1(1, 2, a=2, password=3)
# 'password incorrect'
fun1(1, 2, a=2, password="koala")
# 42

4.3.2 2019/20 2. rok

12. 2. 2020

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 10 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 60 minut.

NALOGA (10t):

V programskem jeziku Python sta podana dva razreda (sestavljena podatkovna tipa), ki predstavljata dve vrsti sadja:

class Jabolko:
   def teza(self):
      return 100

   def kalorije(self):
      return 80

class Hruska:
   def teza(self):
      return 150

   def kalorije(self):
      return 120

Nalogi:

(8t) S pomočjo relacije med objektno-usmerjenim in funkcijskim načinom programiranja, prevedi ta dva podatkovna v kodo programskega jezika SML.

datatype sadje = Jabolko
                 | Hruska

fun teza sad =
   case sad of
      Jabolko => 100
      Hruske => 150

fun kalorije sad = 
   case sad of
      Jabolko => 80
      Hruske => 120

Optimizirano:

datatype sadje = Jabolko 
                 | Hruska

fun teza Jabolko = 100
  | teza Hruska  = 150

fun kalorije Jabolko = 80
  | kalorije Hruska  = 120

(2t) V kateri od obeh paradigem je lažje razširjati število podatkovnih tipov (dodajati nove)?

Lažje je v objektno-usmerjenim, ker vse spremembe naredimo le na enem mestu (naredimo nov razred in implementiramo funkcije), medtem ko pri funkcijskem prog. moramo pri vsaki funkciji dodati nov case.

oz.

V objektno usmerjeni paradigmi je običajno lažje razširjati število podatkovnih tipov (dodajati nove), ker je mogoče preprosto definirati nove podrazrede, ki dedujejo obnašanje (metode) iz osnovnega razreda. Pri funkcijskem pristopu z algebrajskimi podatkovnimi tipi pa je tipično potrebno razširiti (in pogosto tudi preoblikovati) definicijo obstoječega tipa in vse funkcije, ki delajo z njim (uporabljajo pattern matching), kar lahko zahteva spremembe povsod v programu.

NALOGA (10t):

V programskem jeziku SML sta podani funkciji za izračun potence in vsote seznama, ki uporabljata repno rekurzijo:

fun potenca_repna (x,y) =
   let
      fun pomozna (x,y,acc) =
         if y=0
         then acc
         else pomozna(x, y-1, acc*x)
   in
      pomozna(x,y,1)
   end

fun vsota_repna sez =
   let
      fun pomozna (sez,acc) =
         if null sez
         then acc
         else pomozna(tl sez, acc+(hd sez))
   in
      pomozna(sez,0)
   end

Obe funkciji želimo posplošiti v novo, skupno funkcijo višjega reda repna_obdelava, za katero velja, da:

ima isto strukturo kot zgornji funkciji (lokalno okolje, vgrajeno pomožno funkcijo, if stavek, rekurzivni klic, klic pomožne funkcije),
ima prilagojen klic vgrajene pomožne funkcije (izberite argumente, ki so smiselni za posplošitev),
za dodatne argumente (potrebne za posploševanje) uporablja currying.

(6t) Zapiši posplošeno funkcijo repna_obdelava.

fun repna_obdelava f1 f2 f3 n vhod =
   let
      fun pomozna (vhod, acc) =
         if f1 (vhod)
         then acc
         else pomozna (f2(vhod), f3(vhod, acc))
   in
      pomozna (vhod, n)
   end

(4t) Zapiši delni aplikaciji posplošene funkcije, ki izvajata isto nalogo kot zgoraj podani funkciji.

val potenca_repna = repna_obdelava
                     (fn (x, y) => y=0)            (* f1 *)
                     (fn (x, y) => (x, y-1))       (* f2 *)
                     (fn ((x, y), acc) => acc*x)   (* f3 *)
                     1;                            (* zac. vr. *)

val vsota_repna = repna_obdelava
                     (fn sez => null sez)             (* f1 *)
                     (fn sez => tl sez)               (* f2 *)
                     (fn (sez, acc) => acc+(hd sez))  (* f3 *)
                     0;                               (* zac. vr. *)

NALOGA (10t):

V programskem jeziku Racket zapiši funkcijo preskocni_tok, ki sprejme:

poljubno število parametrov, ki predstavljajo elemente toka, ki se ciklično ponavlja,
opcijski imenovan parameter #:preskok, ki definira, koliko elementov (števši trenutnega) preskočimo do naslednjega elementa. Če argumenta ne podamo, naj ima privzeto vrednost 1 (kar pomeni, da jemljemo vedno naslednji element).

Funkcija naj vrne tok elementov, ki ustrezajo preskakovanju. Primeri delovanja (s funkcijo izpisi s predavanj):

> (izpisi 5 (preskocni_tok 1 2 3 4 5 6 7))    ; brez podanega parametra preskok
1
2
3
4
5
> (izpisi 5 (preskocni_tok 1 2 3 4 5 6 7 #:preskok 3))    ; s preskokom 3
1
4
7
3
6
> (izpisi 5 (preskocni_tok 1 2 3 4 5 6 7 #:preskok 6))    ; s preskokom 6
1
7
6
5
4

Neobvezna namiga: n-ti element v seznamu sez vrne funkcija (list-ref seznam n). Ostanek pri deljenju x z y se izračuna z (modulo x y).

Odgovor:

(define (preskocni_tok #:preskok [preskok 1] . args)
   (letrec ([f (lambda (x i)
                  (cons x (lambda () 
                     (f (list-ref args (modulo (+ i preskok) (length args)))
                        (modulo (+ i preskok) (length args))
                     )
                  ))
               )
            ])
      (f (car args) 0)
   )
)

> (izpisi 10 (preskocni_tok 2 3 5 7 11 13 17 #:preskok 3))
2
7
17
5
13
3
11
2
7
17

NALOGA (10t):

V programskem jeziku Python so podane naslednje definicije spremenljivk in funkcije:

a = 15
b = 13

def f1(x, y=a):
    def f2(a, c=b):
        return a + b + c
    return f2

V Pythonu nato izvedemo spodnje zaporedje klicev. Podaj odgovore Pythona (zapiši na črto) posameznih klicev (upoštevaj, da gre za zaporedje):

>>> f1(1)(3)
____
>>> f1(1)(3,4)
____
>>> f1(1,2)(3)
____
>>> f1(1,2)(3,4)
____
a = 25
b = 23
>>> f1(1)(3)
____
>>> f1(1)(3,4)
____
>>> f1(1,2)(3)
____
>>> f1(1,2)(3,4)
____

>>> f1(1)(3)
29 # 3 + 13 + 13
>>> f1(1)(3,4)
20 # 3 + 13 + 4
>>> f1(1,2)(3)
29 # 3 + 13 + 13
>>> f1(1,2)(3,4)
20 # 3 + 13 + 4
a = 25
b = 23
>>> f1(1)(3)
49 # 3 + 23 + 23
>>> f1(1)(3,4)
30 # 3 + 23 + 4
>>> f1(1,2)(3)
49 # 3 + 23 + 23
>>> f1(1,2)(3,4)
30 # 3 + 23 + 4

4.3.3 2019/20 1. kolokvij

26. 11. 2019

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 10 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 90 minut.

NALOGA (10t):

Reši spodnji podnalogi (med seboj sta neodvisni – nepovezani).
1. (6t) Določi podatkovni tip naslednje funkcije.
```
fun f1 (a,b,c::d) [i,j]  = 
   if c 
   then fn a => b (SOME i) 
   else fn b => a (j+1)
```
  Odgovor:
```
val f1 = fn: (int -> 'a) * (int option -> 'a) * bool list -> int list -> 'b -> 'a
```
  Razlaga:
  1. Vhodni parametri:
    - Prvi parameter: Trojček (a, b, c::d) s tremi komponentami:
    - a: Funkcija, ki sprejme celo število (int) in vrne vrednost poljubnega tipa 'a (tip: int -> 'a).
    - b: Funkcija, ki sprejme celo število v obliki option (int option, npr. SOME 5) in vrne 'a (tip: int option -> 'a).
    - c::d: Seznam logičnih vrednosti (bool list), kjer je c prvi element (tip bool), d pa preostanek seznama.
    - Drugi parameter: Seznam [i, j] z točno dvema elementoma (int list), kjer sta i in j celi števili (int).
  2. Logika funkcije:
    - Če je c true, vrne funkcijo fn a => b (SOME i).
    - Ta funkcija ignorira svoj parameter a (poljuben tip 'b) in kliče b z vrednostjo SOME i (tip rezultata: 'a).
    - Če je c false, vrne funkcijo fn b => a (j+1).
    - Ta funkcija ignorira svoj parameter b (poljuben tip 'b) in kliče a z vrednostjo j+1 (tip rezultata: 'a).
  3. Tip funkcije f1:
    - Vhod:
    - Trojček (int -> 'a) * (int option -> 'a) * bool list (prvi parameter).
    - Seznam int list (drugi parameter).
    - Izhod: Funkcija tipa 'b -> 'a (poljuben vhodni tip 'b, rezultat 'a).
2. (4t) Za naslednji izsek programske kode zapiši končno vrednost spremenljivk rez1 in rez2, glede na to, če bi kodo izvajali v leksikalnem ali dinamičnem dosegu:
```
val u = 1;
fun f v =
   fn w => u + v + w
val rez1 = (f 5) 6
val u = 3
val rez2 = (f 5) 6
```
  Odgovor:
  
  leksikalni doseg dinamični doseg
  
  rez1 =
  
  rez2 =
  
  leksikalni doseg dinamični doseg
  
  rez1 = 1+5+6=12 1+5+6=12
  
  rez2 = 1+5+6=12 3+5+6=14

	leksikalni doseg	dinamični doseg
rez1 =	1+5+6=12	1+5+6=12
rez2 =	1+5+6=12	3+5+6=14

NALOGA (10t):

(4t) Definiraj polimorfni podatkovni tip datatype ('a, 'b) chain, s katerim je možno oblikovati izraze naslednje oblike:

val izraz = Node({a=ref 15, b="pon"},
                  Node ({a=ref "tor", b = 12},
                        Node ({a=ref 42, b="sre"},
                              Node ({a=ref "cet", b=314},
                                    final))));

Pozor: podatkovna tipa prve in druge komponente v prvem izrazu konstruktorja Node se pri zaporednih elementih izmenjujeta.

Odgovor:

datatype ('a, 'b) chain = Node of 'a * ('b, 'a) chain
                        | final


datatype ('a, 'b) chain = Node of {a: 'a ref, b: 'b} * ('b, 'a) chain;
                        | final

// TODO: not working

(6t) Napiši funkcijo tipa

val chain_to_list = fn : ('a,'b) chain -> 'a list * 'b list

ki zgornji izraz obdela tako, da vrne elemente vsakega tipa ('a in 'b) v svojem seznamu. Pri funkciji uporabi rekurzivno ujemanje vzorcev (največ 1 globina stavka case in izogibanje zaporednemu naslavljanj terk s sintakso #1, #2 itd.). Ne uporabljaj vgrajenih funkcij višjega reda (map/filter/fold). Primer delovanja:

- chain_to_list izraz;
val it = ([15,12,42,314],["pon","tor","sre","cet"]) : int list * string list

Odgovor:

fun chain_to_list c =
   let
      fun pomozna final _ = ([], [])
        | pomozna (Node(x, xs)) flag =
            let
               val (as_list, bs_list) = pomozna xs (not flag)
            in
               if flag then
               (* Pri lihem položaju: x je tipa {a: int ref, b: string} *)
               ((!(#a x)) :: as_list, (#b x) :: bs_list)
               else
               (* Pri sodem položaju: x je tipa {a: string ref, b: int} *)
               ((#b x) :: as_list, (!(#a x)) :: bs_list)
            end
   in
      pomozna c true
   end;

// TODO: not working

      fun chain_to_list sez =
   let
      fun pomozna sez (a, b) flip =
         case sez of
            final => (a, b)
            | Node (x) :: rest => 
               if flip
               then pomozna rest (a @ [x], b) false
               else pomozna rest (a, b @ [x]) true
   in
      pomozna sez ([], []) true
   end

NALOGA (10t):

Podan je naslednji modul (structure) za delo z izgralnimi kartami:

structure Karte  =
struct
   (* podatkovni tipi za predstavitev igralnih kart in množice kart v rokah *)
   datatype barva = Pik | Karo | Srce | Kriz
   datatype karta = Karta of (barva * int) | Joker
   type karte = string list

   (* seznam kart, ki jih držimo v rokah, val v_roki : karte ref *)
   val v_roki = ref []:karte ref

   (* izjema, ki se proži ob izdelavi primerka neveljavne karte *)
   exception NeveljavnaKarta of (barva * int)

   (* funkcija za izdelavo primerka nove karte, val nova_karta : barva * int -> karta *)
   fun nova_karta (barva, int) =
      if (int>=2 andalso int <=14) then Karta(barva,int) else raise NeveljavnaKarta(barva,int)

   (* funkcija za dodajanje nove karte v roke, val dodaj_v_roke : karta -> karte *)
   fun dodaj_v_roke (nova:karta) =
      let val count_jokers = List.foldl (fn (el,ac)=>if (el="Joker") then ac+1 else ac) 0 (!v_roki)
      in
         (case nova of
               Joker => if (count_jokers <4) then v_roki := (!v_roki) @ ["Joker"] else ()
            | _ => v_roki := (!v_roki) @ ["Karta"]
         ; (!v_roki))
      end

   (* prikaže karte, ki jih imamo v rokah,  val pokazi_roke : unit -> karte *)
   fun pokazi_roke () = (!v_roki)
end

Naloga: Zapiši najkrajši možen podpis za zgornji modul, ki zagotavlja, da lahko uporabnik izvaja naslednje:

ima vpogled v svoje karte, ki jih ima v roki,
lahko v karte v roki doda novo karto tipa karta (oba podtipa: Karta ali Joker),
doda lahko le veljavno karto podtipa Karta (številka karte v ustreznih mejah).

Odgovor:

signature KarteK =
sig
   datatype barva = Pik | Karo | Srce | Kriz
   datatype karta = Karta of (barva * int) | Joker
   type karte

   exception NeveljavnaKarta of (barva * int)

   val v_roki : karte ref
   val nova_karta : barva * int -> karta
   val dodaj_v_roke : karta -> karte
   val pokazi_roke : unit -> karte
end

// TODO: verify

NALOGA (10t):

V programskem jeziku SML so podane naslednje tri funkcije, ki uporabljajo vzajemno rekurzijo:
```
fun first_op sez =
   case sez of
      nil => [true]
      | g::r => (not g)::(second_op r)
and second_op sez =
   case sez of
      nil => [false]
      | g::r => (g)::(third_op r)
and third_op sez =
   case sez of
      nil => nil
      | g::r => true::(first_op r)
```
Naloge:
1. (8t) Refaktoriziraj (nadomesti/združi) zgornje tri funkcije v eno samo splošnejšo funkcijo višjega reda z imenom op123, ki lahko izvaja delovanje poljubne izmed treh zgornjih funkcij. Posplošena funkcija op123 naj ima enako ogrodje kot zgornje tri funkcije, razlikuje pa se lahko samo na mestih, kjer obstajajo med njimi razlike. Na teh mestih za posplošitev uporabi ustrezne dodatne parametre (funkcije višjega reda). Funkcija naj uporablja currying.
```
fun op123 ifNil funH funT sez =
   case sez of
      nil => ifNil
      | g::r => (funH g)::(funT r)
```
  ali:
```
fun op123 ifNil _ _ [] = ifNil
  | op123 ifNil funH funT (g::r) = (funH g)::(funT r)
```
2. (2t) Zapiši aplikacijo funkcije op123, ki implementira enako delovanje zgornji funkciji first_op.
```
fun first_op sez =
   op123 [true] (fn x => not x) second_op sez;
```

4.3.4 2019/20 2. kolokvij

14. 1. 2020

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 10 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 60 minut.

NALOGA (10t):

Podana sta dva programa, P1 in P2, ki imata sintaktične in semantične napake. Nad P1 in P2 poženemo nek prevajalnik. Kaj lahko sklepaš o trdnosti/polnosti prevajalnika in o uvrstitvi programov P1 in P2 med pravilno pozitivne, lažno pozitivne, pravilno negativne in lažno negativne (kategoriziraj v: PP, LP, PN, LN) v naslednjih primerih?
1. Prevajalnik sprejme (uspešno prevede) P1 in zavrne P2.
  
  Prevajalnik:
  
  P1:
  
  P2:
  
  Prevajalnik: Lahko sklepamo, da je poln, ker trden prevajalnik nima LN programov.
  
  P1: LN
  
  P2: PP
2. Prevajalnik zavrne oba – P1 in P2.
  
  Prevajalnik:
  
  P1:
  
  P2:
  
  Prevajalnik: Ne moremo vedeti, premalo informacij.
  
  P1: PP
  
  P2: PP
3. Prevajalnik sprejme oba programa – P1 in P2.
  
  Prevajalnik:
  
  P1:
  
  P2:
  
  Prevajalnik: Lahko sklepamo, da je poln, ker trden prevajalnik nima LN programov.
  
  P1: LN
  
  P2: LN
4. Prevajalnik se pri vsaj enem vhodu nikoli ne ustavi (ne vrne odgovora).
  
  Kaj lahko sklepaš glede njegove trdnosti in polnosti, če predpostavimo, da problem neustavljivosti izhaja iz neupoštevanja neodločljivosti istočasne izpolnjenosti vseh treh zaželenih pogojev statične analize?
  
  Prevajalnik:
  
  Prevajalnik: Neustavljivost pri nekaterih vhodih kaže, da ni dosegljiva popolna odločljivost. To pomeni, da poskuša hkrati zagotoviti trdnost in polnost – kar pa je zaradi neodločljivosti statične analize teoretično nemogoče. Zato se lahko sklepa, da prevajalnik (čeprav morda uresničuje eno lastnost) ne more biti hkrati trden in poln, kar se manifestira v nekaterih vhodih s neustavljivostjo.
  
  // TODO: verify d)
NALOGA (10t):

V programskem jeziku Racket sprogramiraj funkcijo (unpack fun), ki na vhodu sprejme funkcijo fun in generira tok (stream), kot je opisano v nadaljevanju. Funkcija fun naj ustreza pogojem, da je brez argumentov in uporablja currying tako, da so tudi vse vgnezdene funkcije brez argumentov, npr.:
```
(define f1
   (lambda ()
      (lambda ()
         (lambda ()
            (lambda ()
               (+ 3 2))))))
```
Generiran tok naj v posameznih elementih vsebuje naslednjo notranjo funkcijo prvotno podane funkcije, vse dokler ne pride do končnega rezultata. Takrat naj se elementi toka (končna izračunana vrednost) začnejo ponavljati. Primer delovanja na zgornji funkciji fun (uporabljena je funkcija izpisi s predavanj, ki izpiše prvih 10 elementov toka):
```
> (izpisi 10 (unpack f1))
#<procedure:fun>
#<procedure:...2019-20-kol1.rkt:5:4>
#<procedure:...2019-20-kol1.rkt:6:6>
#<procedure:...2019-20-kol1.rkt:7:8>
5
5
5
5
5
5
```
Namig: Pri izdelavi lahko uporabite predikat (procedure? f), ki vrne #t, če je f funkcija, sicer pa #f.

// TODO:
NALOGA (10t):

V programskem jeziku Racket želimo implementirati makro ifvsota, ki nadomešča vgrajeni if stavek:
```
(define-syntax ifvsota
   (syntax-rules ()
      [(ifvsota e1 e2 e3 e4)
         (if e1 (+ e2 e2 e3) (+ e3 e3))]))
```
Odgovori na naslednja vprašanja:
1. (4t) Koliko najmanjkrat in največkrat se ob klicu makra evalvirajo spremenljivke e1, e2, e3 in e4?
  
  najmanjkrat največkrat
  
  e1
  
  e2
  
  e3
  
  e4
  
  najmanjkrat največkrat
  
  e1 1 1
  
  e2 0 2
  
  e3 1 2
  
  e4 0 0
  
  Argumenti makroja se evalvirajo šele ob klicu, ne ob definiciji.
2. (6t) Popravi le zadnjo vrstico zgornjega makra (napiši novi makro ifvsota2, ki vrača enak rezultat kot makro ifvsota) tako, da v razvito programsko kodo dodaš mehanizme za minimizacijo števila nepotrebnih evalvacij, kjer je to možno. Uporabiš lahko naslednje mehanizme (od najbolj preprostega do bolj zahtevnega): (1) lokalno okolje, (2) zakasnitvene funkcije, (3) zakasnitev in sprožitev. Za vsako spremenljivko uporabi najbolj preprost možen mehanizem od navedenih.
```
(define-syntax ifvsota2
   (syntax-rules ()
      [(ifvsota2 e1 e2 e3 e4)
         ; Dopolni:
```
```
(* Lokalno okolje, najslabša rešitev *)
(if e1
   (letrec ([d2 (e2)]
            [d3 (e3)])
            (+ d2 d2 d3))
   (letrec ([d3 (e3)])
            (+ d3 d3)))

(letrec ([ev3 e3]
         [ev2 e2])
         (if e1 (+ ev2 ev2 ev3) (+ ev3 ev3)))

(* Najtežja rešitev z zakasnitvami in sprožitveni *)
(letrec ([ev3 e3]
         [d2 (delay (lambda () e2))])
         (if e1 (+ (force d2) (force d2) ev3) (+ ev3 ev3)))
```
NALOGA (10t):

Podana je definicija funkcije prva, ki uporablja currying z vgnezdenimi funkcijami druga in tretja:
```
1  (define a 3)
2  (define (prva b c)
3    (let* ([c (+ 12 a)]
4           [druga (lambda (a)
5                    (let* ([tretja (lambda ()
6                                      (+ a b c))])
7                       tretja))])
8      druga))
```
Naloge:
1. (2t) Zapiši sintaktično pravilen primer klica zgornje funkcije, ki izvede seštevanje treh argumentov v funkciji tretja. V zapisanem primeru sam/a izberi poljubne vrednosti dejanskih argumentov. Zapiši tudi rezultat tega funkcijskega klica.
```
(((prva 10 20) 30)) ; oklepaji so pomembni!
55 ; a + b + c: 30 + 10 + (12+3)
```
2. (8t) Funkcijam prva, druga in tretja želimo optimizirati vsebino funkcijskih ovojnic in v njih ohraniti le spremenljivke, ki so nujno potrebne. Za vsako od treh funkcij navedi, katere spremenljivke so to (podaj ime spremenljivke in vrstico, v kateri se nahaja (glej številčenje vrstic na levi strani).
  
  prva: ____
  
  druga: ____
  
  tretja: ____
  prva: a: 3. vrstica
  
  druga: b, c: 6. vrstica
  
  tretja: a, b, c: 6. vrstica
  
  Razlaga:
  - Pri prva rabiš sam a, ker sta b in c podana kot argumenta.
  - Pri druga rabiš b in c, ker se uporabita v tretja, vendar a ne rabiš, ker je podan kot argument.
  - Pri tretji rabiš a, b in c.

	najmanjkrat	največkrat
e1	1	1
e2	0	2
e3	1	2
e4	0	0

4.4 2018/19

4.4.1 2018/19 1. rok

23. 1. 2019

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 5 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 50 minut.

NALOGA (5t):

Na kratko (največ dve povedi!) odgovori na naslednja vprašanja:
1. (1t) Kaj je pomanjkljivosti sistema tipov (tipizator), ki je hkrati poln in trden?
  
  Če je hkrati trden in poln, ni ustavljiv (izbiramo lahko namreč le 2 od 3 opcij).
2. (1t) Kombinacija dveh funkcionalnosti programskega jezika vodi do težav pri statičnem sistemu tipov, ki se jih prevajalnik lahko ogne z omejitvijo vrednosti. Kateri dve funkcionalnosti sta to?
  
  Šibko tipiziranje, polimorfizem.
3. (1t) Kako lahko zmanjšamo odvečno število evalvacij, če namesto funkcije generiramo kodo z makrom?
  
  Lahko uporabimo lokalno okolje in v njem evalviramo izraz, lahko evalvacijo zakasnimo (tako lahko tudi na primer preprečimo neskončno rekurzijo) ali pa uporabimo metodo “zakasnitev - sprožitev”, kar je vedno najbolj učinkovito (ne pa najbolj enostavno).
4. (2t) Kakšen je podatkovni tip funkcije f?
```
fun f x y z = List.foldl (fn (g1::g2::r, y) => SOME(g2+(valOf y)))
```
```
val f = fn: 'a -> 'b -> 'c -> int option -> int list list -> int option

(* notranja fn: (int list * int option) -> int option *)
```

NALOGA (5t):

V programskem jeziku SML želimo graditi drevesne izraze oblike Node(levo_drevo, element, desno_poddrevo). Želimo, da drevo na lihih nivojih hrani elemente prvega podatkovnega tipa, na sodih nivojih pa elemente drugega. Primeri izrazov:

- Node(fin,1,fin);
val it = Node (fin,1,fin) : (int,'a) node

- Node(fin,1,Node(fin,true,Node(fin,4,fin)));
val it = Node (fin,1,Node (fin,true,Node (fin,4,fin))) : (int,bool) node

- Node(Node(fin,true,fin),1,Node(fin,true,Node(fin,4,fin)));
val it = Node (Node (fin,true,fin),1,Node (fin,true,Node (fin,4,fin))) : (int,bool) node

- Node(Node(fin,true,fin),1,Node(fin,true,Node(fin,false,fin)));
stdIn:1.2-6.14 Error: operator and operand don't agree [overload conflict]
   operator domain: (bool,[int ty]) node * [int ty] * (bool,[int ty]) node
   operand:         (bool,[int ty]) node * [int ty] * (bool,bool) node

Naloge:

(2t) Zapiši definicijo podatkovnega tipa, s katerim je možno zapisati zgornje izraze.

datatype ('a, 'b) node = Node of ('b, 'a) node * 'a * ('b, 'a) node
                        | fin;

(3t) Zapiši funkcijo za izračun višine drevesa (pozor, namig: običajna rekurzivna funkcija za spust po drevesu ne deluje, zakaj?). Primeri:

- height (Node(fin,1,Node(fin,true,fin)));
val it = 2 : int
- height (Node(fin,1,Node(fin,true,Node(fin,4,fin))));
val it = 3 : int

fun height t =
   let
      (* h1 obdeluje vozlišča, kjer je element tipa 'a (neparni nivoji) *)
      fun h1 fin = 0
        | h1 (Node(l, _, r)) = 1 + Int.max (h2 l, h2 r)
      (* h2 obdeluje vozlišča, kjer je element tipa 'b (sodi nivoji) *)
      and h2 fin = 0
        | h2 (Node(l, _, r)) = 1 + Int.max (h1 l, h1 r)
   in
      h1 t
   end;

Samo:

fun height fin = 0
  | height (Node(l,_,r)) = 1 + Int.max (height l, height r);

pa ne bo tipno ustrezal, ker funkcija height pričakuje argumente tipa ('a, 'b) node, v rekurzivnih klicih pa dobimo vrednosti tipa ('b, 'a) node.

NALOGA (5t):

Podan je okrnjen interpreter za JAIS (jais3), ki smo ga začeli izdelovati na predavanjih. Interpreter ima že sprogramirano shranjevanje imenovanih spremenljivk (shrani) in dostop do njih (beri).

(struct konst (int) #:transparent)                 ; konstanta; argument je število 
(struct sestej (e1 e2) #:transparent)              ; e1 in e2 sta izraza 
(struct shrani (ime vrednost izraz) #:transparent) ; shrani spremeljivko z imenom ime 
   (struct beri (ime) #:transparent)               ; bere spremenljivko z imenom ime

(define (jais3 e)  
   (letrec ([jais (lambda (e env)
            (cond [(konst? e) e]   ; vrnemo izraz v ciljnem jeziku 
                  [(nic? e) e] 
                  [(par? e) e] 
                  [(shrani? e) (jais (shrani-izraz e)  
                                    (cons (cons (shrani-ime e) (jais (shrani-vrednost e) env)) 
                                 env))] 
                  [(beri? e) (cdr (assoc (beri-ime e) env))] 
                  [(sestej? e) |… koda za seštevanje s predavanj (pokrajšano)…|bg:gray|
                     [#t (error "sintaksa izraza ni pravilna")]))]) 
      (jais e null)))

Naloge:

(1t) Zapiši strukturi par in nic (zgornji interpreter že vsebuje kodo zanju), s katerima je možno definirati pare in z njihovim gnezdenjem oblikovati sezname. Primer:

> (jais3 (par (konst 1) (par (konst 2) (par (konst 3) (nic)))) 
(par (konst 1) (par (konst 2) (par (konst 3) (nic))))

Rešitev:

(struct par (e1 e2) #:transparent)
(struct nic () #:transparent)

(4t) Zapiši strukturo moj-let*, ki sprejme seznam vezav (narejen z gnezdenjem strukture par) in izraz. Moj-let* naj evalvira podani izraz v lokalnem okolju podanih vezav na enak način, kot izvaja Racket evalvacijo pri tvorjenju lokalnega okolja s stavkom let*. Torej, kljub že definiram spremenljivkam (v spodnjem primeru a z vrednostjo 2), moj-let* evalvira podane vezave zaporedno. Pri vsaki evalvaciji sproti razširi okolje z novo vezavo in jo upošteva pri nadaljnjih vezavah (zato b dobi vrednost spremenljivke a, ki je prva v zaporedju vezav). Primer:

> (jais3 (shrani "a" (konst 2)  
         (moj-let* (par (par "a" (konst 3)) (par (par "b" (beri "a")) (nic)))  
         (sestej (beri "a") (beri "b"))))
(konst 6)

Rešitev:

;; moj-let*: evalvira vezave zaporedno, kot pri let* 
[(moj-let*? e)
   (let* ([bindings (moj-let*-bindings e)]
          [izraz    (moj-let*-izraz e)])
   ;; Funkcija, ki zaporedno evalvira vezave.
   (define (eval-bindings bs env0)
      (cond
         [(nic? bs) env0]
         [(par? bs)
         (let* ([binding (par-prvi bs)]
               [ostalo  (par-drugi bs)])
            (unless (par? binding)
            (error "moj-let*: nepravilna vezava" binding))
            (let* ([var  (par-prvi binding)]
                  [vexp (par-drugi binding)]
                  [vred (jais vexp env0)])
            (eval-bindings ostalo (cons (cons var vred) env0))))]
         [else (error "moj-let*: nepričakovana struktura vezav" bs)]))
   (jais izraz (eval-bindings bindings env)))]

// TODO: verify

NALOGA (5t):

Samo z uporabo funkcije List.foldl zapiši funkcijo fun poz flist arg limit, katere argumenti pomenijo:
- flist: seznam funkcij (vse naj sprejemajo natanko 1 argument),
- arg: dejanski parameter (argument), s katerim kličemo funkcije s seznama flist,
- limit: meja, s katero primerjamo rezultat funkcij.
Funkcija poz naj vrne število funkcij s seznama flist, ki ob klicu z argumentom arg vrnejo rezultat, ki je večji ali enak vrednosti limit. Primer:
```
- poz [fn x => x+3, fn x => 2*x] ~2 0;       (* od 1 in -4 je samo 1 >= 0 *) 
val it = 1 : int 

- poz [fn x => x+3, fn x => 2*x] ~2 ~10;     (* od 1 in -4 sta obe >= -10 *) 
val it = 2 : int 
```
Opomnik: List.foldl: fn : ('a * 'b -> 'b) -> 'b -> 'a list -> 'b

Rešitev:
```
fun poz flist arg limit =
   List.foldl
      (fn (flistX, acc) => if flistX(arg) >= limit
                           then acc+1
                           else acc)
      0
      flist;
```

4.4.2 2018/19 2. rok

13. 2. 2019

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna označeno število točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 50 minut.

NALOGA (4t):

Na kratko (največ dve povedi!) odgovori na naslednja vprašanja:
1. (1t) Imejmo sistem tipov (tipizator), ki je poln in trden? Zakaj tak tipizator v praksi ni uporaben?
  
  Če je hkrati trden in poln, ni ustavljiv (izbiramo lahko namreč le 2 od 3 opcij).
2. (1t) Minimalno katere lastnosti mora programski jezik oz. njegov sistem tipov (tipizator), da lahko brez uvedbe posebnih novih podatkovnih tipov implementiramo sezname, ki hranijo elemente različnih tipov (kot npr. v Pythonu ali Racketu)?
  
  Dinamično tipiziranje: Vsaka vrednost nosi s seboj informacijo o svojem tipu in preverjanje tipov se opravi ob izvajanju.
  
  ali
  
  Polimorfne podatkovne tipe.
3. (2t) Določite podatkovni tip naslednjima funkcijama, zapisanima v jeziku SML. Ugotovite morebitno težavo (ilustrirajte jo s primerom) in opišite, kakšno pomoč vam v tem primeru nudi prevajalnik SML:
```
fun f1(SOME a) = f2(valOf a)
and f2(b)      = 2*b;
```
```
val f1 = fn: int option option -> int
val f2 = fn: int -> int
```
  Morebitna težava: Če bi podali v f1 recimo string option option, bi še vedno šlo v naslednji korak - bi klicalo funkcijo f2, kjer bi se zataknilo, ker stringa ne moremo množiti z int. Prevajalnik nam že po prevajanju izpiše, kakšnega tipa morajo biti argumenti. Če podamo napačne, nam vrne napako.
  
  // TODO: improve težava
NALOGA (6t):

V programskem jeziku SML želimo imamo implementirani funkciji F in G na naslednji način:
```
fun F 0 b = 0 
  | F a b = b + F (a-1) b;

fun G a 0 = 1 
  | G a b = F a (G a (b-1));
```
Naloge:
1. (1t) Izračunajte F 4 5 in G 2 10
  - F:
    1. F 4 5
    2. 5 + F 3 5
    3. 5 + F 2 5
    4. 5 + F 1 5
    5. 5 + F 0 5
    6. 0
    Rezultat: $4*5 = 20$
  - G:
    1. G 2 10
    2. F 2 (G 2 9) -> F 2 (F2 (G 2 8)) -> … -> F 2 (F 2 … (G 2 0)) -> F 2 1
    3. 1 + F (1, 1)
    4. 1 + F (0, 1)
    5. 2
    6. F (2, 2)
    7. 2 + F (1, 2)
    8. 2 + F (0, 2)
    9. 4
    10. F (2, 4)
    …
    
    Rezultat: $2^{10} = 1024$
2. (1t) Opišite, kaj zares delata funkciji F in G.
  
  F = a * b: F množi z rekurzijo.
  
  G = a ^ b: G potencira z rekurzijo.
3. (1t) Ali je katera od omenjenih funkcij vzajemno rekurzivna? Če da, opišite zakaj!
  Ne, funkciji nista medsebojno/vzajemno rekurzivni.
  - Funkcija F kliče sama sebe in ni odvisna od funkcije G.
  - Funkcija G sicer kliče sama sebe (v primeru G a (b-1)) in poleg tega kliče funkcijo F, vendar F ne kliče G.
  Za vzajemno rekurzijo bi morali imeti krog, kjer ena funkcija kliče drugo, ki nato kliče nazaj prvo. Tu tega ni.
4. (1t) Ali je katera od omenjenih funkcij repno rekurzivna? Če da, jo navedite, če ne, pa opišite, zakaj ne.
  
  Nobena ni, ker oboji funkcijski klici povzročijo kreiranje nove funkcijske ovojnice oz. se argumenti gnezdijo kot funkcije.
5. (2t) Če lahko, funkciji F in G pretvorite v repno rekurzivno obliko. Če ne, argumentirajte, zakaj ne.
```
fun F a b =
   let
      fun pomozna (0, acc) = acc
        | pomozna (a, acc) = pomozna (a-1, acc + b)
   in
      pomozna (a, 0)
   end;
```
```
fun G a b =
   let
      fun pomozna (0, acc) = acc
        | pomozna (b, acc) = pomozna (b-1, F a acc)
   in
      pomozna (b, 1)
   end;
```
NALOGA (5t):

V programskem jeziku Racket bi radi implementirali ekvivalent funkcije višjega reda fold, ki bi omogočal izvajanje te operacije nad tokovi. Okvirna sintaksa definicije:
```
(define (fold/stream func acc stream) …)
```
1. (1t) Samo ena od različic običajne funkcije fold je smiselna za tokove. Katera in zakaj?
  
  Smiselna je foldl. Razlog je, da se pri tokovih elementi generirajo “na zahtevo” in je dostop do naslednjega elementa možen šele, če že obdelamo prejšnjega. Pri foldl se akumulator posodablja od leve proti desni, kar ustreza naravi tokov. Po drugi strani pa foldr zahteva rekurzijo “od desne proti levi” (kar vključuje neobstoječi “konec” neskončnega toka) in zato ni primerna za delo s tokovi.
2. (1t) Gornjo okvirno definicijo je iz praktičnih razlogov potrebno dopolniti z dodatnim argumentom. Katerim in zakaj?
  
  Dodaten argument v akumulatorju bi bilo število, kolikokrat naj se fold izvede nad tokom.
  
  Alternativna rešitev:
  
  Pri rednih seznamih lahko za prekinitev folda uporabimo že definirani test (null? stream). Pri tokovih pa ni nujno, da je “praznina” (konec) tokov enostavno prepoznana, saj so tokovi pogosto definirani kot leno generirane (in potencialno neskončni) strukture. Zato je praktično uvajati dodatni argument-predikat (npr. eop?, kjer “eop” pomeni “end-of-stream”) ki eksplicitno preveri, ali smo dosegli konec toka. S tem argumentom lahko natančno določimo pogoje za prekinitev rekurzije, ne glede na to, kako je tok internt predstavljen.
  
  // TODO: verify
3. (3t) Zapišite definicijo smiselne funkcije foldX/stream nad tokovi!
```
(define (foldX/stream func acc stop stream)
   (if (= stop 0)
      acc
      (foldX/stream func (func (car stream) acc) (- stop 1) ((cdr stream)))))
```
  Primer uporabe:
```
(define naravna
   (letrec ([get (lambda (x)
                     (cons x (lambda () (get (+ x 1)))))])
      (get 1)))

(foldX/stream + 0 5 naravna)
(* 15 *)
```

NALOGA (5t):

V programskem jeziku Python želimo definirati dekorator flatten, ki bo rezultat funkcije, ki vrača gnezdene sezname, pretvoril v sploščen seznam. Napišite definicijo tega dekoratorja (samo sploščevanje definirajte z rekurzivno funkcijo)!

# Primer pred uporabo dekoratorja
def test():
   return [ 1, ['b','c'], [[1],[2]] ]
test()
>> [1, ['b', 'c'], [[1], [2]]]

# Primer po uporabi dekoratorja
@flatten
def test():
   return [ 1, ['b','c'], [[1],[2]] ]
test()
>>> [1, 'b', 'c', 1, 2]

def flatten(func):
   def inner(*args, **kwargs):
      result = func(*args, **kwargs)

      # Rekurzivna funkcija, ki splošča seznam
      def flatten_recursive(lst):
         flattened = []

         for item in lst:
            if isinstance(item, list):
               flattened.extend(flatten_recursive(item))
            else:
               flattened.append(item)

         return flattened

      return flatten_recursive(result)

   return inner

# Primer uporabe dekoratorja
@flatten
def test():
   return [1, ['b', 'c'], [[1], [2]]]

print(test())  # Izhod: [1, 'b', 'c', 1, 2]

4.4.3 2018/19 3. rok

30. 8. 2019

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vrednotena z označenim številom točk.
Vsako nalogo rešujte v predvidenem prostoru. Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša. Podpišite se na vse liste, ki jih oddate.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 70 minut.

NALOGA (5t):

Pri analizi sistema tipov smo omenili lažno pozitivne primere. V zvezi s tem odgovori na naslednja vprašanja:
1. Kaj so to lažno pozitivni primeri?
  
  Torej: LP
  
  To je program, ki nima napake, vendar ga interpreter/prevajalnik označi/analizira da ima napako.
2. Ali so lažno pozitivni primeri zaželeni ali nezaželeni? Če so zaželeni, zakaj so koristni / če so nezaželeni, zakaj se jim želimo izogniti?
  
  Niso zaželjeni, saj prevajalnik zavrača program, ki bi deloval.
3. Podaj kratek primer lažno pozitivnega primera v poljubnem programskem jeziku in navedi nek drugi programski jezik, v katerem je tvoj podani primer pravilno pozitivni primer.
  
  // TODO:

NALOGA (5t):

V programskem jeziku SML sta podani definicija in sinonim podatkovnih tipov:

datatype 'a triple = Trip of 'a * 'a * 'a       (* trojček treh elementov *)
type struc = {comment:string, data:int triple}  (* trojček, ki mu dodamo še komentar *)

Napiši funkcijo f1 tipa val f1 = fn : struc list * struc list -> int, ki sprejme dva seznama tipa struc list in vrne vsoto sredinskih elementov v trojčku. Primer:

val l1 = [{comment="First", data=Trip(1,|2|bg:gray|,3)},  
          {comment="Second", data=Trip(14,|3|bg:gray|,3000)},  
          {comment="Third", data=Trip(51,|4|bg:gray|,~143)}];
val l2 = [{comment="Fourth", data=Trip(1,|1|bg:gray|,1)},  
          {comment="Fifth", data=Trip(4,|7|bg:gray|,3)},  
          {comment="Sixth", data=Trip(51,|4|bg:gray|,~143)}];

- f1 (l1, l2);
val it = 21 : int    (* ker: 2+3+4+1+7+4 = 21, glej podčrtane/označene elemente *)

Funkcija naj uporablja rekurzivno ujemanje vzorcev do največje možne globine (druge implementacije se vrednotijo manj).

Rešitev:

fun f1 ([], []) = 0
  | f1 ({ data = Trip (_, a, _) } :: xs, []) = a + f1 (xs, [])
  | f1 ([], { data = Trip (_, a, _) } :: ys) = a + f1 ([], ys)
  | f1 ({ data = Trip (_, a, _) } :: xs, { data = Trip (_, b, _) } :: ys) =
         a + b + f1 (xs, ys);

Razlaga:

Base case: Če sta oba seznama prazna, vrnemo 0.
En seznam prazen: Če eden od seznamov vsebuje še elemente, vzamemo sredinski element iz prvega (oziroma drugega) elementa in nadaljujemo rekurzijo.
Oba seznama vsebujeta elemente: V prvi glavi seznama odvzamemo sredinski element a iz trikotnika, v drugi glavi pa sredinski element b. Ti sta seštevana, nato pa se funkcija rekurzivno kliče na repa seznamov.

NALOGA (5t):

V programskem jeziku Racket napiši funkcijo z imenom prozi, ki sprejme funkcijo višjega reda f in zaporedno številko elementa n. Funkcija naj oblikuje podatkovni tok, ki ga tvorijo obljube (promises), ki so izdelane s funkcijo zakasnitve (delay). Obljube v toku čakajo na izračun vrednosti (f 1), (f 2), (f 3) itd. v tem zaporedju. Izjema naj bo n-ti element v toku, ki pa naj bo v obliki že prožene obljube. Predpostaviš lahko, da sta funkciji delay in force že implementirani.

Primer delovanja (za prikaz uporabljamo funkcijo (izpisi n tok) s predavanj, ki izpiše prvih n elementov toka tok:
- Funkciji prozi podamo funkcijo (lambda (x) (* x 3)), ki izračuna trikratnik vhodne spremenljivke. Prozi nam oblikuje tok obljub za izračun vrednosti 3 (f 1), 6 (f 2), 9 (f 3) itd. Zadnji parameter funkcije prozi pove, kateri element naj bo že prožen – v prvem primeru je to 2. element, v drugem primeru pa 4.
```
> (izpisi 5 (prozi (lambda (x) (* x 3)) 2))
{#f . #<procedure>}
{#t . 6}
{#f . #<procedure>}
{#f . #<procedure>}
{#f . #<procedure>}
> (izpisi 5 (prozi (lambda (x) (* x 3)) 4))
{#f . #<procedure>}
{#f . #<procedure>}
{#f . #<procedure>}
{#t . 12}
{#f . #<procedure>}
```
Rešitev:
```
(define (prozi f n)
   (define (pripravi-promise i)
      (let ((p (delay (f i))))
         (if (= i n)
            (begin
               (force p)  ; že prožimo obljubo, če je i enak n
               p)
            p)))
   (define (ustvari-tok i)
      (cons (pripravi-promise i)
            (delay (ustvari-tok (+ i 1)))))
   (ustvari-tok 1))
```
Razlaga:
- pripravi-promise: Za dano število i ustvari promise z delay (f i). Če je i enak podanemu n, promise takoj “prožimo” z force, kar povzroči, da bo obljuba v spremenjenem stanju (tako da se ob izpisu pokaže {#t . vrednost}).
- ustvari-tok: Rekurzivno gradi podatkovni tok (stream), kjer je glava tok pripravi-promise i, rep pa se gradi z zakasnitvijo preko delay.
Klic funkcije (prozi (lambda (x) (* x 3)) 2) na primer ustvari tok, kjer bo 2. element že prožen (na izpisu se pokaže {#t . 6}), preostali elementi pa bodo še zakasnili.

NALOGA (5t):

V programskem jeziku Python sta podani naslednji definiciji spremenljivke in funkcije:

d=5
def f1(b):
   def f2(a, b=b, c=d):
      return a+b+c
   return f2

V Pythonu nato izvedemo spodnje zaporedje klicev. Podaj odgovore Pythona (zapiši na črto) posameznih klicev (upoštevaj, da gre za zaporedje):

>>> f1(7)(2)
____
>>> f1(7)(2,3)
____
>>> f1(7)(2,3,4)
____
>>> d=10
>>> f1(7)(2)
____
>>> f1(7)(2,3)
____
>>> f1(7)(2,3,4)
____

>>> f1(7)(2)
14 # 2 + 7 + 5
>>> f1(7)(2,3)
10 # 2 + 3 + 5
>>> f1(7)(2,3,4)
9 # 2 + 3 + 4
>>> d=10
>>> f1(7)(2)
19 # 2 + 7 + 10
>>> f1(7)(2,3)
15 # 2 + 3 + 10
>>> f1(7)(2,3,4)
9 # 2 + 3 + 4

Kakšen doseg vrednosti privzeto uporablja Python (od dveh, ki smo ju omenili na predavanjih)?

Dinamični doseg.

Katera vrsta dosega ima prednosti pred drugo-slabšo? Naštej tri prednosti:

Vrsta dosega: ____

Prednosti:

_____.
_____.
_____.

Vrsta dosega: Leksikalni doseg je boljši kot dinamični doseg.

Prednosti:

neodvisnost lokalnih spremenljivk od zunanjega okolja
neodvisnost funkcije od argumentov
tip funkcije lahko določimo ob njeni deklaraciji

4.4.4 2018/19 1. kolokvij

23. 11. 2018

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 5 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 50 minut.

NALOGA (5t):

Določi podatkovni tip naslednje funkcije. Pri zapisu podatkovnega tipa minimiziraj število oklepajev (torej, zapiši podatkovni tip, kot bi ga izpisal SML v REPL):
```
fun f ({g=g,h=h}, [i,j]) k = 
  if valOf i 
  then fn x => g (k+x) 
  else fn x => h (k-x) ^ "nil" 
```
```
val f = fn: {g:int -> string, h:int -> string} * bool option list -> int -> int -> string
```
Razlaga:
- Prvi parameter je par, kjer je prvi element zapis {g=g, h=h}. Funkciji g in h morata biti tipa int -> string (ker se kličejo z argumentom k (tipa int) in njihovo vrednost se uporabi pri string operacijah).
- Drugi element para je seznam oblike [i, j]. Ker se na i kliče valOf in mora vrednost biti bool, sta tako i kot j tipa bool option.
- Funkcija nato sprejme še parameter k tipa int in vrne funkcijo, ki prav tako sprejme int in vrne string.

NALOGA (5t):

Podan je naslednji podatkovni tip:

datatype pot = Left of pot | Right of pot  
               | Up of pot | Down of pot | start

Zapiši funkcijo tipa:

val coordinate = fn : pot -> {x:int, y:int}

ki za podano pot izpiše koordinato, kam nas pripelje. Pri tem predpostavi, da začnemo v izhodišču {x=0, y=0} in da premik navzgor poveča koordinato y za 1, premik navzdol zmanjša koordinato y za 1, premik v desno poveča koordinato x za 1, premik v levo pa zmanjša koordinato x za 1. Primer klica:

- coordinate (Left (Up (Up (Left (Down (Right start))))));
val it = {x=~1,y=1} : {x:int, y:int}

Pri nalogi uporabi lokalno okolje povsod, kjer je to primerno.

Rešitev:

fun coordinate chain =
   let
      fun pomozna chain2 {x, y} =
         case chain2 of
            start => {x=x, y=y}
            | Left rest => pomozna rest {x=x-1, y=y}
            | Right rest => pomozna rest {x=x+1, y=y}
            | Up rest => pomozna rest {x=x, y=y+1}
            | Down rest => pomozna rest {x=x, y=y-1}
   in
      pomozna chain {x=0, y=0}
   end;

NALOGA (5t):

Podane so naslednje funkcije:
```
fun f1 c l1 l2 = if     c then SOME (l1,l2) else NONE 
fun f2 c l1    = if     c then      l1      else 0 
fun f3 c l1    = if not c then SOME l1      else NONE 
```
(funkcije so poravnane s presledki zaradi večje preglednosti, kateri deli njihove strukture so enaki)

Naloga:
1. Zapiši posplošeno funkcijo višjega reda general (refaktoriziraj programsko kodo), ki lahko nadomesti zgornje tri funkcije. V posplošeni funkciji parametriziraj samo tiste dele, pri katerih so prisotne razlike med zgornjimi funkcijami (in ne celih desnih strani funkcij ali njihovih večjih delov).
```
fun general ifX thenX elseX = if ifX then thenX else elseX
```
1. Zapiši funkcije f1short, f2short in f3short, ki aplicirajo posplošeno funkcijo general tako, da imajo enako delovanje kot prvotne funkcije f1, f2 in f3.
```
fun f1short c l1 l2 = general c       (SOME (l1,l2)) NONE
fun f2short c l1    = general c       l1             0
fun f3short c l1    = general (not c) (SOME l1)      NONE
```
NALOGA (5t):

Implementiraj funkcijo filter izključno z uporabo vgrajene funkcije List.foldl/foldr kot njeno delno aplikacijo. Pri aplikaciji se izogni uporabi operatorja za stikanje seznamov (@).
```
fun filter pogoj seznam =
   List.foldr (fn (x, acc) => if pogoj x
                              then x::acc
                              else acc)
              []
              seznam;
```
Pojasnilo:
- Uporaba List.foldr:
  
  Z uporabo foldr zagotovimo, da ostane vrstni red elementov nespremenjen, saj foldr začne iz zadnjega elementa in gradi rezultat levo proti začetku seznama.
- Preverjanje pogoja in gradnja rezultata:
  
  Za vsak element x se preveri pogoj pogoj x. Če je rezultat true, se x doda na začetek akumulatorja (acc), sicer se akumulator pusti nespremenjen.
- Izogibanje uporabe operatorja @:
  
  Rešitev zgoraj ne uporablja operatorja @ (ki združuje sezname). Namesto tega elemente dodaja neposredno v akumulator s pomočjo operatorja ::.

4.4.5 2018/19 2. kolokvij

18. 1. 2019

S sabo imate lahko 1 A4 list papirja z zapiski, druga literatura ni dovoljena.
Vsaka naloga je vredna 5 točk. Vsako nalogo rešujte v predvidenem prostoru.
Če rešitev rešite na pomožni list, jasno označite, na katero nalogo se nanaša.
Podpišite se na vse liste, ki jih oddate.
Iz vaše rešitve mora biti viden postopek reševanja.
Na vprašanja odgovarjajte kratko (največ 2 povedi), daljši odgovori štejejo 0 točk.
Čas pisanja je 70 minut.

NALOGA (5t):

V programskem jeziku Racket definiraj funkcijo maptok, ki preslika vsak element izvornega toka z uporabo funkcije f. Funkcija naj se torej obnaša podobno kot funkcija map, le da map deluje na seznamih, maptok pa na tokovih.
```
> (define naravna  
      (letrec ([f (lambda (x) (cons x (lambda () (f (+ x 1))))]) 
            (f 1))) 

> (define novi (maptok (lambda (x) (+ x 10)) naravna)) 
> novi 
'(11 . #<procedure>) 
> ((cdr novi)) 
'(12 . #<procedure>) 
> ((cdr ((cdr novi)))) 
'(13 . #<procedure>) 
```
```
(define (maptok f tok)
(cons (f (car tok))
      (lambda () (maptok f ((cdr tok))))))
```
Razlaga:
- Funkcija maptok sprejme funkcijo f in tok tok.
- car tok predstavlja prvi element toka, ki ga preslikamo s funkcijo f.
- cdr tok je funkcija (lambda izraz), ki ko jo pokličemo z ((cdr tok)), vrne rep toka.
- S pomočjo rekurzije preslikujemo tudi rep toka: (lambda () (maptok f ((cdr tok)))).
NALOGA (5t):

V programskem jeziku SML je podan naslednji modul za delo s skladom (stack, LIFO):
```
structure Stack = 
struct 
   exception StackEmpty

   val stack: int list ref = ref [] 

   fun push x = 
      stack := (x::(!stack)) 

   fun pop () = 
      case !stack of 
         [] => raise StackEmpty 
         | g::r => (stack := r; g) 

   fun isEmpty () = 
      !stack = []  
end 
```
1. Zapiši primer uporabe zgornjega modula, ki lahko povzroči nepravilno delovanje sklada.
  Vmodul Stack vsebuje notranjo (mutable) spremenljivko stack, ki je javno dostopna znotraj modula. Tako lahko uporabnik nezadržano poseže vanjo in s tem krši abstrakcijo. Na primer:
```
(* Uporaba modula Stack brez skritja notranje implementacije *)
open Stack;

(* Uporabimo predvidene funkcije *)
push 10;
push 20;
val a = pop ();  (* pričakujemo, da vrne 20 *)

(* Nepravilna uporaba: neposredna manipulacija z notranjim stanje sklada *)
stack := [5, 6, 7];  
(* Zdaj smo popolnoma prepisali stanje sklada *)

(* Nadaljujemo z uporabo operacij *)
push 30;
val b = pop ();  (* rezultat ni več v skladu s pričakovanjem, saj smo zamenjali interno predstavitev *)
```
  V tem primeru uporabnik neposredno spreminja globoko implementacijo (spremenljivko stack), kar lahko povzroči, da sklad ne deluje kot LIFO, kot je pričakovano.
2. Zapiši podpis za zgornji modul, s katerim se lahko izognemo nepravilnemu delovanju.
  Z uporabo podpisa (signature) lahko omejimo, katere komponente so dostopne uporabniku. Namesto, da bi razkrili implementacijske podrobnosti (npr. spremenljivko stack), v podpisu navedemo le:
  - izjemo,
  - funkcije za delo s skladom (push, pop, isEmpty).
  Primer podpisa:
```
signature STACK =
sig
   exception StackEmpty           (* Izjema, ki se sproži, če skušamo izprazniti prazen sklad *)

   val push   : int -> unit       (* Dodajanje elementa na sklad *)
   val pop    : unit -> int        (* Odstranjevanje in vračanje elementa s sklada *)
   val isEmpty: unit -> bool       (* Preverjanje, ali je sklad prazen *)
end
```
  Z uporabo tega podpisa se notranja implementacija (tip in vsebina stack) skrije pred uporabnikom, kar prepreči zunanji vpliv in s tem napake.
  
  // TODO: is probably wrong
3. Ali ste pri odgovoru na prejšnje vprašanje uporabili postopek abstrakcije podatkovnega tipa? Če da – kako in kje? Če ne, zakaj ne?
  Da.
  
  Kako in kje?
  - S podpisom STACK smo uporabniku na razmeroma visoki ravni omogočili operacije, ki so dovolj za delo s skladom, medtem ko smo skrili konkretno implementacijo (tj. tip int list ref in spremenljivko stack).
  - S tem preprečimo, da bi uporabnik neposredno dostopal do notranjega stanja modula in ga spreminjal (kot je prikazano v delu a).
  - To je klasičen primer abstrakcije podatkovnega tipa – uporabniku zagotovimo le vmesnik, medtem ko implementacijske podrobnosti ostanejo skrite, kar povečuje varnost in zanesljivost modula.
  // TODO: is probably wrong
NALOGA (5t):

V programskem jeziku SML je podan naslednji podatkovni tip, ki uporablja vzajemno rekurzijo:
```
datatype sequenceA = A of (int * sequenceB) 
     and sequenceB = B of (int * sequenceB) | C of sequenceA | fin 
```
Z njim lahko oblikujemo izraze, kot je na primer naslednji:
```
val exam1 = A (3, B(5, B(4, |C(A (3, B(1, B(2, fin ))))|bg:gray|)); 
```
- (konstruktor C (siva barva) je namenjen rekurzivnemu gnezdenju izraza istega tipa – lahko se večkrat ponovi)
Napiši funkcijo checkA, ki preveri, ali podani izraz ustreza pogoju, da za vsak podizraz, ki se prične s konstruktorjem A, velja, da je prvi parameter konstruktorja A enak vsoti vseh vrednosti vgnezdenih konstruktorjev B (drugi parameter konstruktorja A). Primer:
- ```
- checkA (A (|3|bg:yellow|, B(|5|bg:yellow|, B(|4|bg:yellow|, C(A (|3|bg:green|, B(|1|bg:green|, B(|2|bg:green|, fin ))))))); 
val it = false : bool 
```
  ima vrednost false, ker: 3!=5+4 (čeprav velja 3=1+2!)
- ```
- checkA (A (|3|bg:yellow|, B(|1|bg:yellow|, B(|2|bg:yellow|, C(A (|15|bg:green|, B(|5|bg:green|, B(|13|bg:green|, fin ))))))); 
val it = true : bool 
```
  ima vrednost true, ker: 3=1+2 in 15=5+13
Namig: Uporabi vzajemno rekurzijo.

Rešitev:
```
(* Definicija funkcij z vzajemno rekurzijo: *)
fun checkA (A(n, sB)) =
   let
      val (sumB, validB) = checkB sB
   in
      (n = sumB) andalso validB
   end
and checkB fin = (0, true)
  | checkB (B(x, sb)) =
      let
         val (s, valid) = checkB sb
      in
         (x + s, valid)
      end
  | checkB (C(a)) = (0, checkA a);
```
Pojasnilo:
- Pri zapisu A(n, sB):
  - Funkcija checkB preleti parameter sB (tipa sequenceB) po naslednjem pravilu:
    - Če je sB enak fin, vrne (0, true).
    - Če je sB zapis B(x, sb), nato rekurzivno obdelamo sb in prištejemo x k seštevku.
    - Če je sB zapis C(a), to pomeni, da se pojavi podizraz tipa A. V tem primeru se seštevek vrednosti na trenutnem nivoju zaključi (vrnemo 0) in rekurzivno preverimo podizraz s funkcijo checkA.
- Funkcija checkA preveri, da je število n enako seštevku dobljenem iz sB in hkrati da so vsi nadaljnji (pod)izrazi pravilni.

NALOGA (5t):

V programskem jeziku Python napiši dekorator delay, ki zakasni izvajanje podane funkcije. Dekorator naj funkcijo f ovije v generator, ki ob vsakem klicu metode __next__() vrne rezultat funkcije. Ob prvem klicu naj se dejansko izvede evalvacija funkcije, ob vseh naslednjih pa naj se vrača njen shranjen rezultat. Generator naj torej deluje podobno kot princip zakasnitve in sprožitve (delay in force) v jeziku Racket.

Na primer, če definiramo:

@delay
def kvadrat(x):
   return x*x

naj se funkcija kvadrat obnaša na naslednji način:

k = kvadrat(5)
k
<generator object delay.<locals>.wrapper at 0x032116F0>
k.__next__()            # tukaj Python dejansko izvede evalvacijo funkcije
25
k.__next__()            # samo vrne shranjen rezultat
25
k.__next__()            # samo vrne shranjen rezultat
25

Rešitev:

def delay(func):
   def wrapper(*args, **kwargs):
      def generator():
         result = func(*args, **kwargs)  # Izvedba funkcije ob prvem klicu __next__()
         yield result
         while True:
            yield result           # Vsak naslednji klic vrne isti rezultat
      return generator()
   return wrapper

\(A \land 0 \sim 0\)	\(A \lor 0 \sim A\)	\(A = 0 \sim \neg A\)	\(A \Rightarrow 0 \sim \neg A\)
\(A \land 1 \sim A\)	\(A \lor 1 \sim 1\)	\(A = 1 \sim 1\)	\(A \Rightarrow 1 \sim A\)
\(A \land 1 \land 1 \sim A\)	\(A \lor 0 \lor 0 \sim A\)	\(0 = A \sim 1\)	\(\neg 0 \sim 1\)
\(A \land 1 \land 0 \sim 0\)	\(A \lor 0 \lor 1 \sim 1\)	\(1 = A \sim A\)	\(\neg 1 \sim 0\)